Algorithme du Doomsday
Permet de trouver de tête le jour de la semaine pour n’importe quelle date du calendrier grégorien (à partir de 1753).
On donne une date sous la forme $jour/mois/annee$.
On décompose tout d’abord $annee$ en $s\times 100 + an$ où $s$ est le nombre de siècles ($an<100$).
doomscentury $c$
- on calcule le reste de la division euclidienne par 4 du nombre de siècle $s$
- on multiplié par 2
- on prend le complément à 7
$$c = 7-(s\mod 4) \times2 $$
doomsyear $y$
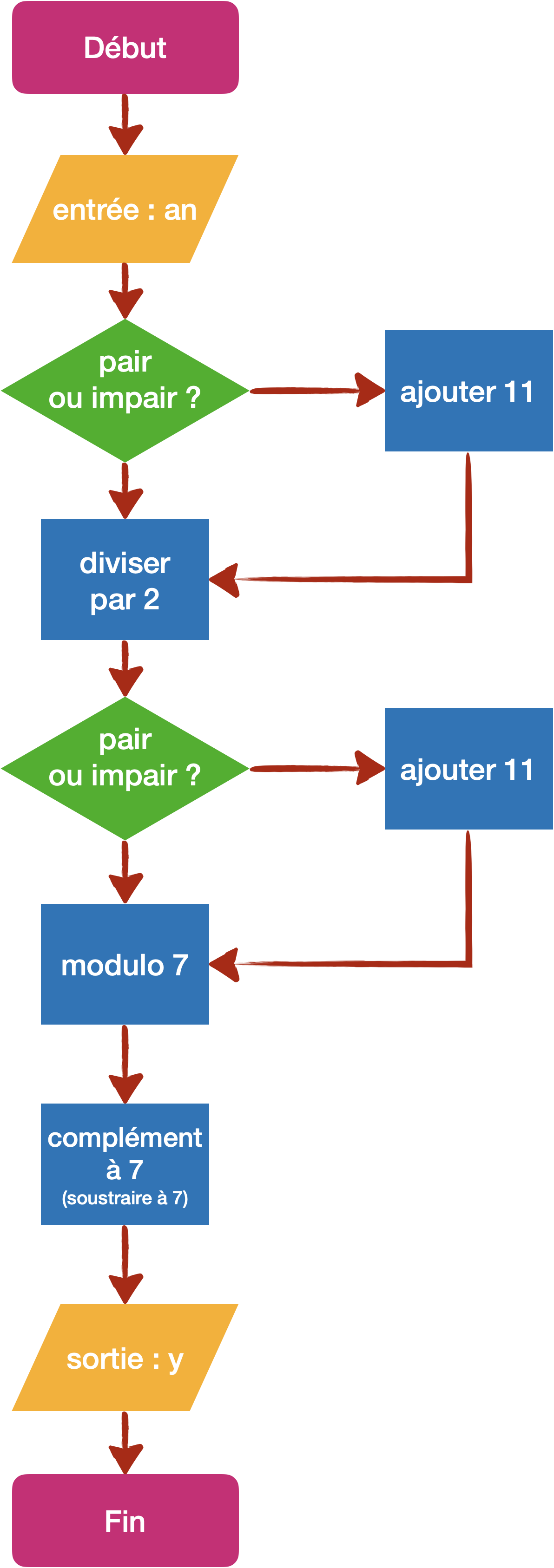
Doomsday1
On calcule $c+y\mod 7$
Cela donne le Doomsday de l’année :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| mardi | mercredi | jeudi | vendredi | samedi | dimanche | lundi |
doomsday1 $d$
Liste des doomsday $d$/$mois$ pour une année non bissextile :
| 31/1 | 28/2 | 7/3 | 4/4 | 9/5 | 6/6 | 11/7 | 8/8 | 5/9 | 10/10 | 7/11 | 12/12 |
|---|
Pour une année bissextile, on ajoute 1 à $d$ pour les 2 premiers mois : 32/1 et 29/2
Aide mémoire :
janvier et février : dernier jour du mois (+1 si bissextile)
tous les mois pairs : $x/x$ ($\Rightarrow d=mois$)
mars, mai, juillet : $x+4/x$ ($\Rightarrow d=mois+4$)
septembre, novembre : $x-4/x$ ($\Rightarrow d=mois-4$)
Plus qu’à faire la différence entre $jour$ et le doomsday du mois $d$ modulo 7 : $jour-d\mod 7$
Si le résultat est négatif, on ajoute 7.
Puis on ajoute au Doomsday pour trouver le jour de la semaine.
Exemples
Quel jour de la semaine tombe le 27/1/3252 ?
-
doomscentury :
$s=32$
$c = 7-(32 \mod 4)\times 2 = 7$
-
doomsyear :
- 52 est pair $\rightarrow 52/2=26$
- 26 est pair $\rightarrow 26\mod7 = 5$
- $y = 7-5=2$
-
Doomsday :
$(c+y)\mod7 = 2\rightarrow$ jeudi
0 1 2 3 4 5 6 jeudi vendredi samedi dimanche lundi mardi mercredi -
doomsday :
3252 est une année bissextile donc le doomsday $d$ de janvier est 32.
$(27-32)\mod 7=-5$ et $-5+7=2$
Conclusion : le 27/1/3252 est un samedi.
Quel jour de la semaine tombe le 17/11/1921 ?
-
doomscentury :
$s=19$
$c=7-(19\mod4)\times 2=1$
-
doomsyear :
- 21 est impair $\rightarrow (21+11)/2=16$
- 16 est pair $\rightarrow 16\mod7=2$
- $y=7-2=5$
-
Doomsday :
$(c+y)\mod7=6\rightarrow$ lundi
0 1 2 3 4 5 6 lundi mardi mercredi jeudi vendredi samedi dimanche -
doomsday :
en novembre $d=7$
$(17-7)\mod7=3$
Conclusion : le 17/11/1921 tombe un jeudi.
Entraînement
Projet
Reproduire le programme d'entraînement ci-dessus.
Une solution :
from random import randint
from time import time
nb_tent = 0
tps_moy = 0
nb_echecs = 0
def Doomsday(jour,mois,annee):
doomsday = {i:i for i in range(3,13)}
if bissextile:
doomsday[1] = 32
doomsday[2] = 29
else:
doomsday[1] = 31
doomsday[2] = 28
for m in doomsday.keys():
if m%2:
if m in (3,5,7):
doomsday[m] += 4
elif m in (9,11):
doomsday[m] -= 4
doomcentury = (7 - ((annee // 100) % 4) * 2) % 7
an = annee-annee//100*100
if an % 2:
an += 11
an //= 2
if an % 2:
an += 11
an %= 7
doomyear = 7 - an
ecart = (jour - doomsday[mois])
signe = ""
if ecart > 0:
signe = "+"
ecart %= 7
fin = (ecart + doomcentury + doomyear) % 7
return signe,fin,ecart,doomcentury,doomyear,doomsday
tps_min = 100
tps_max = 0
liste_jours = ["mardi","mercredi","jeudi","vendredi","samedi","dimanche","lundi"]
while True:
y = randint(1753,2150)
m = randint(1,12)
mois_cts = (4,6,9,11)
bissextile = False
if y%4 == 0 and y%400 not in (100,200,300):
bissextile = True
if m == 2:
if bissextile:
d = randint(1,29)
else:
d = randint(1,28)
elif m in mois_cts:
d = randint(1,30)
else:
d = randint(1,31)
print("date :")
date = "| {}/{}/{} |".format(d,m,y)
print("-"*len(date))
print(date)
print("-"*len(date))
start = time()
int_j = input("Choisir le jour de la semaine (de 1 à 7) : ")
chiffres = list(map(str,range(1,8)))
while int_j not in chiffres:
int_j = input("saisie non valide, recommencez : ")
int_j = int(int_j)
end = time()
print("temps mis : {:.1f} s\n".format(end-start))
signe,fin,ecart,doomcentury,doomyear,doomsday = Doomsday(d,m,y)
nb_tent += 1
jour = liste_jours[fin].upper()
if (fin+1)%7+1==int_j:
print("Bien joué !")
else:
print("Echec...")
nb_echecs += 1
print("-"*(len(jour)+4))
print("| {} |".format(jour))
print("-"*(len(jour)+4))
print("\nCalculs :")
print("-"*9)
print("doomcentury = {}".format(doomcentury))
print("doomyear = {}".format(doomyear))
n = (doomyear + doomcentury) % 7
print("=> Doomsday en {} = {}".format(y,liste_jours[n]))
print("écart par rapport au doomsday du mois ({}/{})".format(doomsday[m],m))
if bissextile and m in (1,2):
print("(année bissextile)")
print("{}{} jours".format(signe,ecart))
tps = end-start
tps_moy += tps
if tps < tps_min:
tps_min = tps
if tps > tps_max:
tps_max = tps
rep = input("\nTaper q pour arreter, Entree pour continuer\n")
if rep == "q":
pourcent = nb_echecs/nb_tent*100
tps_moy = tps_moy/nb_tent
print("\nSTATS :")
print("-"*7)
print("nombre de tentatives : {}".format(nb_tent))
print("pourcentage d'erreurs : {:.0f}%".format(pourcent))
print("temps moyen : {:.1f} s".format(tps_moy))
print("temps max : {:.1f} s".format(tps_max))
print("temps min : {:.1f} s".format(tps_min))
break
Code suivant une méthode un poil plus efficace :
while True:
date = input("Quelle date ? (format JJ/MM/AAAA) :\n")
slash = []
for i,c in enumerate(date):
if c == "/":
slash.append(i)
jour, mois, annee = int(date[:slash[0]]),int(date[slash[0]+1:slash[1]]),int(date[slash[1]+1:])
if annee > 1600:
break
else:
print("Le calendrier Grégorien ne commence qu'en septembre 1752, choisir une date au-delà.")
liste_jours = ["mardi","mercredi","jeudi","vendredi","samedi","dimanche","lundi"]
Doomsday = {i:i for i in range(3,13)}
if annee%4 == 0 and annee%400 not in (100,200,300):
print("année bissextile")
Doomsday[1] = 32
Doomsday[2] = 29
else:
Doomsday[1] = 31
Doomsday[2] = 28
for m in Doomsday.keys():
if m%2:
if m in (3,5,7):
Doomsday[m] += 4
elif m in (9,11):
Doomsday[m] -= 4
print(f"liste des doomsday pour {annee} :")
joursdoom = []
for (k,v) in Doomsday.items():
joursdoom.append((k,v))
joursdoom.sort()
for e in joursdoom:
m,j = e
print(f"{j}/{m}")
# Détermination du Doomsday
doomcentury = (7 - ((annee//100)%4) * 2) % 7
print(f"{doomcentury = }")
ans = annee-annee//100*100
#doomyear = ans//12+ans%12+ans%12//4
if ans%2:
ans += 11
ans //= 2
if ans%2:
ans += 11
ans %= 7
doomyear = 7-ans
print(f"{doomyear = }")
n = (doomyear+doomcentury)%7
print(f"Doomsday en {annee} = {liste_jours[n]}")
ecart = (jour-Doomsday[mois])
print(f"écart par rapport au doomsday du mois ({Doomsday[mois]}/{mois})")
signe = ""
if ecart > 0:
signe = "+"
print(f"{signe}{ecart} jours")
ecart %= 7
fin = (ecart+doomcentury+doomyear)%7
print("=>",liste_jours[fin].upper())