TP 0 : Démarrage
Cliquez sur cette invitation pour récupérer le repository du TP.
Exo 1
Combien de fois une feuille de papier d’épaisseur $e=0,1$ mm doit-elle être pliée pour atteindre la Lune ?
Écrivez dans la cellule suivante un code permettant d’obtenir la réponse. Le plus simple est d’utiliser une boucle
while.
Wolfram alpha vous donne avec précision la distance Terre-Lune.
### VOTRE CODE
Correction (cliquer pour afficher)
e = 0.1e-3 D_TL = 385e6 ep_tot = e nb_plis = 0 while ep_tot < D_TL: nb_plis += 1 ep_tot *= 2 print(nb_plis)
Dans la cellule suivante, affectez à la variable
nb_plisla valeur entière trouvée.
nb_plis = 0
Correction (cliquer pour afficher)
42
Exo 2
Complétez le code de la fonction
palindromepour qu’il retourne un booléen valantTruesi la chaîne de caractères passée en argument est bien un palindrome etFalsesinon.
def palindrome(chaine):
"""
palindrome(chaine: string) -> test: bool
précondition: chaine est une chaine de caractères
postcondition: si chaine est un palindrome, test vaut True, et False sinon.
"""
### VOTRE CODE
return test
Correction (cliquer pour afficher)
def palindrome(chaine): test = chaine == chaine[::-1] return test
Exo 3
Une liste peut être utilisée comme une représentation simple d’un polynôme, $P(x)$, où les éléments sont les coefficients des puissances de $x$ successives et les indices sont les puissances elles-mêmes. Ainsi le polynôme
$P(x)=3+6x+2x^3$ sera représenté par la liste [3,6,0,2].
L’exécution du code de la cellule suivante ne donne pas le résultat attendu. Il est sensé donné la liste représentant le polynôme dérivé $P’(x)$.
Corrigez-le afin de rendre le retour affiché correct.
P = [3, 6, 0, 2]
dPdx = []
i = 0
for c in P:
i += 1
dPdx.append(i*c)
dPdx
[3, 12, 0, 8]
Correction (cliquer pour afficher)
Il suffit de parcourir les éléments de $P$ en sautant le premier.
Pour cela, on peut remplacerfor c in P:parfor c in P[1:]:.
On obtient bien alors[6,0,6].
Exo 4
L’algorithme de Luhn est une formule de somme de contrôle permettant de valider un numéro de carte bancaire. On considère le numéro de carte comme une suite de nombres à 1 chiffre.
- Renverser la liste.
- Prendre tous les chiffres en position paire dans la liste renversée (2e chiffre, 4e chiffre, etc.) et doubler leur valeur, si le résultat dépasse 10, on ajoute les deux chiffres du résultat (par exemple 6→12→3).
- Sommer tous les nombres de la nouvelle liste (les modifiés et les non-modifiés)
- Si cette somme vaut 0 modulo 10. Le numéro de carte est valide.
Compléter la fonction suivante permettant de vérifier un numéro de carte.

def verifcarte(numero):
"""
verifcarte(numero: string) -> bool
précondition: numéro est une chaîne de caractères (par exemple '1205 1205 1205 1205')
postcondition: la fonction retourne vrai si le numéro est valide et faux sinon
"""
num = ''
for c in numero:
if c in '0123456789':
num += c # permet de sauter les espaces ou tirets
assert len(num)==16, 'Le numéro ne contient pas 16 chiffres'
### VOTRE CODE
Correction (cliquer pour afficher)
def verifcarte(numero): num = '' for c in numero: if c in '0123456789': num += c assert len(num)==16, 'Le numéro ne contient pas 16 chiffres' num_1 = num[::-1] num_2 = '' for i in range(1,len(num_1),2): p = int(num_1[i])*2 if p < 10: num_2 += str(p) else: s = int(str(p)[0])+int(str(p)[1]) # cela revient à faire p-9 num_2 += str(s) S = 0 for c in num_2: S += int(c) if S%10 == 0: return True else: return False
# Pour tester votre fonction
num = '0000 0000 0000 9258'
verifcarte(num)
Exo 5
La suite de Syracuse est une suite d’entiers naturels définie de la manière suivante :
on part d’un nombre entier plus grand que zéro ;
- s’il est pair, on le divise par 2 ;
- s’il est impair, on le multiplie par 3 et on ajoute 1.
En répétant l’opération, on obtient une suite d’entiers positifs dont chacun ne dépend que de son prédécesseur.
Lorsque 1 est atteint, un cycle de longueur 3 se répète sans fin : 1, 4, 2, 1, 4, 2, 1,…
On ajoute donc une nouvelle règle :
- si 1 est atteint, la suite s’arrête.
Appelons temps de vol le nombre de termes de la suite.
Construisez une fonction qui renvoie le temps de vol correspondant à une entrée donnée.
def tpsdevol(nombre):
"""
tpsdevol(nombre: int) -> T: int
précondition: nombre est un entier positif
"""
### VOTRE CODE
return T
Correction (cliquer pour afficher)
def tpsdevol(nombre): tps = 0 while nombre != 1: tps += 1 if nombre%2 == 0: nombre //= 2 else: nombre = 3*nombre+1 return tps
La conjecture de Syracuse (ou Collatz) dit que toutes les suites de Syracuse ont une fin.
Confirmons la conjecture pour tous les entiers inférieurs à 100 grâce à votre fonction.
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.figure(figsize=(15,8),dpi=150)
X = [i for i in range(1,100)]
T = []
for x in X:
T.append(tpsdevol(x))
plt.plot(X,T)
plt.xlabel('nombre de départ')
plt.ylabel('temps de vol')
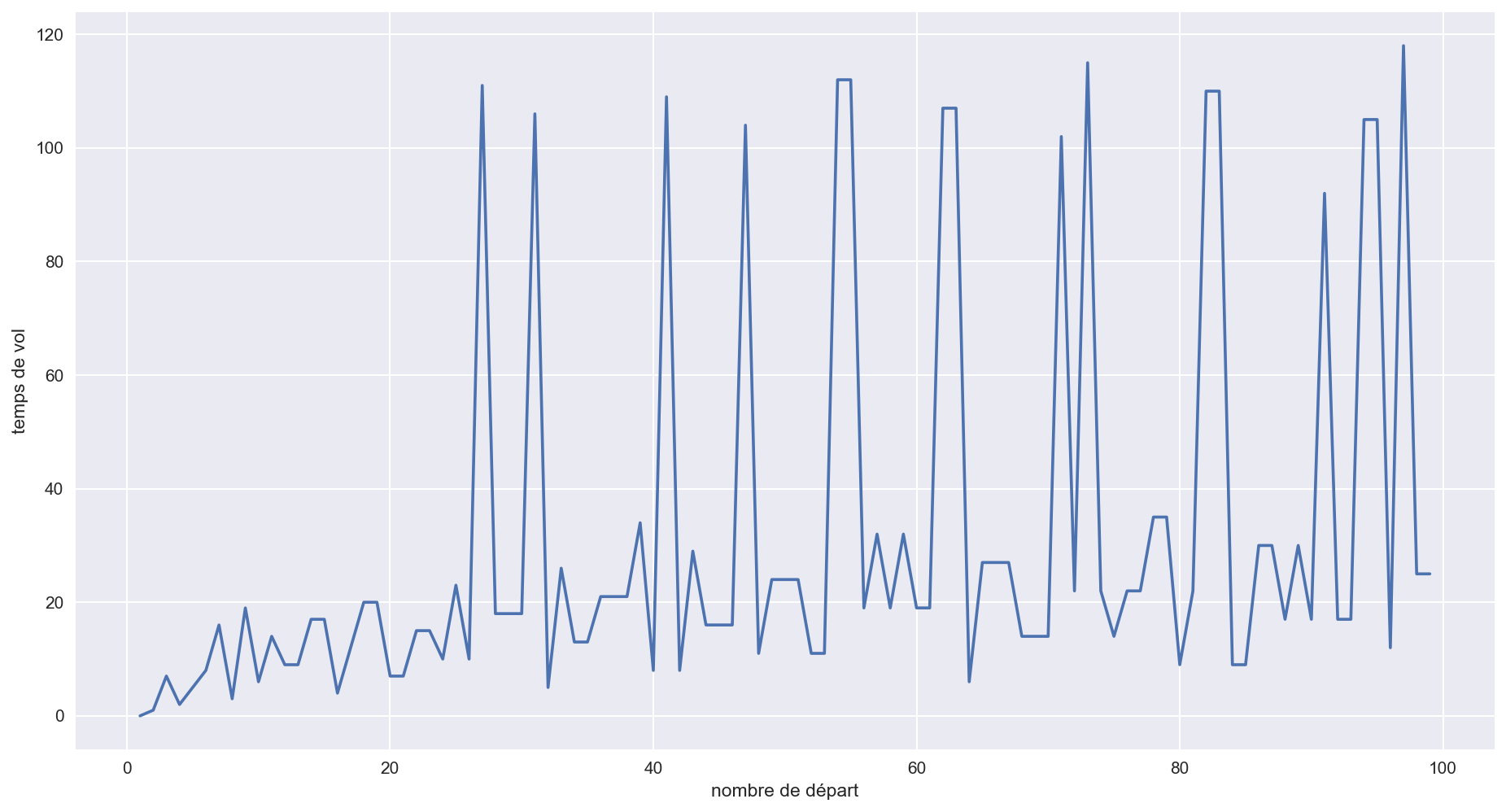
Commentaire (cliquer pour afficher)
Malgré son allure enfantine, la conjecture de syracuse a résisté (et résiste encore aujourd'hui) aux plus brillants mathématiciens ayant essayé de la démontrer.