TP 1 : recherche simple

TP 1 : Recherche séquentielle dans un tableau unidimensionnel. Dictionnaires.

Cliquez sur cette invitation pour récupérer le repository du TP.

Recherche d’un élément dans une liste

Écrire une fonction recherche qui prend pour argument un élément et une liste et qui retourne True si l’élément est présent et False sinon.
Le corps de la fonction devra comprendre une boucle.

Rq : le but de recherche est de reproduire le fonctionnement du mot clé in.

def recherche(x,L):
    '''
    recherche(x: tout type, L: list) -> bool
    '''
    ### VOTRE CODE

Correction (cliquer pour afficher)

def recherche(x,L):
    for e in L:
        if e == x:
            return True
    return False

Dans le pire des cas (élément ne se trouvant pas dans la liste), combien de comparaisons doit-on opérer pour savoir si un élément est présent dans une liste de taille 400 ?

Correction (cliquer pour afficher)

La fonction réalise une comparaison pour chaque élément $\Rightarrow$ 400 comparaisons.

Construisez une fonction dico qui prend en argument une liste L de $n$ entiers inférieurs à $n$ et qui retourne un dictionnaire de longueur $n$ dont les clés sont les $n$ premiers entiers (de 0 à $n$-1) et les valeurs comptent le nombre de fois que la clé est présente dans la liste.
Exemple : s’il y a 2 fois l’élément 18 dans la liste L, alors dico(L)[18]==2, et si l’élément 97 n’est pas présent dans la liste, alors dico(L)[97]==0.

from random import randint 

def dico(L):
    '''
    dico(L: list) -> dict
    précondition: si la longueur de L vaut n, alors L ne contient que des entiers < n
    '''
    ### VOTRE CODE

Correction (cliquer pour afficher)

def dico(L):
    n = len(L)
    dic = {}
    for i in range(n):
        dic[i] = 0
    for e in L:
        dic[e] += 1
    return dic

Commentaire (cliquer pour afficher)

La signature de la fonction et les préconditions délimitent les types et les domaines des entrées (les arguments).
On peut, ou non, s'assurer de leur respect grâce à des asser.
Ici, par exemple, on aurait pu commencer le code de la fonction par les lignes suivantes :
n = len(L)
for e in L:
    assert e < n

Définissons une fonction recherche_dico qui vérifie si un entier est bien présent :

def recherche_dico(e,dic):
    '''
    recherche_dico(e: int, dic: dict) -> bool
    '''
    if dic[e] >= 1:
        return True
    else:
        return False
    
# Exemple d'utilisation:
L = [5,2,3,1,2,0,2]
dic = dico(L)
(recherche_dico(3,dic),recherche_dico(4,dic))

(True, False)

L’intérêt de recherche-dico est d’aller beaucoup plus vite que recherche comme le montre le graphe suivant (l’execution du code peut prendre quelques secondes) :

from time import time
from random import randint
import matplotlib.pyplot as plt
plt.style.use('ggplot')

I, T_ch, T_dico = [], [], []

for i in range(1000,200000,1000):
    L = []
    L = [randint(0,i-1) for k in range(i)] # randint(i,j) retourne un entier dans {i;...;j}
    # la liste L contient i éléments tirés au hasard entre 0 et i-1
    dic = dico(L)                          # on crée un dictionnaire à partir de L grâce à la fonction 'dico'
    element = randint(0,i-1)               # 'element' est un entier tiré au hasard entre 0 et i-1
    start = time()                         # on note l'heure exacte
    recherche(element,L)
    stop1 = time()
    recherche_dico(element,dic)
    stop2 = time()
    T_ch.append(stop1-start)
    T_dico.append(stop2-stop1)
    I.append(i)

plt.figure(figsize = (15,5))
plt.plot(I,T_dico,label="recherche_dico")
plt.plot(I,T_ch,label="votre fonction 'recherche'")
plt.xlabel('taille de la liste')
plt.ylabel("temps d'exécution (s)")
plt.legend()

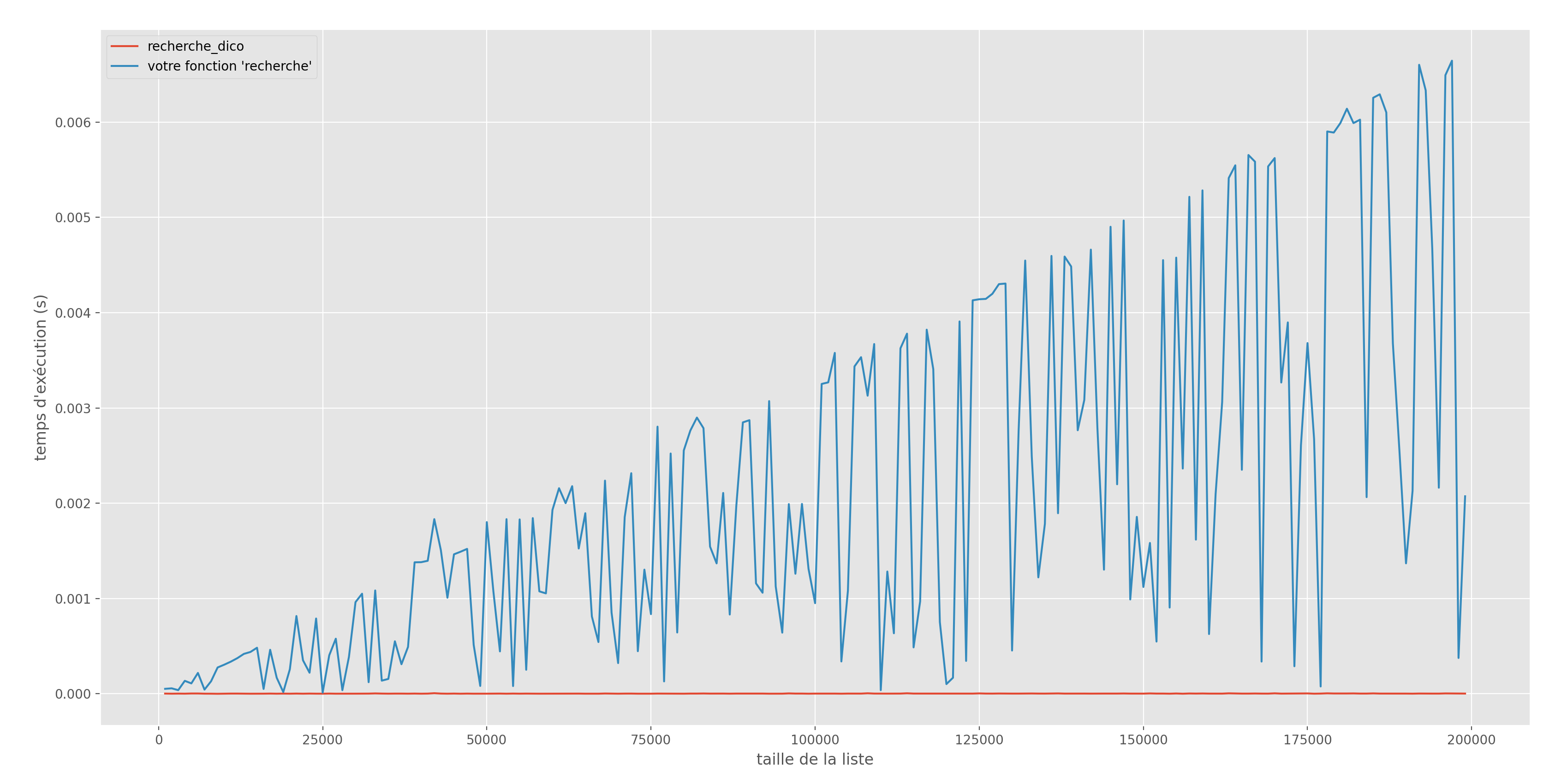
Commentaire (cliquer pour afficher)

Le graphique montre que la fonction recherche a une complexité constante (nombre constant d'opération) dans le meilleur des cas (élément à rechercher au début de la liste) et une complexité linéaire (nombre d'opérations proportionnel à la longueur de la liste) dans le pire des cas.
Par contre, la fonction recherche_dico semble, elle, toujours de complexité constante.

Recherche d’un maximum

Écrire une fonction maximum qui prend pour argument une liste et qui retourne le plus grand élément de la liste.
(Interdiciton d’utiliser la fonction native max évidemment)

def maximum(L) :
    '''
    maximum(L: list) -> float ou int
    '''
    ### VOTRE CODE

Correction (cliquer pour afficher)

def maximum(L):
    m = L[0] 
    for e in L[1:]: # on commence à partir du 2e élément de L
        if e > m:
            m = e
    return m

Commentaire 1 (cliquer pour afficher)

L'utilisation du découpage (slicing) L[1:] permet d'éviter l'erreur indexerror : list index out of range (qui signifie que l'indice est hors-plage) dans le cas d'une liste de seulement 1 élément. En effet, L[1:] ne renvoie alors pas une erreur mais la liste vide []. On ne rentre donc pas dans la boucle.
On aurait aussi pu utiliser L pour itérer car bien que cela entraîne une comparaison supplémentaire inutile, pour des grandes listes, c'est complètement insignifiant.

Rq : la fonction lèvera une erreur si L est une liste vide car dans ce cas, même L[0] n'existe pas.

Commentaire 2 (cliquer pour afficher)

Il faut aussi savoir construire une fonction qui renvoie l'indice du maximum (le premier indice au cas où le maximum serait présent plusieur fois) :
def indice_maximum(L):
    n = len(L)
    im = 0
    for i in range(1,n):
        if L[i] > L[im]:
            im = i
    return im
Et si on a besoin des deux à la fois, on peut renvoyer le max et son indice dans un tuple :
def max_et_indice(L):
    n = len(L)
    im = 0
    m = L[im]
    for i in range(1,n):
        if L[i] > m:
            im = i
            m = L[im]
    return m,im

Que se passera-t-il si on passe la liste suivante [1,3,'a',-2] en argument à maximum ?

maximum([1,3,'a',-2])

Pour éviter cela, vous devrez vous assurez en amont que la liste donnée en argument contient bien que des nombres.
Rappel : type(3) renvoie int et type(2.8) renvoie float.
Vous placerez un assert en début de fonction prévenant l’utilisateur que la liste contient des types farfelus.

def maximum_secure(L) :
    '''
    maximum(L: list) -> float ou int
    la fonction lève une 'AsserionError' si la liste ne contient pas que des nombres
    '''
    ### VOTRE CODE

Correction (cliquer pour afficher)

def maximum_secure(L) :
    for e in L :
        assert type(e)==int or type(e)==float, 'la list ne contient pas que des nombres'
    return maximum(L)

On aurai aussi pu écrire : assert type(e) in (float,int)

Construisez maintenant une fonction max_2 qui retourne le deuxième maximum défini comme le plus grand élément strictement inférieur au maximum (s’il y a plusieurs éléments ayant la valeur maximale, il ne faut pas retourner un de ceux-là).
Votre fonction max_2 devra utiliser votre ancienne fonction maximum, mais vous ferez attention à ne pas placer maximum à l’intérieur d’une boucle.

def max_2(L):
    '''
    max_2(L: list) -> float ou int
    précondition: L est une liste de nombres
    postcondition: la fonction retourne le plus grand élément strictement plus petit que le max de la liste.
    '''
    ### VOTRE CODE

Correction (cliquer pour afficher)

def max_2(L):
    assert len(L)>1, "la liste ne contient qu'un élément"
    x = L[0]
    b = False # b va servir à tester qu'un 2e max est bien présent
    for e in L:
        if e != x:
            b = True
    assert b, "pas de second max puisque tous les éléments sont identiques"
    M = maximum(L)
    m = M
    while m == M:
        L.remove(m)
        m = maximum(L)
    m2 = maximum(L)
    return m2

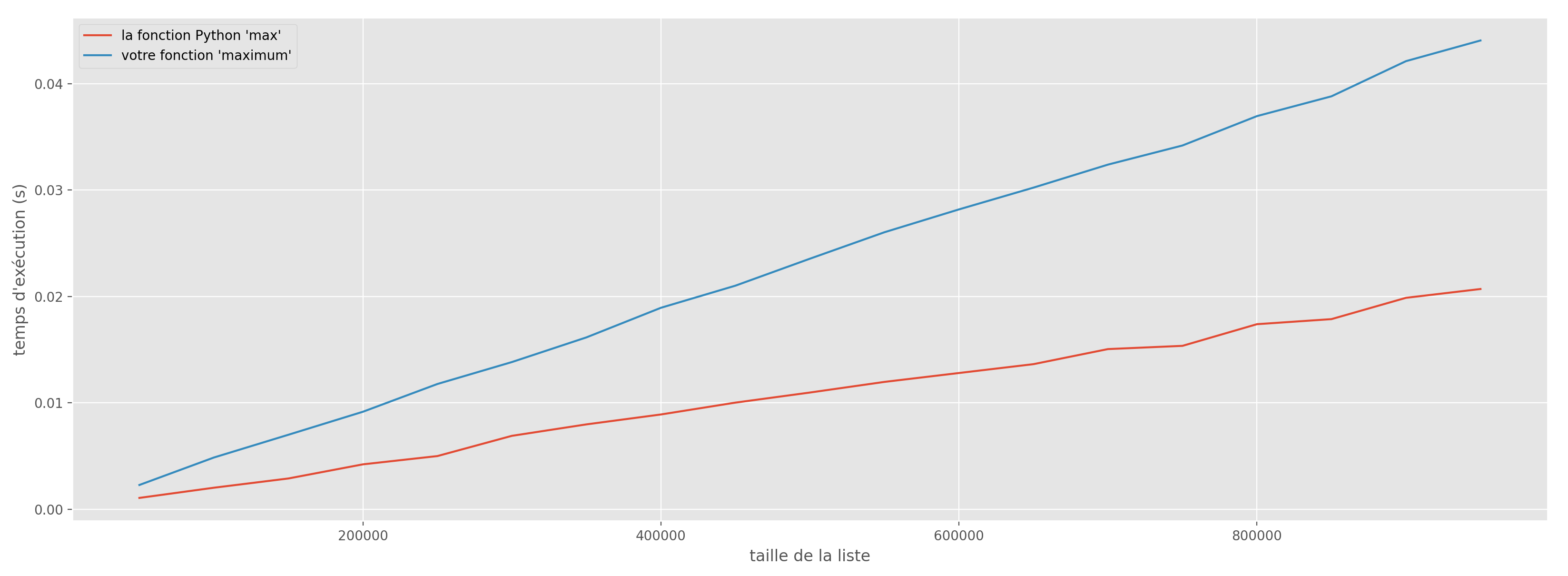
Ci-dessous est représentée l’évolution du temps d’exécution de la fonction native max ainsi que de la fonction maximum (si vous avez réussi à l’implémenter) en fonction de la taille de la liste en argument.
On remarque que cette évolution est linéaire : l’augmentation du temps d’exécution semble proportionnelle à l’augmentation de la taille de la liste.

I, T_max, T_maximum = [], [], []
for i in range(50000,1000000,50000):
    L = []
    for k in range(i):
        L += [randint(0,k)]
        # randint(i,j) retourne un entier dans {i;...;j}
    start1 = time()
    max(L)
    stop1 = time()
    T_max.append(stop1-start1)
    start2 = time()
    maximum(L)
    stop2 = time()
    T_maximum.append(stop2-start2)
    I.append(i)

plt.figure(figsize = (15,5))
plt.plot(I,T_max,label = "la fonction Python 'max'")
plt.plot(I,T_maximum,label = "votre fonction 'maximum'")

plt.xlabel('taille de la liste')
plt.ylabel("temps d'exécution (s)")
plt.legend()

Ajoutez la fonction max_2 à ce graphe et répondre dans la cellule suivante si oui ou non, le temps d’exécution de max_2 semble dépendre linéairement de la taille de la liste.

Correction (cliquer pour afficher)

Code avec ajout de max_2 :

I, T_max, T_maximum, T_max2 = [], [], [], []
for i in range(50000,1000000,50000) :
    L = []
    for k in range(i) :
        L += [randint(0,k)]
        # randint(i,j) retourne un entier dans {i;...;j}
    start1 = time()
    max(L)
    stop1 = time()
    T_max.append(stop1-start1)
    start2 = time()
    maximum(L)
    stop2 = time()
    T_maximum.append(stop2-start2)
    start3 = time()
    max_2(L)
    stop3 = time()
    T_max2.append(stop3-start3)
    I.append(i)
plt.figure(figsize = (15,5))
plt.plot(I, T_max, label= "la fonction Python 'max'")
plt.plot(I, T_maximum, label= "votre fonction 'maximum'")
plt.plot(I, T_max2, label= "votre fonction 'max_2'")
plt.xlabel('taille de la liste')
plt.ylabel("temps d'exécution (s)")
plt.legend()

On obtient :

La fonction max_2 semble donc bien dépendre linéairement de la taille de la liste. La pente plus élevée traduit que le nombre d'opérations à réaliser pour chaque élément de la liste est plus élevé.

Commentaire (cliquer pour afficher)

La fonction python native n'utilise pas un meilleur algorithme. D'ailleurs sa complexité est bien linéaire mais comme souvent avec les fonctions natives, l'optimisation joue sur l'interfaçage entre le code et la machine. Le code d'une fonction native Python n'est pas écrit en Python mais dans un langage de plus bas niveau, le C, plus proche de la machine, donc plus rapide.