Algorithmes opérant sur une structure séquentielle par boucles imbriquées
Cliquez sur cette invitation pour récupérer le repository du TP.
Chercher un mot dans un texte
Écrire une fonction
cherche_motnaïve qui recherche si un mot est présent dans un texte en comparant chaque morceau du texte de la taille du mot au mot recherché.
Vous devrez vous assurez (grâce à des assertions) que le mot et le texte sont bien des chaînes de caractères et que le mot n’est pas plus long que le texte.
def cherche_mot(mot, texte):
'''
cherche_mot(mot: string, texte: string) -> bool
'''
### VOTRE CODE
Correction (cliquer pour afficher)
def cherche_mot(mot,texte): assert type(mot) == str, "'mot' n'est pas une chaîne de caractères" assert type(texte) == str, "'texte' n'est pas une chaîne de caractères" n = len(texte) m = len(mot) assert n >= m, "'mot' plus grand que 'texte'..." for i in range(n-m+1): if texte[i:i+m] == mot: return True return False
Commentaire (cliquer pour afficher)
Imaginez que vous ayez oublié le+1dans lerangede la boucle. Vous devez être capable de déceler l'erreur en testant votre fonction.
Vos tests doivent consister à vérifier que votre fonction donne la réponse attendue sur différents exemples. Et en particulier, il faut toujours tester les extrémités d'un domaîne et les cas pathologiques lorsqu'il y en a (comme une division par zéro).
Ici par exemple, il était capital de tester que la fonction réponde bienTruepour un mot au tout début du texte ou à la toute fin.
Si la fonction bugue, il faut utiliser des
Par exemple, ici, on aurait pu écrireprint(texte[i:i+m])en première ligne de la boucle.
# importation de la classique liste de mots de passe rockyou (cela prend quelques secondes)
from urllib.request import urlopen
url = 'http://cordier-phychi.toile-libre.org/Info/github/rockyou.txt'
rockyou = urlopen(url).read().decode('latin-1')
print(f"Le fichier rockyou contient {len(rockyou.split())} mots de passe !")
Le fichier rockyou contient 14445388 mots de passe !
# vous pouvez tester la présence de votre mot de passe dans la liste
mot_de_passe = '...'
cherche_mot(mot_de_passe,rockyou)
Quel est le nombre minimum de comparaisons à faire pour s’assurer qu’un mot de 3 caractères est absent d’une chaîne de 10 caractères ? Attention, comparer deux mots ne compte pas que pour une seule comparaison !
Correction (cliquer pour afficher)
Pour chaque morceau du texte de la taille du mot, il y a $m$ comparaisons réalisées ($m$ : taille du mot). Ici, $m=3$.
Et combien y a-t-il de morceaux différents de taille $m$ dans un texte de taille $n$ ? $n-m+1$.
Cela fait donc en tout $m\times(n-m+1)=nm-m^2+m$ comparaisons, soit 24 ici.
Traçons l’évolution du temps d’exécution de cherche_mot en fonction de la taille du texte pour une taille du mot fixe.
from time import time
from random import randint
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (15, 5)
I, T_in, T_ch = [], [], []
mot = '&'*100
for i in range(10000,500000,10000):
texte = rockyou[:i]
start = time()
cherche_mot(mot,texte)
stop = time()
T_ch.append(stop-start)
I.append(i)
plt.figure(figsize = (15,5))
plt.plot(I,T_ch)
plt.xlabel("longeur du texte (longueur mot = moitié longueur texte)")
plt.ylabel("temps d'exécution (s)")
plt.title("Temps d'excution de 'cherche_mot' en fonction de la taille du texte")
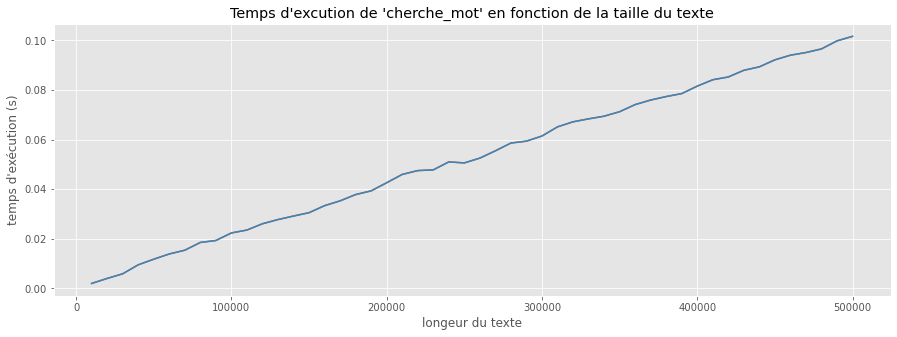
Sur le même modèle, vous allez tracer l’évolution du temps d’exécution de cherche_mot en fonction de la taille du mot pour une taille de texte fixe et pour des mots petits devant le texte.
Pour cela vous compléterez le code ci-dessous.
I, T_ch_mot = [], []
texte = rockyou[:200000]
for i in range(1000,20000,1000):
# à compléter (i doit correspondre au nombre de caractères du mot)
fig,ax = plt.subplots(figsize = (15,5))
ax.plot(I,T_ch_mot)
ax.set(xlabel="longueur du mot", ylabel="temps d'exécution (s)")
ax.set_title("Temps d'excution de 'cherche_mot' en fonction de la longueur du mot")
Code complété (cliquer pour afficher)
I, T_ch_mot = [], [] texte = rockyou[:250000] for i in range(1000,12500,500): mot = 'f'*i # mot de i lettres start = time() cherche_mot(mot,texte) stop = time() T_ch_mot.append(stop-start) I.append(i) fig,ax = plt.subplots(figsize = (15,5)) ax.plot(I,T_ch_mot) ax.set(xlabel="longueur du mot", ylabel="temps d'exécution (s)") ax.set_title("Temps d'excution de 'cherche_mot' en fonction de la longueur du mot")
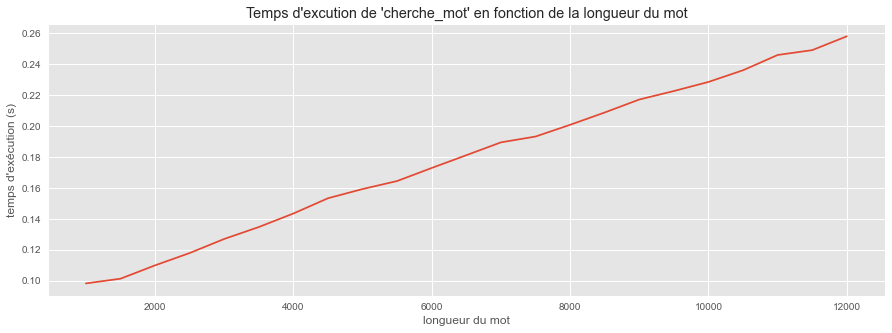
Pour des petits mots par rapport au texte et en appelant $n$ la longueur du texte et $m$ la longueur du mot, quelle fonction semble-t-elle le mieux modéliser l’évolution du temps d’exécution en fonction de $n$ et $m$ ?
- A : $a\times m + b\times n$ où $a$ et $b$ sont des constantes
- B : $a\times m^2$ où $a$ est une constante
- C : $a\times n^2$ où $a$ est une constante
- D : $a\times m\times n$ où $a$ est une constante
Correction (cliquer pour afficher)
Le premier graphique nous montre que pour une taille de mot $m$ fixée, le temps d'exécution semble proportionnel à la taille $n$ du texte.
Le deuxième graphique nous montre que pour une taille de texte $n$ fixée, le temps d'exécution semble proportionnel à la taille $m$ du mot.
On peut donc supposé un temps d'exécution proportionnel à $n\times m$ (réponse D).
Chercher un doublon
La fonction suivante cherche si un élément d’une liste se trouve en double et le cas échéant, le retourne.
def cherche_duplicata(liste):
N = len(liste)
for i in range(N):
for j in range(N):
if i != j and liste[i] == liste[j]:
print('Un élément en double a été trouvé :')
return liste[i]
return 'Pas de doublons trouvés 😞'
liste_fruits = ["🍓", "🍐", "🍊", "🍌", "🍍", "🍑", "🍎", "🍈", "🍊", "🍇"]
a = cherche_duplicata(liste_fruits)
print(a)
Un élément en double a été trouvé :
🍊
Combien de fois la comparaison
liste[i] == liste[j]est-elle opérée au maximum si la liste contient 200 éléments ?
Correction (cliquer pour afficher)
Pour chacun des $N$ tours dans la boucle principale, on réalise $N-1$ fois la comparaison (on compare à tous les éléments sauf lui-même). Cela fait $N\times(N-1)=N^2-N$.
Soit ici, $39\,800$ comparaisons.
On peut aisément améliorer la fonction en évitant de doubler les comparaisons :
def cherche_duplicata_bis(liste):
N = len(liste)
for i in range(N-1):
for j in range(i+1,N):
if liste[i] == liste[j]:
print('Un élément en double a été trouvé :')
return liste[i]
return 'Pas de doublons trouvés 😞'
liste_fruits = ["🍓", "🍐", "🍊", "🍌", "🍍", "🍑", "🍎", "🍈", "🍊", "🍇"]
a = cherche_duplicata(liste_fruits)
print(a)
Un élément en double a été trouvé :
🍊
Combien de comparaisons sont opérées au maximum avec cette nouvelle fonction si la liste contient 200 éléments ?
# Pour vous aider à raisonner
N = 10
for i in range(N-1) :
L = []
for j in range(i+1,N) :
L.append((i,j))
print(L)
[(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (0, 9)]
[(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (1, 9)]
[(2, 3), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (2, 9)]
[(3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (3, 9)]
[(4, 5), (4, 6), (4, 7), (4, 8), (4, 9)]
[(5, 6), (5, 7), (5, 8), (5, 9)]
[(6, 7), (6, 8), (6, 9)]
[(7, 8), (7, 9)]
[(8, 9)]
Correction (cliquer pour afficher)
Il y a $N-1$ comparaisons dans la première itération de la boucle principale, $N-2$ dans la deuxième, $N-3$ dans la troisième, etc.
Et il y aura $N-1$ tours dans la boucle principale.
Cela donne : $\sum_{i=1}^{N-1} (N-i)$ $= N(N-1) - (N-1)(1+N-1)/2$ $=N(N-1)/2$ $=N^2/2 - N/2$.
Et donc ici : $19\,900$ comparaisons
from random import randint
I, T_dup, T_dup_bis = [], [], []
for i in range(200,5000,200) :
L = [i for i in range(i)]
start = time()
cherche_duplicata(L)
stop1 = time()
cherche_duplicata_bis(L)
stop2 = time()
I.append(i)
T_dup.append(stop1-start)
T_dup_bis.append(stop2-stop1)
fig,axs = plt.subplots(3,figsize = (15,15))
axs[0].plot(I,T_dup)
axs[0].set_title("cherche_duplicata")
axs[1].plot(I,T_dup_bis,c='#3388BB',label="cherche_duplicata_bis")
axs[1].set_title("cherche_duplicata_bis")
axs[2].plot(I,T_dup,label="cherche_duplicata")
axs[2].plot(I,T_dup_bis,c='#3388BB',label="cherche_duplicata_bis")
axs[2].set_title("Comparaison")
axs[2].legend()
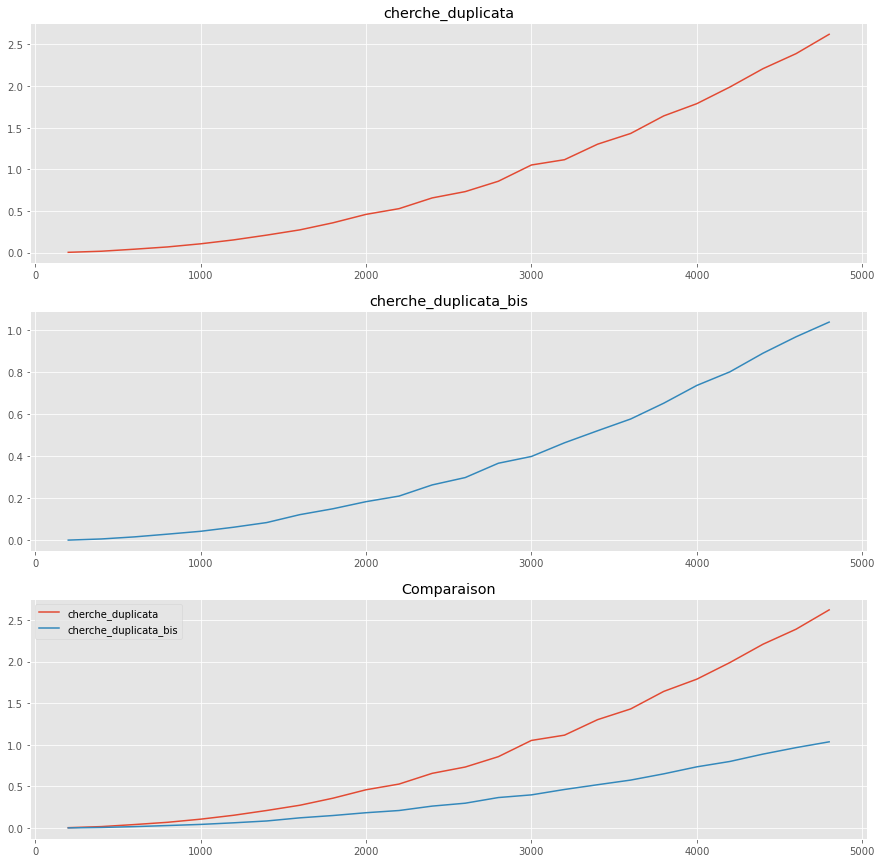
On constate que même si l’amélioration est visible entre les deux fonctions, le comportement général (la classe de complexité comme on le verra plus tard) est identique.
Commentaire (cliquer pour afficher)
Ici, on peut résumer la complexité au comptage des comparaisons.
Le premier algorithme opère $N(N-1)$ comparaisons et le deuxième $N(N-1)/2$.
On a bien divisé le nombre de comparaisons par deux mais la complexité est quadratique dans les deux cas (en $O(n^2)$ car le terme qui domine la croissance de la fonction donnant le nombre de comparaisons est dans les deux cas en $N^2$).
Cela traduit le fait que dans les deux cas, pour des grandes listes, si la taille de la liste est multipliée par $a$, alors le nombre de comparaisons est approximativement multiplié par $a^2$ !
Intégration numérique
def trapeze(f, a, b):
return (f(a) + f(b))/2 * (b - a)
def rect_gauche(f, a, b):
return f(a)*(b-a)
def integrale(f, a, b, n, methode):
p = (b-a)/n
s = 0
for i in range(n) :
s += methode(f,a+i*p,a+(i+1)*p)
return s
def f(x) :
return np.cos(x)*x**2 + 10
Commentaire (cliquer pour afficher)
Le code ci-dessus est dit modulaire dans le sens où plutôt qu'utiliser un gros bloc de code, l'algorithme est découpée en différentes fonctions.
Deux gros avantages à ce type d'écriture :
- la lecture et la compréhension du code sont facilitées ;
- le code est beaucoup plus facilement adaptable (facile d'ajouter ou changer la méthode d'intégration utilisée ou de modifier la fonction intégrée).
import numpy as np
import matplotlib.patches as patches
a = -np.pi
b = 3/2*np.pi
x = np.linspace(a,b,2000)
y = f(x)
n_possibles = (6,10,20,50,200)
fig,axs = plt.subplots(5,2,figsize=(20,20))
for k in range(5) :
n = n_possibles[k]
p = (b-a)/n
I_rect = integrale(f,a,b,n,rect_gauche)
I_trap = integrale(f,a,b,n,trapeze)
for i in range(n) :
rect = plt.Polygon(((a+i*p,0),(a+i*p,f(a+i*p)),(a+(i+1)*p,f(a+i*p)),(a+(i+1)*p,0),(a+i*p,0)),alpha=0.5,facecolor='#9988DD',edgecolor='#9988DD')
trap = plt.Polygon(((a+i*p,0),(a+i*p,f(a+i*p)),(a+(i+1)*p,f(a+(i+1)*p)),(a+(i+1)*p,0),(a+i*p,0)),alpha=0.5,edgecolor='#3388BB')
for j in range(2) :
axs[k][j].plot(x,y,c='#EE6666')
axs[k][0].add_patch(rect)
axs[k][1].add_patch(trap)
axs[k][0].text(0,4,s=f'I = {I_rect:.2f}',fontsize=18,c='w',horizontalalignment='center')
axs[k][1].text(0,4,s=f'I = {I_trap:.2f}',fontsize=18,c='w',horizontalalignment='center')
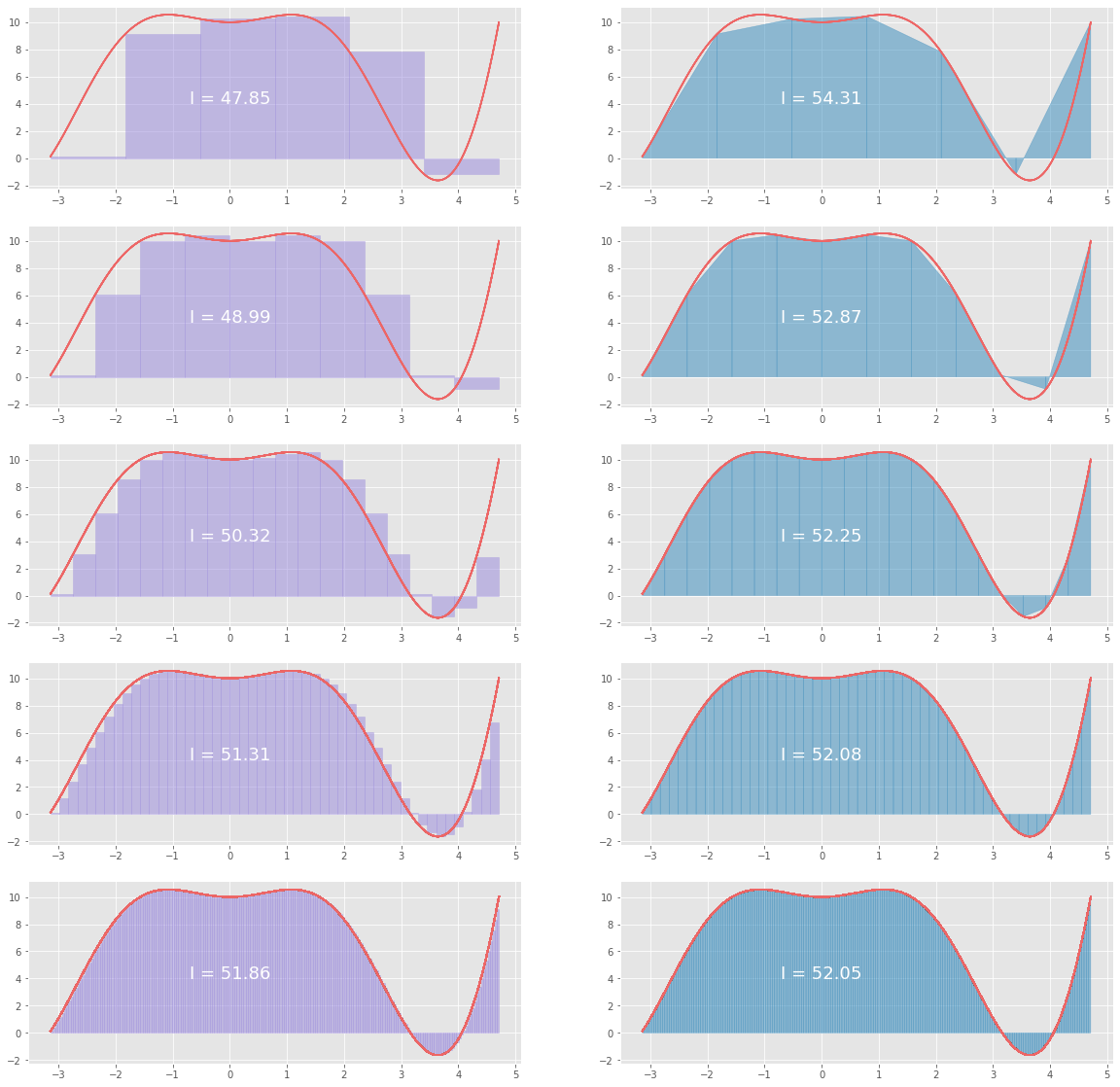
À comparer à : $$ \int_{-\pi}^{3\pi/2}(x^2\cos(x)+10)dx = 2+23\pi-9\frac{\pi^2}{4}\approx 52,05$$
Pour quelle valeur de $n$, la valeur de $I$ atteint-elle 52,0 (à 0,5 près) avec la méthode des rectangles à gauche ?
Vous appelerez cette valeurn_cibleet votre code devra l’afficher.
Correction (cliquer pour afficher)
Savoir tester une convergence, ou comme ici, trouver au bout de combien d'étapes un algorithme a convergé vers une valeur cible pour une imprécision donnée, est très important.
Cela se fait le plus fréquemment avec une bouclewhile.Cela donne $70$ étapes pour la méthode des rectangles à gauche alors qu'on voit sur le graphique qu'il n'a fallu qu'entre 10 et 20 étapes pour la méthode des trapèzes (remplacerI = 0 n_cible = 1 while not(52+0.5 >= I >= 52-0.5): # 52,0 ± 0,5 I = integrale(f, a, b, n_cible, rect_gauche) n_cible += 1 print(n_cible)rect_gauchepartrapezedans le code ci-dessus donne bien d'ailleurs $15$)