L’idée de ce TP est de constater combien des modules/bibliothèques adaptés peuvent fournir des outils puissants et permettre un gain de temps gigantesque.
On va se placer dans un des champs les plus porteurs actuellement (et où python est très utilisé), l’analyse de données.
Cliquez sur cette invitation pour récupérer le repository du TP.
Exploration d’un jeu de données
Statistiques simples
import pandas as pd # bibliothèques dédiée au traitement de jeux de données
import matplotlib.pyplot as plt # bibliothèque graphique
import seaborn as sns # bibliothèque graphique reposant sur matplotlib et dédiée plus particulièrement à la représentation de jeux de données
import numpy as np # bibliothèque puissante permettant de gérer des tableaux multidimensionnels
import plotly.express as px # libraire permettant des graphes interactifs
import plotly.graph_objects as go # complémentaire à la première (seulement utile dans les cas complexes)
Pour pouvoir être importé, un module doit avoir été préalablement installé. Les plus importants sont installés par défaut dans certaines distributions (comme Anaconda).
Les gros modules sont généralement importés sous la forme import module as x où x est un raccourci pour le nom du module (np pour numpy ou plt pour matplotlib.pyplot). Se référer au cours Python pour les autres formes d’importation.
Pour obtenir de l’aide sur un module, on peut demander à Python (help(pd) par exemple pour avoir de l’aide sur pandas ou help(pd.read_csv) pour avoir de l’aide sur la fonction spécifique read_csv), mais il y a généralement beaucoup moins indigeste : l’aide en ligne des modules (pour Pandas par exemple).
# paramètres par défaut pour les graphes
plt.rcParams['figure.figsize'] = (15, 6)
plt.rcParams['font.family'] = "serif"
plt.rcParams['font.size'] = 13
sns.set_style("white")
Le premier jeu de données qu’on va utiliser est issu du World Happiness report (une publication annuelle de l’ONU mesurant le degrés de bonheur de la population mondiale par pays à partir de sondages).
url = "https://raw.githubusercontent.com/Info-TSI-Vieljeux/s1-tp3/main/2020.csv"
data_monde = pd.read_csv(url,sep=";",index_col=0) # data_monde est une dataframe Pandas
# Une dataframe est une sorte de dictionnaire dont les clés sont les en-têtes des colonnes et dont les lignes sont indexées.
data_monde
| Région du monde | Score de bonheur | Écart-type | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | Score de bonheur en Distopie | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pays | ||||||||||
| Finland | Western Europe | 7.8087 | 0.031156 | 10.639267 | 0.954330 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | 1.972317 |
| Denmark | Western Europe | 7.6456 | 0.033492 | 10.774001 | 0.955991 | 72.402504 | 0.951444 | 0.066202 | 0.168489 | 1.972317 |
| Switzerland | Western Europe | 7.5599 | 0.035014 | 10.979933 | 0.942847 | 74.102448 | 0.921337 | 0.105911 | 0.303728 | 1.972317 |
| Iceland | Western Europe | 7.5045 | 0.059616 | 10.772559 | 0.974670 | 73.000000 | 0.948892 | 0.246944 | 0.711710 | 1.972317 |
| Norway | Western Europe | 7.4880 | 0.034837 | 11.087804 | 0.952487 | 73.200783 | 0.955750 | 0.134533 | 0.263218 | 1.972317 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| Central African Republic | Sub-Saharan Africa | 3.4759 | 0.115183 | 6.625160 | 0.319460 | 45.200001 | 0.640881 | 0.082410 | 0.891807 | 1.972317 |
| Rwanda | Sub-Saharan Africa | 3.3123 | 0.052425 | 7.600104 | 0.540835 | 61.098846 | 0.900589 | 0.055484 | 0.183541 | 1.972317 |
| Zimbabwe | Sub-Saharan Africa | 3.2992 | 0.058674 | 7.865712 | 0.763093 | 55.617260 | 0.711458 | -0.072064 | 0.810237 | 1.972317 |
| South Sudan | Sub-Saharan Africa | 2.8166 | 0.107610 | 7.425360 | 0.553707 | 51.000000 | 0.451314 | 0.016519 | 0.763417 | 1.972317 |
| Afghanistan | South Asia | 2.5669 | 0.031311 | 7.462861 | 0.470367 | 52.590000 | 0.396573 | -0.096429 | 0.933687 | 1.972317 |
153 rows × 10 columns
Précisions sur ces données :
- le score de bonheur est un score sur 10 correspondant à la moyenne des réponses des sondés (0 correspond à la pire vie possible et 10 à la meilleure)
- ce n’est pas le PIB par habitant mais son logarithme qui est utilisé pour ne pas avoir des valeurs sur des ordres de grandeur trop différents d’une colonne à l’autre
- entraide sociale : moyenne des réponses à la question binaire “en cas de difficultés, pouvez-vous compter sur de la famille ou des amis pour vous aider ?” (0 : non, 1 : oui)
- liberté des choix de vie : moyenne des réponses à la question binaire “êtes-vous satisfait ou non de votre liberté à choisir ce que vous voulez faire de votre vie ?” (0 : non, 1 : oui)
- générosité : moyenne des réponses à “Avez-vous donné à une association caritative le mois dernier ?” ajustée par rapport au PIB par habitant (valeur résiduelle)
- corruption perçue : moyenne des réponses à la question binaire “la corruption est-elle répandue dans le gouvernement ?” (0 : non, 1 : oui)
On simplifie un peu le jeu de données en retirant la colonne ‘Écart-type’ et ‘Score de bonheur en distopie’ (score minimal obtenu).
data_monde.drop(columns=['Écart-type','Score de bonheur en Distopie'], inplace=True)
data_monde.head(3)
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | |
|---|---|---|---|---|---|---|---|---|
| Pays | ||||||||
| Finland | Western Europe | 7.8087 | 10.639267 | 0.954330 | 71.900825 | 0.949172 | -0.059482 | 0.195445 |
| Denmark | Western Europe | 7.6456 | 10.774001 | 0.955991 | 72.402504 | 0.951444 | 0.066202 | 0.168489 |
| Switzerland | Western Europe | 7.5599 | 10.979933 | 0.942847 | 74.102448 | 0.921337 | 0.105911 | 0.303728 |
data_monde.tail(3)
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | |
|---|---|---|---|---|---|---|---|---|
| Pays | ||||||||
| Zimbabwe | Sub-Saharan Africa | 3.2992 | 7.865712 | 0.763093 | 55.61726 | 0.711458 | -0.072064 | 0.810237 |
| South Sudan | Sub-Saharan Africa | 2.8166 | 7.425360 | 0.553707 | 51.00000 | 0.451314 | 0.016519 | 0.763417 |
| Afghanistan | South Asia | 2.5669 | 7.462861 | 0.470367 | 52.59000 | 0.396573 | -0.096429 | 0.933687 |
Traçons un histogramme brut du jeu de données complet pour y voir plus clair (la librairie Seaborn rend cela très simple).
sns.histplot(data=data_monde)
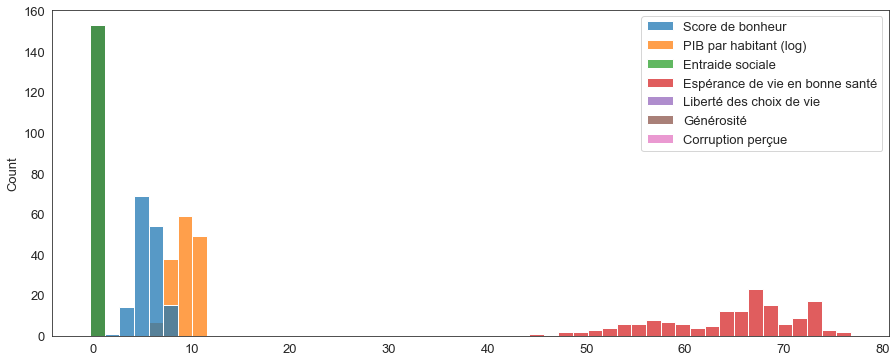
La méthode describe s’appliquant à des dataframe pandas retourne un résumé statistique très pratique des données de chaque colonne :
data_monde.describe()
| Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | |
|---|---|---|---|---|---|---|---|
| count | 153.00000 | 153.000000 | 153.000000 | 153.000000 | 153.000000 | 153.000000 | 153.000000 |
| mean | 5.47324 | 9.295706 | 0.808721 | 64.445529 | 0.783360 | -0.014568 | 0.733120 |
| std | 1.11227 | 1.201588 | 0.121453 | 7.057848 | 0.117786 | 0.151809 | 0.175172 |
| min | 2.56690 | 6.492642 | 0.319460 | 45.200001 | 0.396573 | -0.300907 | 0.109784 |
| 25% | 4.72410 | 8.350645 | 0.737217 | 58.961712 | 0.714839 | -0.127015 | 0.683019 |
| 50% | 5.51500 | 9.456313 | 0.829204 | 66.305145 | 0.799805 | -0.033665 | 0.783122 |
| 75% | 6.22850 | 10.265124 | 0.906747 | 69.289192 | 0.877709 | 0.085429 | 0.849151 |
| max | 7.80870 | 11.450681 | 0.974670 | 76.804581 | 0.974998 | 0.560664 | 0.935585 |
Pour confirmer certaines des valeurs, vous allez construire différentes fonctions :
- une fonction
decomptequi retourne le nombre d’éléments d’une liste,- une fonction
moyennequi retourne la moyenne des éléments d’une liste,- une fonction
medianequi retourne la médiane des éléments d’une liste triée en ordre croissant.L’utilisation de fonctions statistiques déjà existantes est bien sûr prohibée.
def decompte(L):
"""
decompte(L: liste) -> entier
"""
# CODE
def moyenne(L):
"""
decompte(L: liste) -> flottant
"""
# CODE
def mediane(L):
"""
decompte(L: liste) -> floattant ou entier (suivant les valeurs de L)
"""
# CODE
Correction (cliquer pour afficher)
def decompte(L): return len(L)def moyenne(L): s = 0 for e in L: s += e return s/len(L)def mediane(L): N = decompte(L) return L[N//2]
Calculez, pour les 3 formes d’importation du module, l’écart-type des éléments de la liste
Liste_scoresen utilisant la fonctionstdevdu modulestatistics.
Il s’agit d’évaluer directement l’expresion (le nombre doit s’afficher sous la cellule sans utiliser de
import statistics
# CODE
from statistics import *
# CODE
import statistics as st
# CODE
Correction (cliquer pour afficher)
import statistics statistics.stdev(Liste_scores)from statistics import * # Rq : on évite le plus souvent ce type d'importation qui peut générer des conflits de définition. stdev(Liste_scores)import statistics as st # C'est la forme la plus pratique si le module est souvent utilisé st.stdev(Liste_scores)
Traçons maintenant un diagramme en bâtons des scores de bonheur des 60 premiers pays.
fig,ax = plt.subplots(figsize=(20,4))
sns.barplot(ax = ax,x = data_monde.index[:60], y = data_monde['Score de bonheur'].head(60))
plt.xticks(rotation=90)
ax.set_xlabel('')
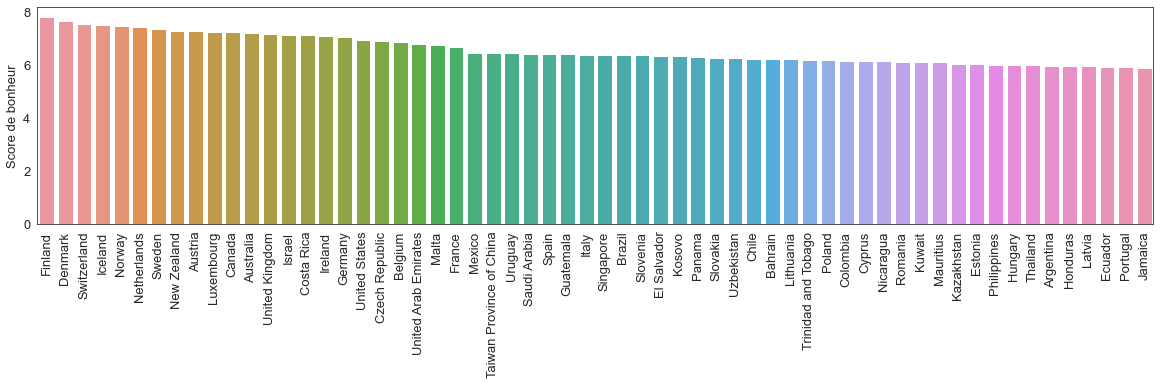
On remarque que les pays sont classés par score de bonheur décroissant dans le jeu de données d’origine.
Mais on peut évidemment choisir un autre critère de classement si on le désire :
data_monde.sort_values(by="PIB par habitant (log)",ascending=True).head(10)
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | |
|---|---|---|---|---|---|---|---|---|
| Pays | ||||||||
| Burundi | Sub-Saharan Africa | 3.7753 | 6.492642 | 0.490326 | 53.400002 | 0.626350 | -0.017552 | 0.606935 |
| Central African Republic | Sub-Saharan Africa | 3.4759 | 6.625160 | 0.319460 | 45.200001 | 0.640881 | 0.082410 | 0.891807 |
| Congo (Kinshasa) | Sub-Saharan Africa | 4.3110 | 6.694256 | 0.672159 | 52.900002 | 0.700794 | 0.083638 | 0.809404 |
| Niger | Sub-Saharan Africa | 4.9096 | 6.842167 | 0.617435 | 53.500095 | 0.759772 | 0.013861 | 0.722530 |
| Liberia | Sub-Saharan Africa | 4.5579 | 7.054380 | 0.709281 | 56.096313 | 0.735269 | 0.042273 | 0.856376 |
| Malawi | Sub-Saharan Africa | 3.5380 | 7.062226 | 0.544007 | 57.592888 | 0.803223 | 0.021433 | 0.731701 |
| Mozambique | Sub-Saharan Africa | 4.6236 | 7.069346 | 0.723874 | 54.205822 | 0.864452 | 0.032376 | 0.683019 |
| Sierra Leone | Sub-Saharan Africa | 3.9264 | 7.268803 | 0.636142 | 50.865143 | 0.715315 | 0.088661 | 0.861331 |
| Madagascar | Sub-Saharan Africa | 4.1656 | 7.281686 | 0.668196 | 59.105427 | 0.557574 | -0.011824 | 0.817486 |
| Gambia | Sub-Saharan Africa | 4.7506 | 7.321815 | 0.693169 | 55.012016 | 0.733163 | 0.343199 | 0.690718 |
data_monde.sort_values(by="Corruption perçue",ascending=False).head()
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | |
|---|---|---|---|---|---|---|---|---|
| Pays | ||||||||
| Bulgaria | Central and Eastern Europe | 5.1015 | 9.869319 | 0.937840 | 66.803978 | 0.745178 | -0.143908 | 0.935585 |
| Romania | Central and Eastern Europe | 6.1237 | 10.107584 | 0.825162 | 67.207237 | 0.842823 | -0.197815 | 0.934300 |
| Bosnia and Herzegovina | Central and Eastern Europe | 5.6741 | 9.455817 | 0.829204 | 67.808136 | 0.651353 | 0.098275 | 0.933769 |
| Afghanistan | South Asia | 2.5669 | 7.462861 | 0.470367 | 52.590000 | 0.396573 | -0.096429 | 0.933687 |
| Kosovo | Central and Eastern Europe | 6.3252 | 9.204430 | 0.820727 | 63.885555 | 0.861536 | 0.190934 | 0.922328 |
data_monde.sort_values(by="Générosité",ascending=False).iloc[[45]]
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | |
|---|---|---|---|---|---|---|---|---|
| Pays | ||||||||
| Denmark | Western Europe | 7.6456 | 10.774001 | 0.955991 | 72.402504 | 0.951444 | 0.066202 | 0.168489 |
D’après la cellule précédente, le 46e (le 1er est à l’indice 0) meilleur score de générosité appartient au Danemark.
Quel pays correspond à la 59e plus courte espérance de vie en bonne santé ?
Correction (cliquer pour afficher)
On obtient son nom grâce à l'expression suivante :
data_monde.sort_values(by="Espérance de vie en bonne santé",ascending=True).iloc[[58]]
Il s'agit de'Russia'.
On peut aussi aisément filtrer le jeu de données en fonction de n’importe quel critère :
data_monde[(data_monde["Espérance de vie en bonne santé"]>60) & (data_monde["Espérance de vie en bonne santé"]<61)]
# Rq : pandas nécessite les opérateurs logiques bit à bit '&' (et) et '|' (ou)
# plutôt que les opérateurs élément par élément 'and' et 'or' qui lèveraient une erreur.
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | |
|---|---|---|---|---|---|---|---|---|
| Pays | ||||||||
| Kenya | Sub-Saharan Africa | 4.5830 | 8.029776 | 0.702652 | 60.096931 | 0.829748 | 0.294682 | 0.831499 |
| India | South Asia | 3.5733 | 8.849824 | 0.592201 | 60.215187 | 0.881445 | 0.057552 | 0.772043 |
Quel pays possède un score de bonheur inférieur à 5 malgré une valeur de corruption perçue inférieure à 0.5 ?
Correction (cliquer pour afficher)
On obtient son nom grâce à l'expression suivante :
data_monde[(data_monde["Score de bonheur"]<5) & (data_monde["Corruption perçue"]<0.5)]
Il s'agit de'Rwanda'.
Pour récupérer l’ensemble des données d’un pays en particulier, on utilise :
data_monde.loc['France']
Région du monde Western Europe
Score de bonheur 6.6638
PIB par habitant (log) 10.584223
Entraide sociale 0.937104
Espérance de vie en bonne santé 73.801933
Liberté des choix de vie 0.825468
Générosité -0.130642
Corruption perçue 0.583521
Name: France, dtype: object
Pour chaque variable mesurée (chaque colonne), on peut facilement tracer des histogrammes illustrant la répartition des valeurs.
sns.displot(data_monde, x="Score de bonheur", bins=20, kde=True, height=4, aspect=3)
# bins contrôle le nombre de classes
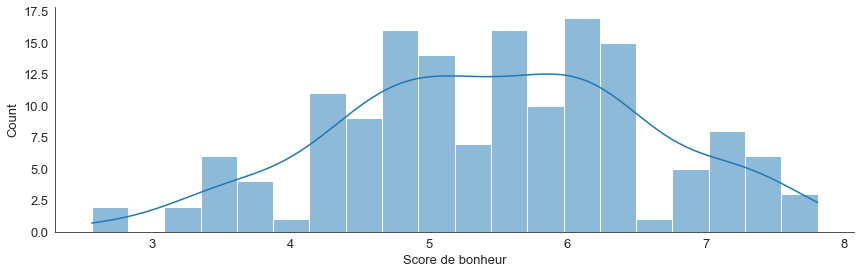
On peut faciliter la lecture des graphes en les rendant interactif.
On utilise pour cela la bibliothèque Plotly express qui sait (comme seaborn) parler à une dataframe pandas.
On peut zoomer sur ces graphiques interactifs et obtenir des informations en survolant avec le curseur.
px.histogram(data_monde,'Corruption perçue',nbins=40,title="Corruption perçue")
# Cette fois-ci, le nombre de classes est désigné par nbins.
Modifiez le graphe précédent pour répondre à cette question : combien la classe la plus peuplée de l’histogramme de l’espérance de vie en bonne santé compte-elle de valeurs si l’histogramme comporte 30 classes ?
Correction (cliquer pour afficher)
On écrit maintenant :
px.histogram(data_monde,'Espérance de vie en bonne santé',nbins=30)
Et on n'a plus qu'à survoler la classe la plus peuplée pour découvrir le nombre de valeurs qu'elle contient : 29.
Regroupement des données
On remarque que le jeu de données contient une colonne catégorielle : “Région du monde”.
Cela va nous permettre d’explorer de possibles dynamiques régionales : est-ce que les pays d’une même zone ont des indicateurs semblables ?
pd.unique(data_monde["Région du monde"]) # permet d'afficher une seule fois chacune des valeurs différentes de la colonne
array(['Western Europe', 'North America and ANZ','Middle East and North Africa', 'Latin America and Caribbean','Central and Eastern Europe', 'East Asia', 'Southeast Asia','Commonwealth of Independent States', 'Sub-Saharan Africa','South Asia'], dtype=object)
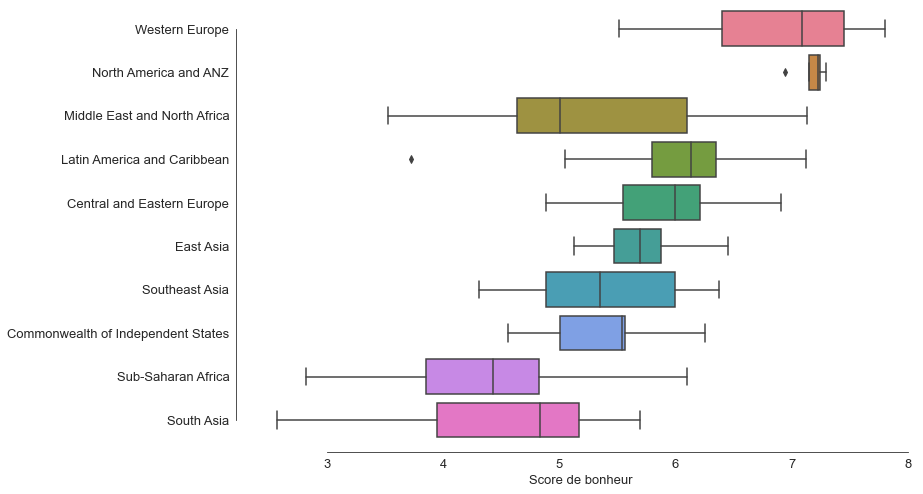
Traçons des diagrammes en boîte à moustaches représentant les scores de bonheur pour chacune des régions.
Construction des boîtes à moustaches (ou diagrammes en boîtes de Tukey) :
Les frontières de la boites sont formées des premier Q1 et troisième quartile Q3 et la barre dans la boite correspond à la médiane (50% des valeurs sont donc dans la boîte).
Pour les moustaches, on calcule d’abord 1,5 fois la distance interquartile entre le premier et le troisième quartile (la longueur de la boîte) : L=1,5×(Q3-Q1). Si les valeurs ne s’étendent pas au-delà de Q1-L et Q3+L, on trace les moustaches aux valeurs min et max. Sinon, on trace les moustaches au niveau des valeurs précédant immédiatement la limite. Les valeurs au-delà sont représentées par des points et sont le plus souvent considérées comme des anomalies.
À nouveau Seaborn rend cela très simple…
sns.set_style("white")
fig, ax = plt.subplots(figsize=(12,8))
sns.boxplot(ax = ax, x="Score de bonheur", y="Région du monde", palette="husl", data=data_monde)
sns.despine(offset=10, trim=True)
ax.set_ylabel('')
Traçons maintenant un graphe plus général représentant toutes les relations possibles entre deux axes du jeu de données pour voir si certaines combinaisons discriminent plus nettement les différentes régions.
# Un peu long à s'exécuter (environ 30 s)
g = sns.pairplot(data_monde, hue="Région du monde", corner=True)
g._legend.set_bbox_to_anchor((0.6, 0.8))
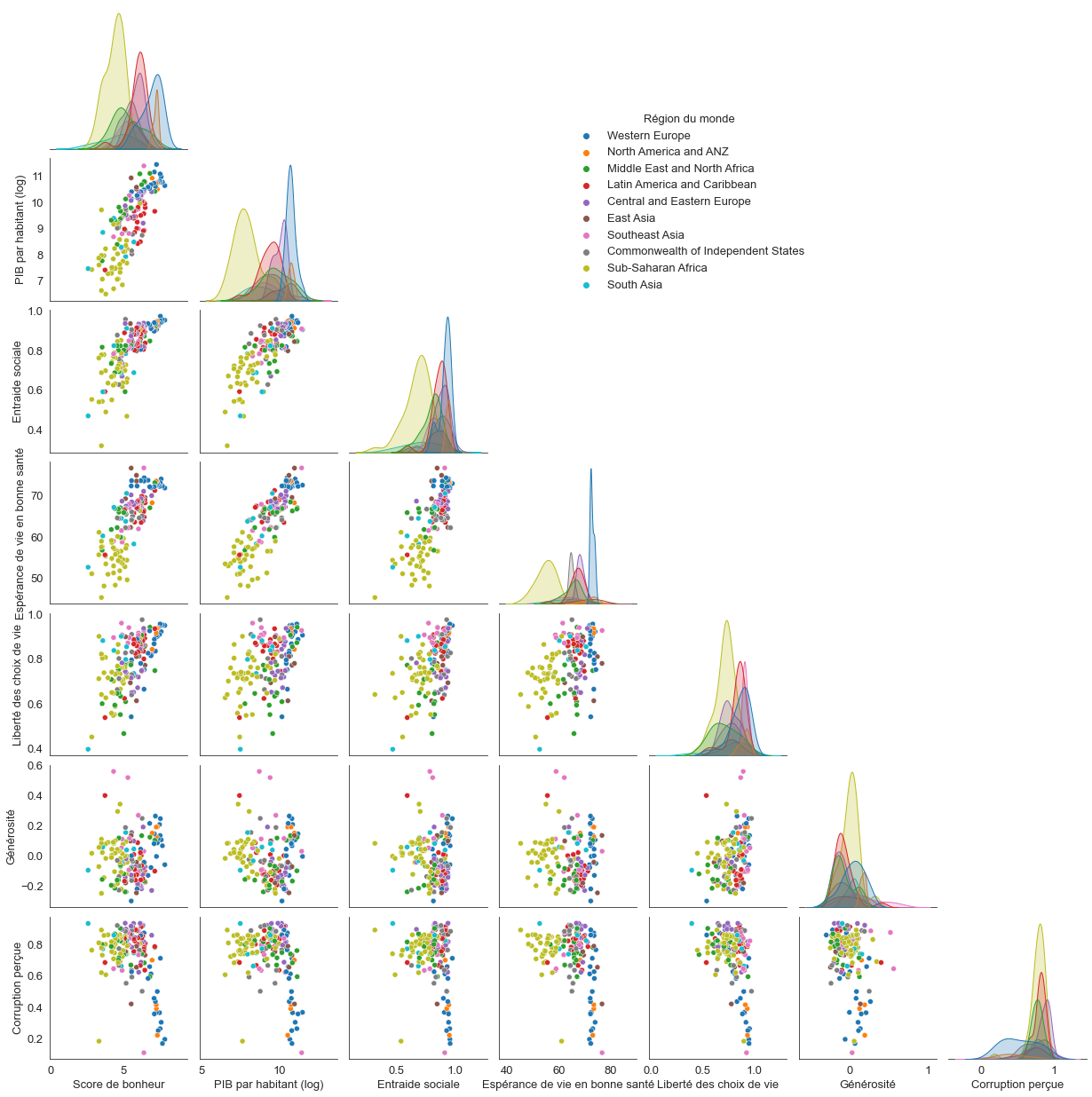
On constate que les groupes régionaux sont relativement homogènes pour la plupart des critères.
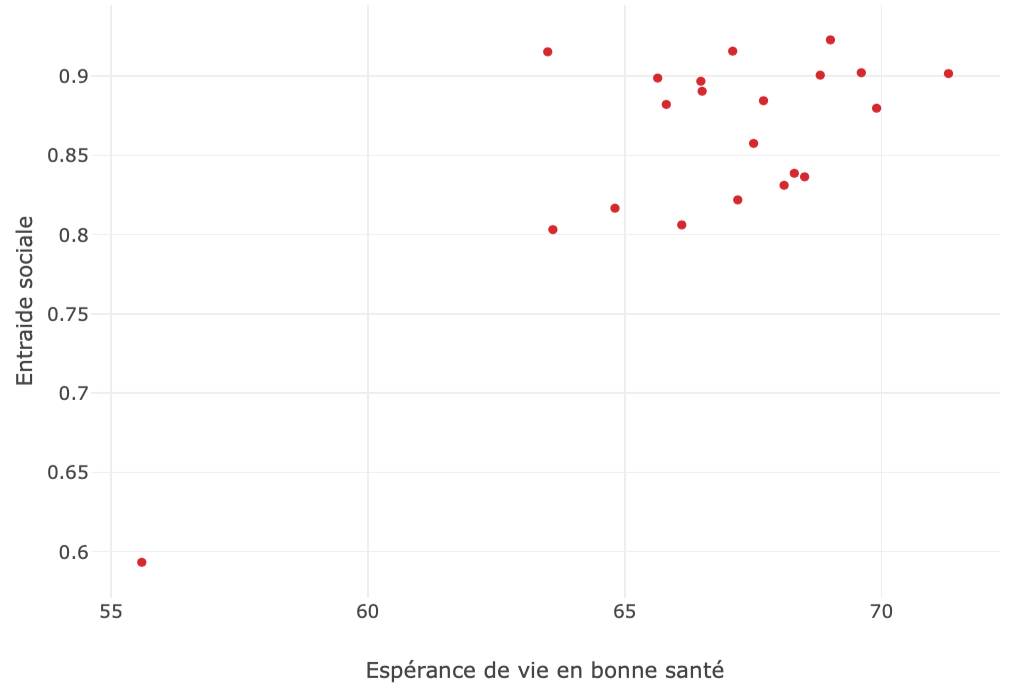
Zoomons sur un de ces graphes :
sns.set_style("whitegrid")
sns.jointplot(data=data_monde,x="PIB par habitant (log)", y="Score de bonheur", hue="Région du monde", kind='scatter', height=8, legend=False)
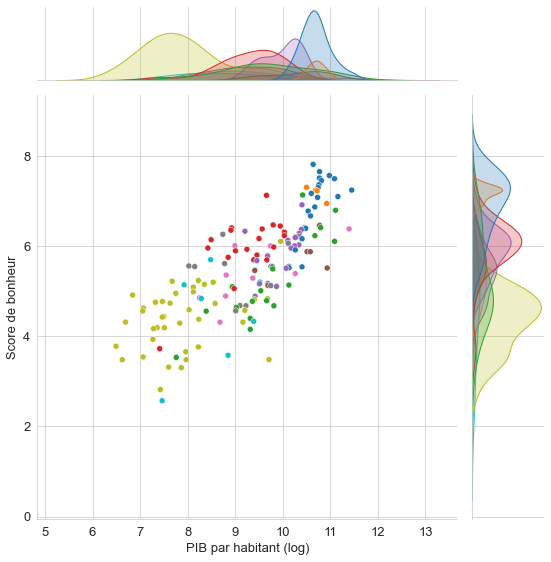
Une version interactive du même graphique permet de consulter les informations pour chaque point :
px.scatter(data_monde,x='PIB par habitant (log)', y='Score de bonheur', hover_name=data_monde.index, color='Région du monde')
Trouvez la région du monde représentée sur le graphe suivant (le graphe interactif permet de trouver la réponse facilement).
Correction (cliquer pour afficher)
Il s'agit de 'Latin America and Caribbean'.
Allons maintenant au-delà de la proximité géographique pour regrouper les pays en 3 grands blocs socioéconomiques : “Nord”, “Sud”, “Intermédiaire”.
conditions = [(data_monde['Région du monde'] == 'Western Europe') | (data_monde['Région du monde'] == 'North America and ANZ'),(data_monde['Région du monde'] == 'South Asia') | (data_monde['Région du monde'] == 'Sub-Saharan Africa')]
choix = ['"Nord"', '"Sud"']
data_monde['Groupe'] = np.select(conditions, choix, default='Autres')
# Un peu long à s'exécuter (environ 30 s)
sns.set_style("white")
g = sns.PairGrid(data_monde, diag_sharey=False, hue="Groupe")
g.map_upper(sns.scatterplot)
g.map_lower(sns.kdeplot,common_norm=False)
g.map_diag(sns.histplot,bins=20,kde=True)
g.add_legend(title="Grands groupes",adjust_subtitles=True)
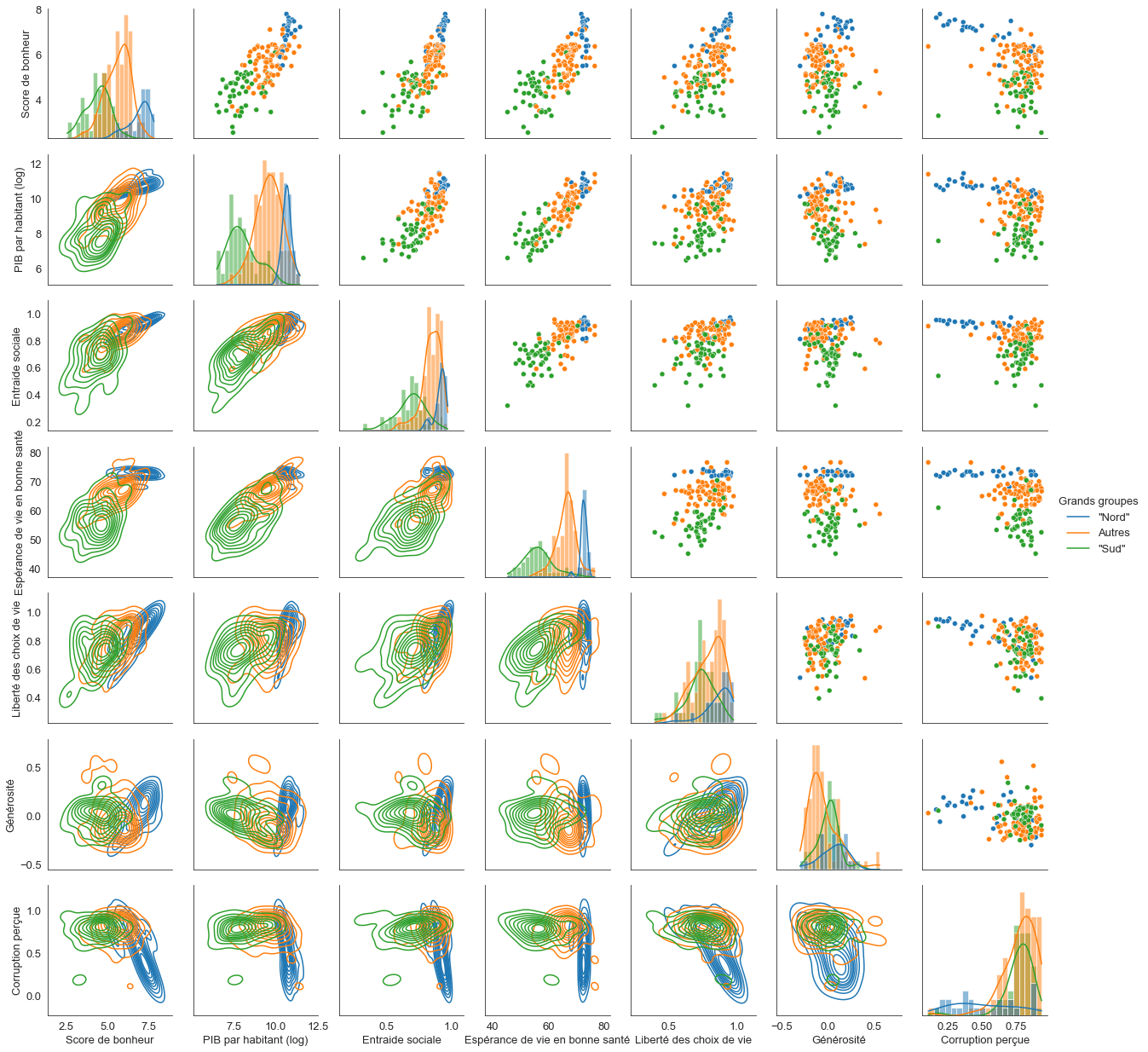
L’homogénéité de ces 3 groupes saute aux yeux.
Corrélations
Les graphiques précédents mettent en évidence des corrélations assez fortes entre certaines grandeurs.
Creusons un peu.
g = sns.PairGrid(data_monde, y_vars=["Score de bonheur"], x_vars=["PIB par habitant (log)", "Corruption perçue"], height=7, aspect=1.5)
g.map(sns.regplot)
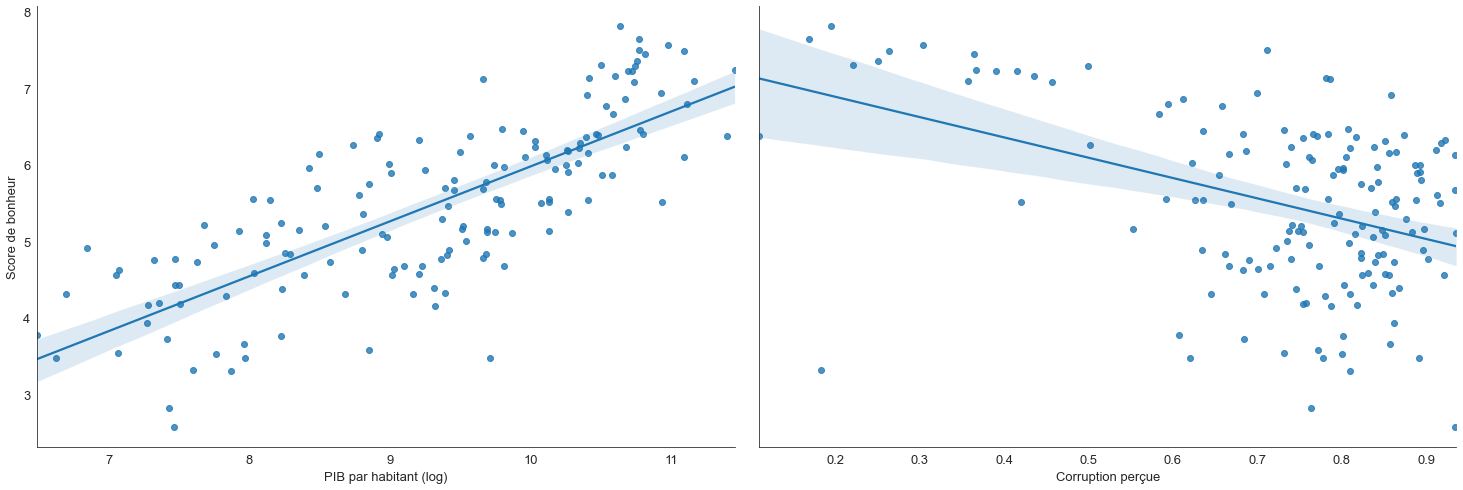
On constate sur cet exemple que le score de bonheur est corrélé positivement avec le PIB par habitant et négativement avec le degré de corruption perçue.
Pour avoir un panorama complet, traçons la matrice de corrélation donnant, pour chaque couple de variable, la valeur du coefficient de corrélation $r$ (valeur entre -1 et 1 traduisant le degré de dépendance linéaire entre deux variables) :
fig, ax = plt.subplots(figsize=(12,10))
cmap = sns.diverging_palette(0, 230, 90, 60, as_cmap=True).reversed() # choix de la palette de couleurs
sns.heatmap(data_monde.iloc[:,1:].corr(), cmap=cmap, center=0, annot=True, fmt=".2f", linewidth = 0.5, ax=ax)
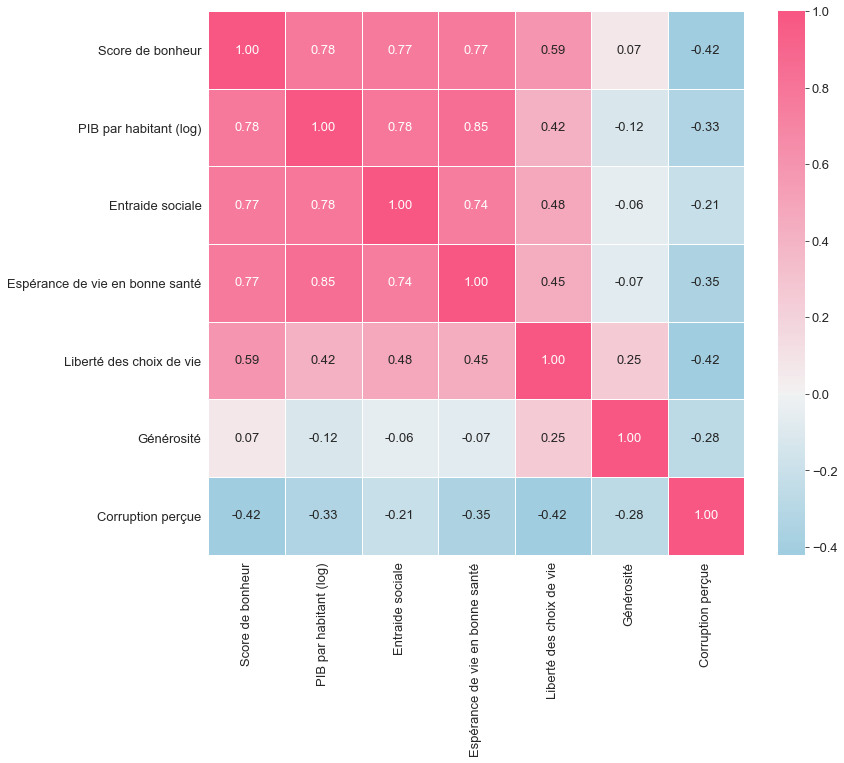
Citez les deux variables les moins corrélées entre elles (donner les noms exacts tels qu’ils apparaissent dans les données, attention à la casse). L’ordre des variables n’est pas important.
Correction (cliquer pour afficher)
Voilà le test utiliser pour vérifier la réponse :assert variable1 == "Générosité" or variable1 == "Entraide sociale" if variable1 == "Générosité": assert variable2 == "Entraide sociale" else: assert variable2 == "Générosité"
Fin du TP3a
Un chouïa d’apprentissage automatique
(machine learning)
On a vu qu’un regroupement des données en 3 grands groupes “Nord”, “Sud” et “Intermédiaire” semble plutôt cohérent.
Mais pourquoi pas laisser un algorithme décider lui-même de qui va le mieux ensemble ? Ensuite nous pourrons vérifier si cela recoupe notre découpage fait à la main.
On appelle cela un apprentissage non supervisé.
Nous allons utiliser l’algorithme des k-moyennes pour partitionner automatiquement nos données.
Il consiste à placer chaque point de données dans un espace à $n$ dimensions où $n$ est le nombre de variables (les descripteurs) et chercher à les regrouper en clusters en fonction de leurs distances.
Chaque variable correspondant à un axe du repère.
Pour aider l’algorithme, on peut tenter de réduire la dimension de l’espace dans lequel chaque point de données est plongé en utilisant une analyse en composantes principales.
L’idée est de déterminer les combinaisons des différentes variables expliquant le mieux la variance des données. Chaque nouvel axe ainsi formé (les composantes principales) explique une part décroissante mais complémentaire de la variance (sur la deuxième composante, les données sont moins étalées que sur la première, mais elles s’étalent dans une direction orthogonale, et ainsi de suite).
Projeter les données sur les premières composantes permet de les étaler le plus possible. On peut ainsi réduire l’espace à n dimensions du départ à un espace de seulement 2 ou 3 dimensions expliquant la majorité de la variance des données.
Commentaire (cliquer pour afficher)
Une vidéo pour ceux qui voudraient en savoir plus sur ce sujet.
L’animation suivante montre comment serait sélectionné l’axe de la composante principale dans un espace à deux dimensions : il correspond à la position de la droite pour laquelle la distance cumulée de tous les points à la droite est la plus grande.
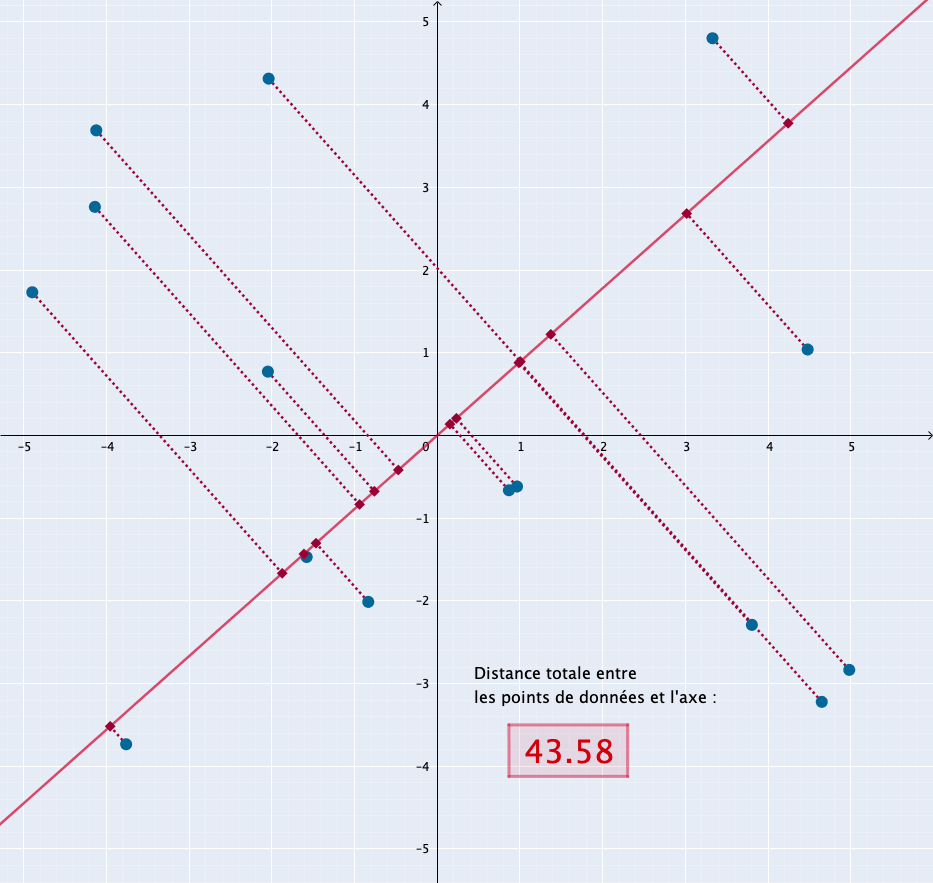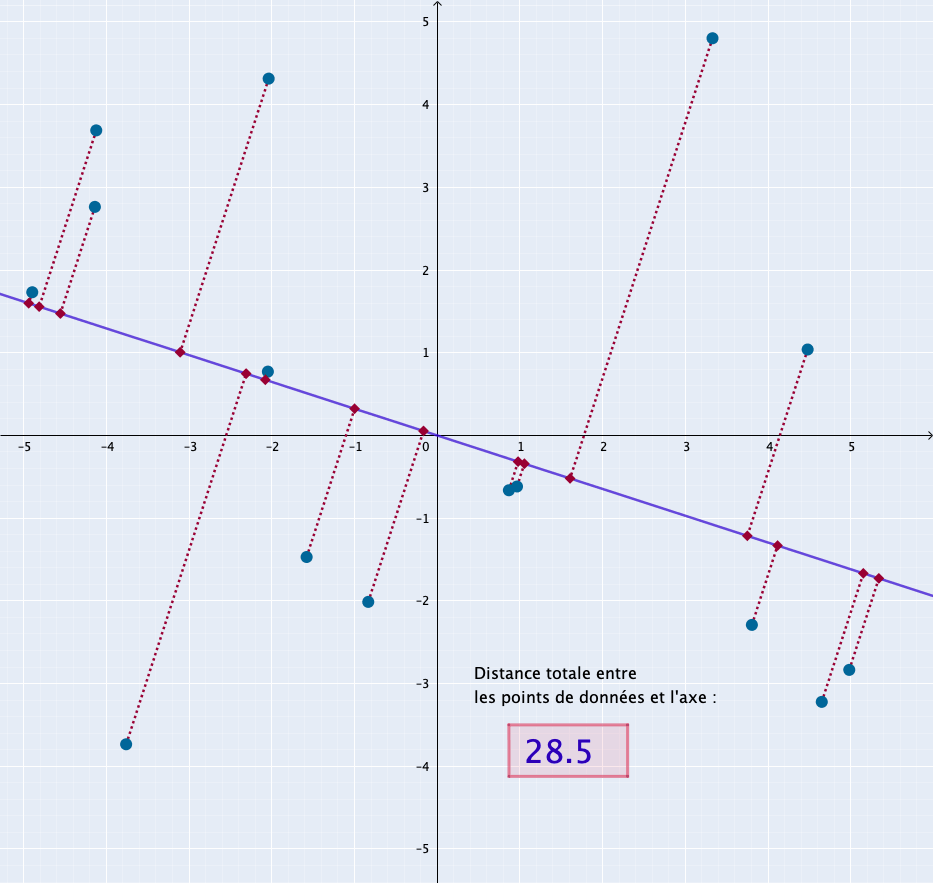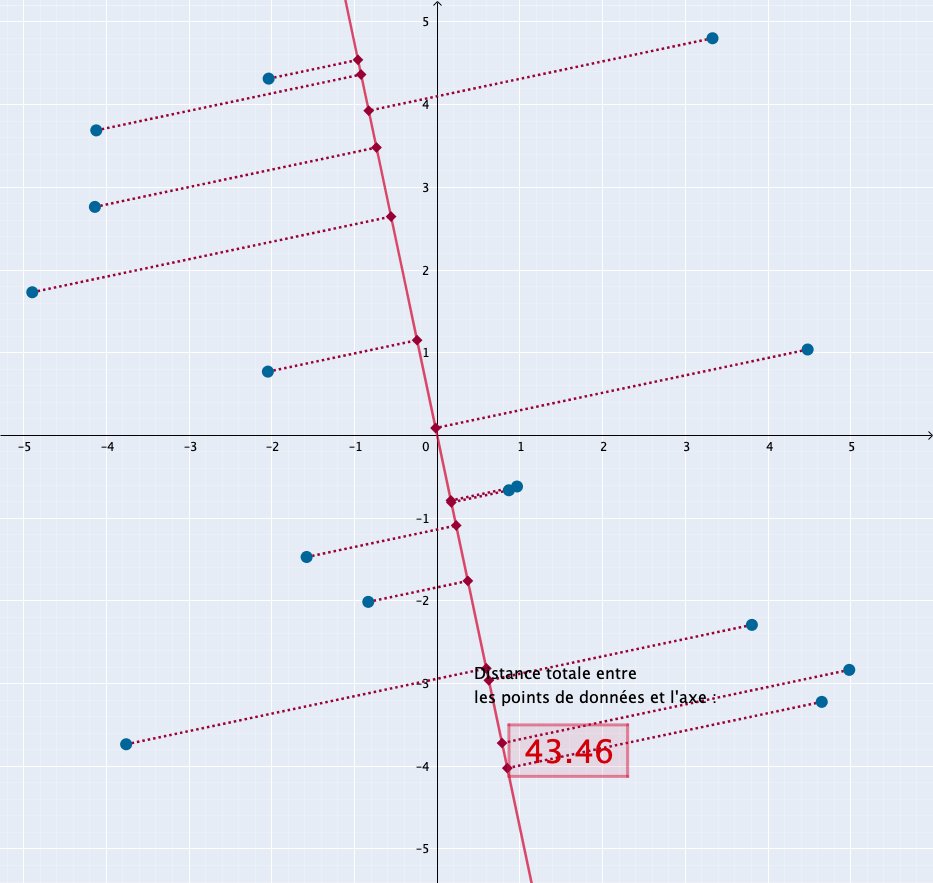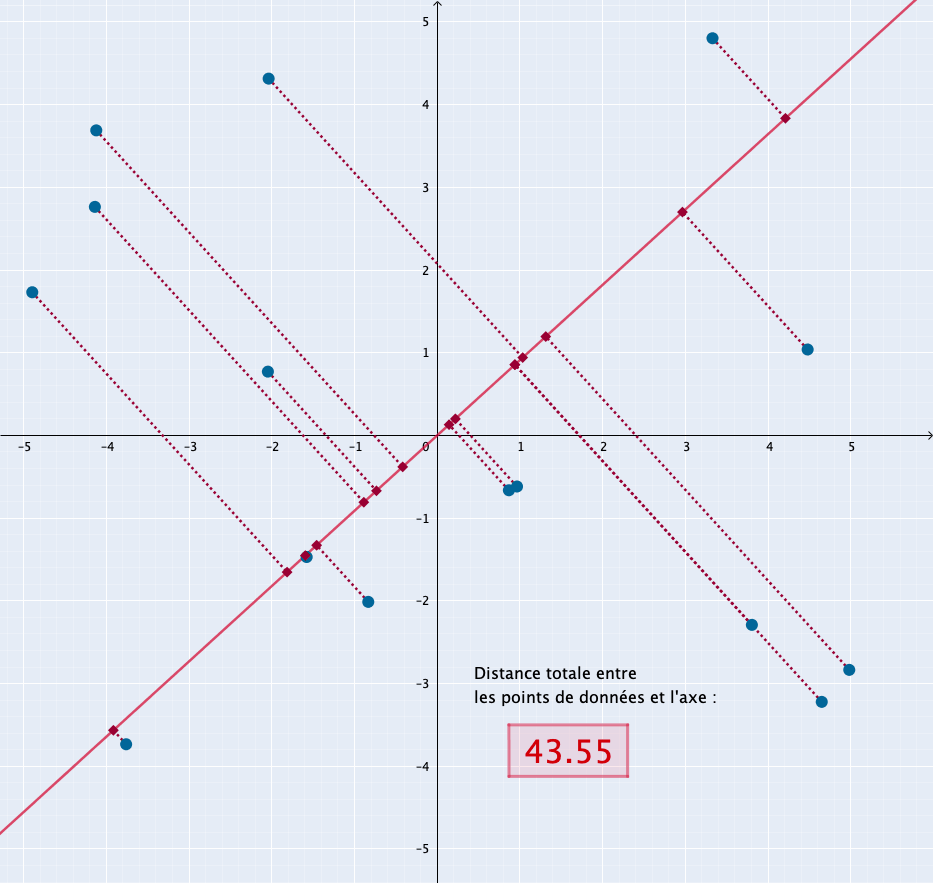
La bibliothèque Scikit-learn, destinée à l’apprentissage automatique, contient tout ce qu’il nous faut :
from sklearn.decomposition import PCA # l'algorithme d'analyse en composantes principales (PCA en anglais)
from sklearn.preprocessing import StandardScaler # pour centrer-réduire les données
from sklearn.cluster import KMeans # l'algorithme des k-moyennes
variables = data_monde.columns.values[1:-1]
scaler = StandardScaler()
X = scaler.fit_transform(data_monde[variables])
# chaque vecteur correspondant à chacune des variables est maintenant centré-réduit
pca = PCA()
components = pca.fit_transform(X)
Quelle combinaison des variables de départ utilise la première composante ? Les quelqus lignes suivantes permettent de le déterminer.
data = data_monde.copy() # pour pouvoir revenir sur le graphe suivant même après ajout de colonnes à data_monde
n_c = 1 # numéro de la composante principale à décrire
px.bar(components.T, x=data.columns.values[1:-1], y=n_c-1, labels={f"{n_c-1}": f"Composante Principale (CP) {n_c}"})
Quelle est le nom de la variable participant le plus à la composante principale n°34 ?
Correction (cliquer pour afficher)
La 'Générosité'.
Représentons le pourcentage de variance expliquée par chacune des composantes :
exp_var_cumul = np.cumsum(pca.explained_variance_ratio_)
fig = px.bar(x=range(1, exp_var_cumul.shape[0] + 1),y=pca.explained_variance_ratio_,labels={"x": "composante", "y": "% variance expliquée"})
fig.add_scatter(x=list(range(1, exp_var_cumul.shape[0] + 1)), y=exp_var_cumul, name="", showlegend=False)
Les trois premières composantes expliquent plus de 80% de la variance !
Plaçons les données dans un espace réduit à ces 3 dimensions :
px.scatter_3d(components, x=0, y=1, z=2,
color=data_monde['Groupe'],
labels={'0': 'CP 1', '1': 'CP 2', '2': 'CP 3'},
hover_name=data_monde.index)
On constate à nouveau que nos 3 groupes discriminent plutôt très bien nos données même si quelques chevauchements existent.
C’est le moment d’utiliser l’algorithme des k-moyennes pour essayer de former 3 groupes homogènes :
# on ne garde que les 3 premières composantes principales
pca = PCA(n_components = 3)
pca.fit(X)
score_pca = pca.transform(X)
kmeans_pca = KMeans(n_clusters=3,init='k-means++',random_state=42)
kmeans_pca.fit(score_pca)
data_monde["Cluster"]=kmeans_pca.labels_.astype(str)
data_monde.head(3)
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | Groupe | Cluster | |
|---|---|---|---|---|---|---|---|---|---|---|
| Pays | ||||||||||
| Finland | Western Europe | 7.8087 | 10.639267 | 0.954330 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | "Nord" | 2 |
| Denmark | Western Europe | 7.6456 | 10.774001 | 0.955991 | 72.402504 | 0.951444 | 0.066202 | 0.168489 | "Nord" | 2 |
| Switzerland | Western Europe | 7.5599 | 10.979933 | 0.942847 | 74.102448 | 0.921337 | 0.105911 | 0.303728 | "Nord" | 2 |
fig = px.scatter_3d(components, x=0, y=1, z=2,
color=data_monde['Cluster'],
labels={'0': 'CP 1', '1': 'CP 2', '2': 'CP 3'},
color_discrete_sequence=px.colors.qualitative.Bold,
hover_name=data_monde.index)
fig.update_layout(legend_title = "Cluster")
Les 3 clusters créés reproduisent à peu de chose près les 3 groupes “Nord”, “Sud”, “Intermédiaire” construits à la main.
À quel cluster correspondent approximativement les pays du groupe “Sud” ?
Correction (cliquer pour afficher)
Au cluster "1".
Mais l’accord n’est pas parfait !
Citez un pays qui appartient au groupe “Nord” mais qui n’appartient pas au cluster lui correspondant.
Correction (cliquer pour afficher)
Un des pays suivant : "Spain", "Italy", "Cyprus", "North Cyprus", "Portugal", "Greece".
On remarque qu'il s'agit exclusivement de pays du sud de l'Europe.
Nous allons voir dans la prochaine partie du TP comment représenter ces données sur une carte pour y voir plus clair.
Fin du TP3b
Un peu de géographie
Le module suivant va permettre d’ajouter à nos données le code à 3 lettres (SO 3166-1 alpha-3) de chaque pays.
Mais pourquoi donc ? plotly express permet de tracer la carte d’un pays directement à partir de ce petit code de 3 lettres !
import country_converter as coco
iso3 = coco.convert(names=data_monde.index, to='ISO3', not_found=None)
data_monde["code"] = iso3
data_monde.head()
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | Groupe | Cluster | code | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pays | |||||||||||
| Finland | Western Europe | 7.8087 | 10.639267 | 0.954330 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | "Nord" | 2 | FIN |
| Denmark | Western Europe | 7.6456 | 10.774001 | 0.955991 | 72.402504 | 0.951444 | 0.066202 | 0.168489 | "Nord" | 2 | DNK |
| Switzerland | Western Europe | 7.5599 | 10.979933 | 0.942847 | 74.102448 | 0.921337 | 0.105911 | 0.303728 | "Nord" | 2 | CHE |
| Iceland | Western Europe | 7.5045 | 10.772559 | 0.974670 | 73.000000 | 0.948892 | 0.246944 | 0.711710 | "Nord" | 2 | ISL |
| Norway | Western Europe | 7.4880 | 11.087804 | 0.952487 | 73.200783 | 0.955750 | 0.134533 | 0.263218 | "Nord" | 2 | NOR |
fig = px.choropleth(data_monde,
locations = "code",
color = "Score de bonheur",
projection = "orthographic",
color_continuous_scale = "Spectral_r",
hover_name = data_monde.index,
hover_data = {"code" : False})
fig.update_geos(
showland = True, landcolor = "LightGrey",
showocean = True, oceancolor = "LightBlue",
showlakes = True, lakecolor = "LightBlue",
showframe = False)
fig.update_layout(margin={"r":0,"t":0,"l":0,"b":0})
fig.show()
On est maintenant paré pour représenter les 3 clusters obtenus par l’algo des k-moyennes du tp3b.
data_monde["Cluster"] = [f'n°{cluster}' for cluster in data_monde["Cluster"].astype('int64') if cluster != 'nan']
data_monde.head(1)
| Région du monde | Score de bonheur | PIB par habitant (log) | Entraide sociale | Espérance de vie en bonne santé | Liberté des choix de vie | Générosité | Corruption perçue | Groupe | Cluster | code | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pays | |||||||||||
| Finland | Western Europe | 7.8087 | 10.639267 | 0.95433 | 71.900825 | 0.949172 | -0.059482 | 0.195445 | "Nord" | n°2 | FIN |
fig = px.choropleth(data_monde,
locations = "code",
color = "Cluster",
projection = "natural earth",
color_discrete_sequence = px.colors.qualitative.Set2,
hover_name = data_monde.index,
hover_data = {"code" : False}
)
#fig.update_geos(fitbounds="locations", visible=True)
fig.update_layout(margin = {"r":0,"t":0,"l":0,"b":0})
fig.update_geos(showframe = False)
fig.show()
Terminons en fabriquant une carte régionale.
for reg in pd.unique(data_monde["Région du monde"]):
print(reg)
Western Europe
North America and ANZ
Middle East and North Africa
Latin America and Caribbean
Central and Eastern Europe
East Asia
Southeast Asia
Commonwealth of Independent States
Sub-Saharan Africa
South Asia
region = data_monde[data_monde["Région du monde"] == "Middle East and North Africa"]
fig = px.choropleth(region,
locations = "code",
color = "Score de bonheur",
projection = "natural earth",
color_continuous_scale = "Temps",
hover_name = region.index,
hover_data = {"code" : False}
)
fig.update_geos(fitbounds = "locations", visible = True)
fig.update_layout(margin = {"r":0,"t":0,"l":0,"b":0})
fig.update_geos(showframe = False, resolution = 50)
fig.show()
Modifiez les cellules qui précèdent pour que le graphique ci-dessus affiche la carte du score de générosité des pays d’Asie du sud-est.
Correction (cliquer pour afficher)
Voilà les lignes modifiées :region = data_monde[data_monde["Région du monde"] == "Southeast Asia"] fig = px.choropleth(region, locations="code", color="Générosité", projection="natural earth", color_continuous_scale="Temps", hover_name = region.index, hover_data ={"code" : False} ) fig.update_geos(fitbounds="locations", visible=True) fig.update_layout(margin={"r":0,"t":0,"l":0,"b":0}) fig.update_geos(showframe = False, resolution=50) fig.show()
De quelle couleur est le Vietnam sur cette carte ?
Correction (cliquer pour afficher)
vert
Fin du TP3c
Série temporelle
Utilisons un nouveau jeu de données comprenant des relevés de consommation électrique allemands entre 2006 et 2018 :
url = "http://cordier-phychi.toile-libre.org/Info/github/elec_allemagne.csv"
serie_temp = pd.read_csv(url,sep=",")
serie_temp.drop(columns="Wind+Solar",inplace=True)
serie_temp
| Date | Consumption | Wind | Solar | |
|---|---|---|---|---|
| 0 | 2006-01-01 | 1069.18400 | NaN | NaN |
| 1 | 2006-01-02 | 1380.52100 | NaN | NaN |
| 2 | 2006-01-03 | 1442.53300 | NaN | NaN |
| 3 | 2006-01-04 | 1457.21700 | NaN | NaN |
| 4 | 2006-01-05 | 1477.13100 | NaN | NaN |
| ... | ... | ... | ... | ... |
| 4378 | 2017-12-27 | 1263.94091 | 394.507 | 16.530 |
| 4379 | 2017-12-28 | 1299.86398 | 506.424 | 14.162 |
| 4380 | 2017-12-29 | 1295.08753 | 584.277 | 29.854 |
| 4381 | 2017-12-30 | 1215.44897 | 721.247 | 7.467 |
| 4382 | 2017-12-31 | 1107.11488 | 721.176 | 19.980 |
4383 rows × 4 columns
Petit toilettage des données : on transforme les valeurs de la colonne des dates en un type date reconnu par pandas et on les utilise comme index.
serie_temp['Date'] = pd.to_datetime(serie_temp['Date'])
serie_temp = serie_temp.set_index('Date')
serie_temp.head()
| Consumption | Wind | Solar | |
|---|---|---|---|
| Date | |||
| 2006-01-01 | 1069.184 | NaN | NaN |
| 2006-01-02 | 1380.521 | NaN | NaN |
| 2006-01-03 | 1442.533 | NaN | NaN |
| 2006-01-04 | 1457.217 | NaN | NaN |
| 2006-01-05 | 1477.131 | NaN | NaN |
On francise ensuite les noms de colonne…
serie_temp.columns = ["Consommation","Vent","Solaire"]
serie_temp.head()
| Consommation | Vent | Solaire | |
|---|---|---|---|
| Date | |||
| 2006-01-01 | 1069.184 | NaN | NaN |
| 2006-01-02 | 1380.521 | NaN | NaN |
| 2006-01-03 | 1442.533 | NaN | NaN |
| 2006-01-04 | 1457.217 | NaN | NaN |
| 2006-01-05 | 1477.131 | NaN | NaN |
Et enfin, on ajoute des colonnes “jour”, “mois” et “année”.
serie_temp['jour'] = serie_temp.index.day_name()
serie_temp['mois'] = serie_temp.index.month
serie_temp['année'] = serie_temp.index.year
serie_temp["date"] = serie_temp.index
serie_temp["date"] = serie_temp["date"].dt.date # pour aider Colab qui a des soucis avec les dates
serie_temp.head()
| Consommation | Vent | Solaire | jour | mois | année | date | |
|---|---|---|---|---|---|---|---|
| Date | |||||||
| 2006-01-01 | 1069.184 | NaN | NaN | Sunday | 1 | 2006 | 2006-01-01 |
| 2006-01-02 | 1380.521 | NaN | NaN | Monday | 1 | 2006 | 2006-01-02 |
| 2006-01-03 | 1442.533 | NaN | NaN | Tuesday | 1 | 2006 | 2006-01-03 |
| 2006-01-04 | 1457.217 | NaN | NaN | Wednesday | 1 | 2006 | 2006-01-04 |
| 2006-01-05 | 1477.131 | NaN | NaN | Thursday | 1 | 2006 | 2006-01-05 |
px.line(serie_temp[["Consommation","Vent","Solaire"]])
On constate d’importantes variations saisonnières.
zoom = serie_temp[serie_temp['année']==2016]
fig1 = px.line(zoom,'date','Consommation')
fig2 = px.scatter(zoom,'date','Consommation',color='jour')
fig = go.Figure()
fig.add_traces([fig1.data[0],*[fig2.data[i] for i in range(7)]])
Une variabilité hebdomadaire se superpose à la tendance saisonnière.
Grâce à la méthode des dataframe pandas groupby, on peut facilement grouper les donner de manière à obtenir les statistiques qui nous intéressent.
Exemple : trouvons combien d’électricité d’origine éolienne a été produite chaque mois en 2016.
serie_temp[serie_temp['année']==2016].groupby("mois")["Vent"].sum()
mois
1 9264.588
2 9814.294
3 6030.177
4 5910.504
5 6089.484
6 3369.069
7 4651.582
8 4742.343
9 4222.315
10 5585.248
11 8076.232
12 9252.290
Name: Vent, dtype: float64
Sur le modèle précédent, déterminez le jour de la semaine où l’Allemagne a consommé le plus d’électricité en moyenne en 2016 (vous pourrez utilisez la méthode
meanà la place desum).
Correction (cliquer pour afficher)
Il suffit d'écrire la ligne suivante :
serie_temp[serie_temp['année']==2016].groupby("jour")["Consommation"].mean()
Et on constate alors que le mercredi est le jour où les allemands ont le plus consommé en moyenne en 2016.
Commentaire (cliquer pour afficher)
On retrouve une philosophie proche des fonctions d'agrégations en SQL.
Traçons une boîte à moustaches de la répartition des 3 variables mois par mois :
fig, axes = plt.subplots(3, 1, figsize=(15, 10), sharex=True)
for var, ax in zip(['Consommation', 'Solaire', 'Vent'], axes):
sns.boxplot(data=serie_temp, x='mois', y=var, ax=ax)
ax.set_ylabel('GWh')
ax.set_title(var)
if ax != axes[-1]:
ax.set_xlabel('')
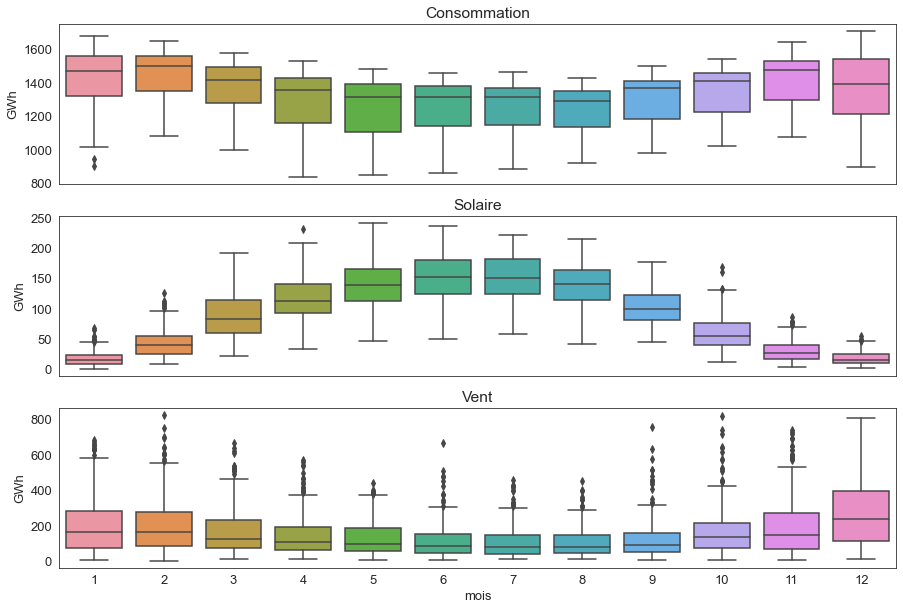
On observe que :
- les trois graphes présentent bien une variabilité saisonnière ; la consommation électrique est plus forte en hiver ainsi que la production éolienne (même si l’écart est moins marqué) et la production solaire est beaucoup plus importante en été.
- beaucoup de valeurs se retrouvent à l’extérieur des moustaches supérieures pour la production éolienne, ce qui est probablement dû à des périodes de fort vent.
Regardons maintenant jour par jour :
serie_temp["date"]=(serie_temp.index.strftime('%d %B'))
px.box(serie_temp,x='jour', y='Consommation',hover_data={"date"})
Pourquoi y a-t-il autant de points au-delà des moustaches les jours de semaine ?
Correction (cliquer pour afficher)
À cause des jours fériés.