Algorithmes dichotomiques
Cliquez sur cette invitation pour récupérer le repository du TP.
Recherche dichotomique
L’algorithme de recherche mis au point dans le tp1 compte dans le pire des cas autant d’étapes que l’ensemble scruté contient d’éléments.
Peut-on faire mieux ?
Dans le cas, d’un ensemble ordonné trié, la réponse est oui. On peut même faire beaucoup mieux !
Imaginons que l’on cherche une carte dans un jeu trié en ordre croissant. L’idée est de regarder d’abord au milieu du paquet. Si la carte du milieu est plus petite (repectivement plus grande) que la carte cherchée, on en déduit que celle-ci ne peut être que dans la deuxième partie (respectivement dans la première partie) du paquet (si elle est bien présente).
On peut alors se débarrasser de la moitié des cartes environ et on recommence la manœuvre avec les cartes restantes.
Voilà ci-dessous une tentative d’implémentation de cet algorithme :
def recherche_dicho(L,x):
n = len(L)
g, d = 0, n-1
while g < d:
i = (g + d)//2
if x < L[i]:
d = i - 1
elif x > L[i]:
g = i + 1
else:
return True
return False
Commentaire (cliquer pour afficher)
Attention à ne pas confondre avec recherche_dico du TP1, il ne s'agit pas ici de dictionnaires, mais de dichotomie...
Testez cet algorithme et constatez qu’il contient une erreur.
Recopier ci-dessous une liste triée et un élément à rechercher qui mettent en échec l’algorithme.
Correction (cliquer pour afficher)
On peut trouver de telles listes sans réfléchir en utilisant le code suivant :Si on donne la listefrom random import randint for k in range(20): L = [randint(1,10) for i in range(5)] L = sorted(L) x = randint(1,10) a = recherche_dicho(L,x) b = x in L if not ((not a and not b) or (a and b)): print(a,b,x,L)[2, 5, 7, 7, 8]en argument, la fonction renverraFalsesi on lui demande de rechercher5.
Corrigez l’algorithme
recherche_dicho_corren ajoutant un seul caractère.
Attention, tout autre ajout, même un espace, rendra faux l’exercice.
Correction (cliquer pour afficher)
Il suffit d'ajouter un=dans la condition de la bouclewhile:
while g <= d:
Commentaire (cliquer pour afficher)
Voyons pourquoi ça ne marche pas sans la correction dans le cas du contre-exemple donné :
recherche_dicho([2, 5, 7, 7, 8],5)Sans la correction, on sort de la boucle
- initialisation : $g\leftarrow 0$, $d\leftarrow 5$
- itération 1 : $i\leftarrow 2$,
L[i]vaut $7$ et donc, $d\leftarrow 1$ (on est dans leif)- itération 2 : $i\leftarrow 0$,
L[0]vaut $2$ et donc, $g\leftarrow 1$ (on est dans leelif)whileà ce moment. La fonction retourne donc à tortFalse.
Avec la correction, on fait un nouveau tour dans la boucle :
- itération 3 : $i\leftarrow 1$,
L[1]vaut $5$ et on est donc dans leelse$\Rightarrow$ la fonction retourneTrue
La figure suivante est un arbre binaire décrivant tous les chemins possibles que prend l’algorithme à partir d’une liste de 16 éléments (en vert, le nombre d’éléments restant).
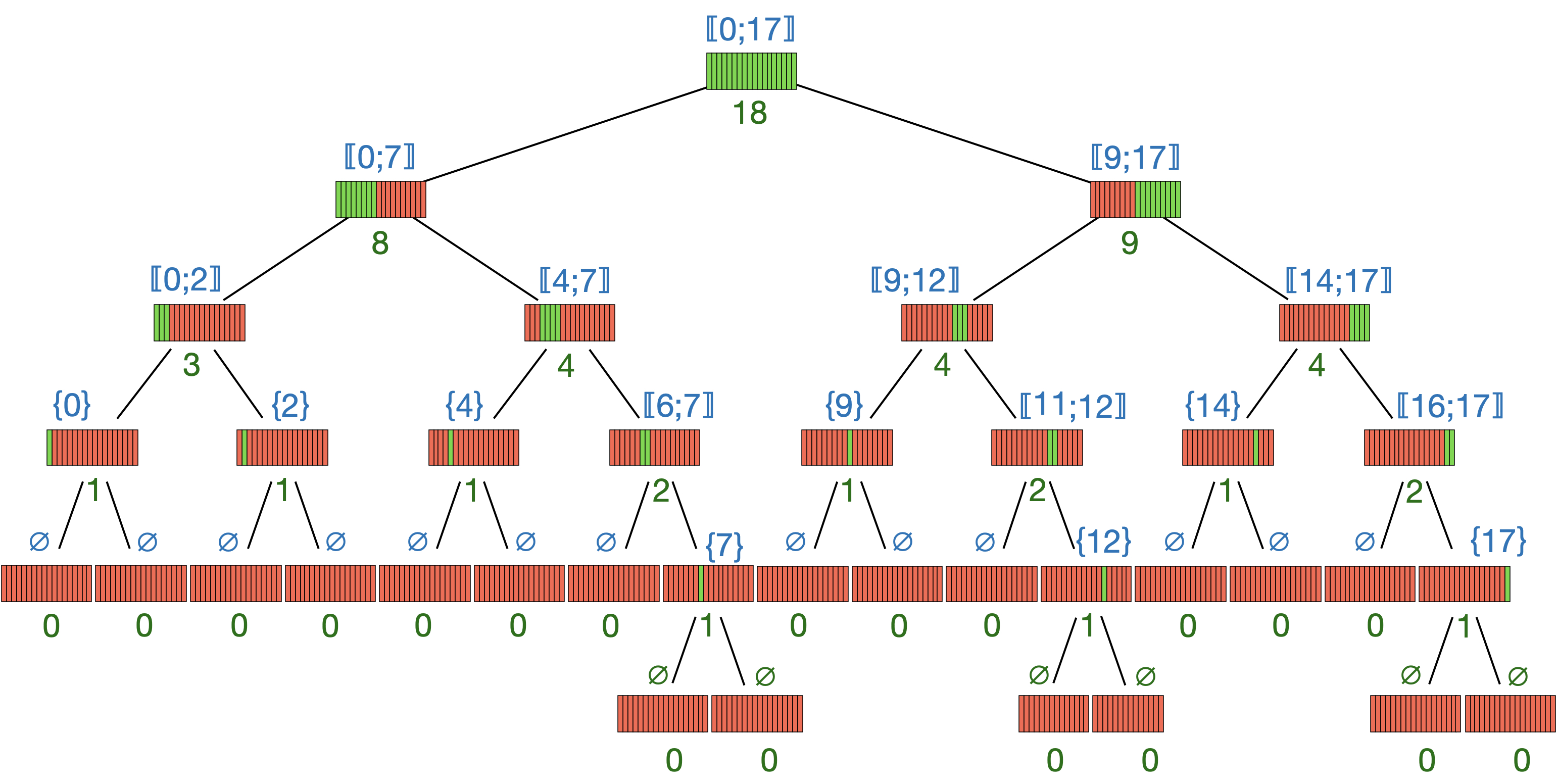
Cet algorithme peut se montrer bien plus rapide que la recherche simple du TP1.
Réouvrons la liste de mots de passe du TP2 mais en la transformant en liste de mots plutôt qu’en long texte.
# importation de la classique liste de mots de passe rockyou (cela prend quelques secondes)
from urllib.request import urlopen
url = 'http://cordier-phychi.toile-libre.org/Info/github/rockyou.txt'
rockyou = urlopen(url).read().decode('latin-1').split()
rockyou = sorted(rockyou)
print(len(rockyou),'mots de passe')
14445388 mots de passe
def trouve_indice(L, x):
'''
trouve_indice(L: liste, x: type des éléments de L) -> soit un entier, soit un booléen
postcondition: renvoie l'indice d'un éléments x lorsqu'il est présent dans la liste L
et renvoie False lorsqu'il est absent
'''
for indice, element in enumerate(L):
if element == x:
return indice
return False
Rq : enumerate est une fonction native plutôt pratique (mais en rien indispensable et d’ailleurs pas au programme).
Commentaire (cliquer pour afficher)
Ce n'est pas bien dur de réécrire la fonction sans utiliserenumerate:def trouve_indice(L, x): for i in range(len(L)): if L[i] == x: return i return False
from time import time
from random import randint
import matplotlib.pyplot as plt
plt.style.use('seaborn')
plt.rcParams['figure.figsize'] = (15, 6)
Indice, T_ch = [], []
liste_noms = ['567890','billgates','dollars','jklmno','pupuce','zorro']
for nom in liste_noms:
start = time()
i = trouve_indice(rockyou,nom)
stop = time()
Indice.append(i)
T_ch.append(stop-start)
print(f"{stop -start:.2e} s pour trouver '{nom}' qui est à la position {i}")
plt.plot(Indice,T_ch,'--')
plt.plot(Indice,T_ch,'o',c='C2')
plt.xlabel("Position dans la liste")
plt.ylabel("Temps pour trouver le nom (s)")
1.84e-01 s pour trouver '567890' qui est à la position 2612528
3.93e-01 s pour trouver 'billgates' qui est à la position 5584305
4.85e-01 s pour trouver 'dollars' qui est à la position 6925245
6.32e-01 s pour trouver 'jklmno' qui est à la position 8867150
8.32e-01 s pour trouver 'pupuce' qui est à la position 11949039
1.01e+00 s pour trouver 'zorro' qui est à la position 14416270
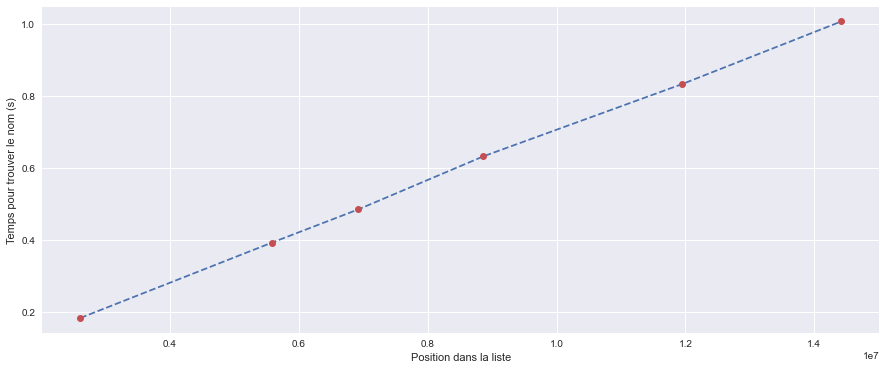
Comment semble évoluer le temps de recherche en fonction de la position dans la liste ?
Correction (cliquer pour afficher)
Le temps de recherche semble évoluer linéairement en fonction de la position dans la liste (durée $\propto$ position).
Avec l’algorithme de recherche dichotomique, on obtient :
T_ch = []
liste_noms = ['567890','billgates','dollars','jklmno','pupuce','zorro']
for i,nom in zip(Indice,liste_noms):
start = time()
recherche_dicho_corr(rockyou,nom)
stop = time()
T_ch.append(stop-start)
print(f"{stop -start:.2e} s pour trouver {nom} qui est à la position {i}")
plt.plot(Indice,T_ch,'--')
plt.plot(Indice,T_ch,'o',c='C2')
for i in range(len(liste_noms)) :
plt.text(Indice[i]+max(Indice)/100,T_ch[i],liste_noms[i])
plt.xlabel("Position dans la liste (s)")
plt.ylabel("Temps pour trouver le nom")
plt.savefig('graph.png',dpi=600)
1.41e-05 s pour trouver 567890 qui est à la position 2612528
1.41e-05 s pour trouver billgates qui est à la position 5584305
1.10e-05 s pour trouver dollars qui est à la position 6925245
2.19e-05 s pour trouver jklmno qui est à la position 8867150
1.12e-05 s pour trouver pupuce qui est à la position 11949039
1.41e-05 s pour trouver zorro qui est à la position 14416270
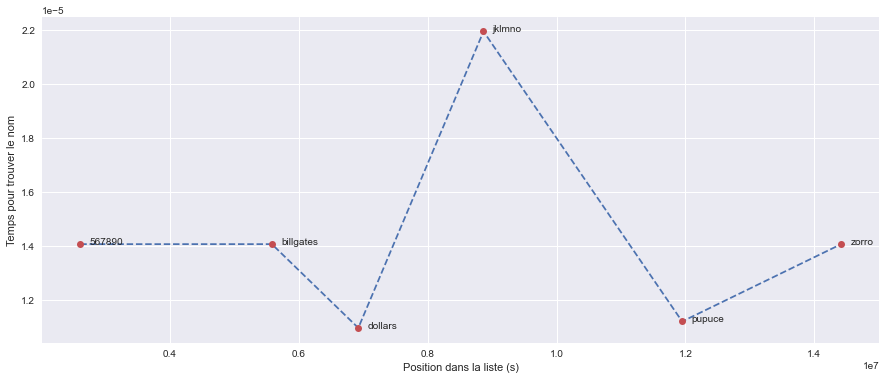
On constate que l’algorithme dichotomique met beaucoup moins de temps et qu’il ne semble pas dépendre clairement de la position de l’élément.
Tentons de comparer le comportement des deux algorithmes quand la longueur de la liste augmente.
Quel que soit l’algorithme de recherche, la pire situation possible correspond à la recherche d’un élément absent de la liste.
Se placer dans ce pire des cas permet une comparaison plus sûre des algorithmes ; on sait à quoi s’attendre !
Mesurer un temps dépend de trop de paramètres (processeur, utilisation de la mémoire par le système, etc.).
Une information plus universelle est le nombre d’étapes de l’algorithme.
Plus précisément, concentrons sur le nombre de comparaisons entre l’élément recherché x et les éléments de la liste L.
On a construit ci-dessous la fonction trouve_indice_etapes dont la description est donnée :
def trouve_indice_etapes(L,x):
"""
trouve_indice_etapes(liste: list, valeur: type des éléments de la liste) -> bool, int
postcondition: retourne à la fois un booléen qui traduit la présence ou non de l'élément
et un entier correspondant au nombre de comparaisons effectuées entre x et les éléments de L
"""
nb_comp = 0
for indice, element in enumerate(L):
nb_comp += 1
if element == valeur:
return True,nb_comp
return False,nb_comp
À vous de jouer pour construire sur le même modèle
recherche_dicho_etapes:
def recherche_dicho_etapes(L,x) :
"""
recherche_dicho_etapes(liste: list, valeur: type des éléments de la liste) -> bool, int
postcondition: doit retourner à la fois un booléen qui traduit la présence ou non de l'élément
et un entier correspondant au nombre de comparaisons effectuées entre x et les éléments de L
"""
### VOTRE CODE
Correction (cliquer pour afficher)
Il faut faire très attention aux endroits où l'on place les incrémentations denbcompdans le code derecherche_dicho.
À chaque itération, il peut y avoir soit 1 comparaison (en passant par leif), soit 2 (en passant par leelifou leelse).def recherche_dicho_etapes(L,x) : n = len(L) nb_comp = 0 g, d = 0, n-1 while g <= d: i = (g + d)//2 nb_comp += 1 # toujours au moins 1 comparaison (celle du if) if x < L[i]: d = i - 1 # pas d'incrémentation car déjà comptée elif x > L[i]: g = i + 1 nb_comp += 1 # on ajoute la comparaison du elif else: nb_comp += 1 # la comparaison du elif a été faite et elle s'est avérée fausse return True,nb_comp return False,nb_comp
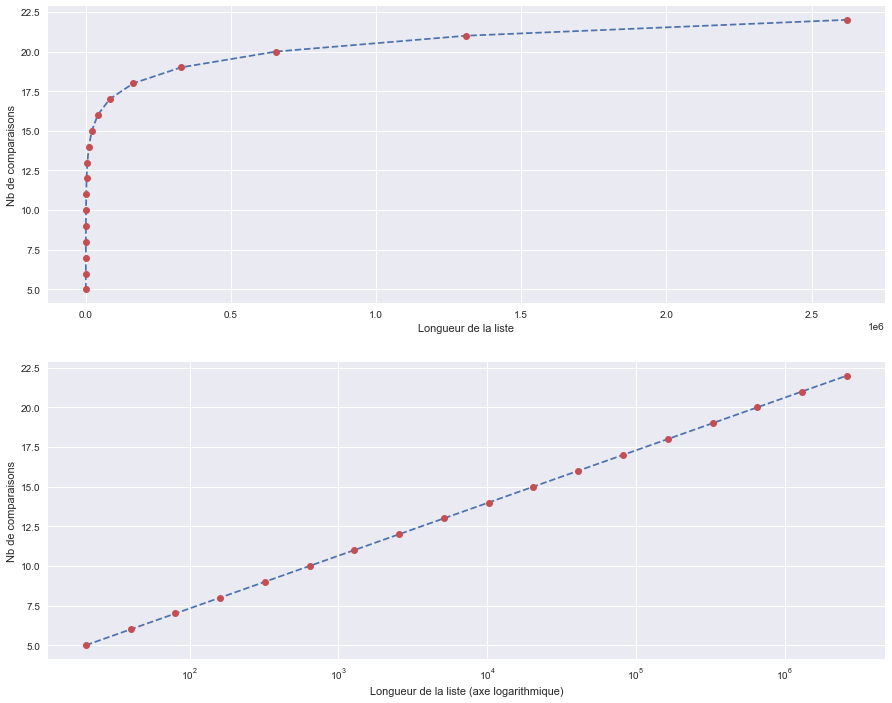
Maintenant, comparons :
import pandas as pd
NB_elts, NB_comp = [], []
nom = '???#!!!'
liste_longueurs = [10*2**i for i in range(1,19)]
for longueur in liste_longueurs:
start = time()
nb_comp = trouve_indice_etapes(rockyou[:longueur],nom)[1]
stop = time()
NB_elts.append(longueur)
NB_comp.append(nb_comp)
d = {'taille' : NB_elts,'# comparaisons': NB_comp}
tableau = pd.DataFrame(data=d)
display(tableau)
fig, axs = plt.subplots(2,figsize=(15,12))
axs[0].plot(NB_elts,NB_comp,'--')
axs[0].plot(NB_elts,NB_comp,'o',c='C2')
axs[1].semilogx(NB_elts,NB_comp,'--')
axs[1].semilogx(NB_elts,NB_comp,'o',c='C2')
axs[0].set(xlabel='Longueur de la liste', ylabel='Nb de comparaisons')
axs[1].set(xlabel='Longueur de la liste (axe logarithmique)', ylabel='Nb de comparaisons')
| taille | # comparaisons | |
|---|---|---|
| 0 | 20 | 20 |
| 1 | 40 | 40 |
| 2 | 80 | 80 |
| 3 | 160 | 160 |
| 4 | 320 | 320 |
| 5 | 640 | 640 |
| 6 | 1280 | 1280 |
| 7 | 2560 | 2560 |
| 8 | 5120 | 5120 |
| 9 | 10240 | 10240 |
| 10 | 20480 | 20480 |
| 11 | 40960 | 40960 |
| 12 | 81920 | 81920 |
| 13 | 163840 | 163840 |
| 14 | 327680 | 327680 |
| 15 | 655360 | 655360 |
| 16 | 1310720 | 1310720 |
| 17 | 2621440 | 2621440 |
NB_elts, NB_comp = [], []
nom = '???#!!!'
liste_longueurs = [10*2**i for i in range(1,19)]
for longueur in liste_longueurs:
start = time()
nb_comp = recherche_dicho_etapes(rockyou[:longueur],nom)[1]
stop = time()
NB_elts.append(longueur)
NB_comp.append(nb_comp)
d = {'taille' : NB_elts,'# comparaisons': NB_comp}
tableau = pd.DataFrame(data=d)
display(tableau)
fig, axs = plt.subplots(2,figsize=(15,12))
axs[0].plot(NB_elts,NB_comp,'--')
axs[0].plot(NB_elts,NB_comp,'o',c='C2')
axs[1].semilogx(NB_elts,NB_comp,'--')
axs[1].semilogx(NB_elts,NB_comp,'o',c='C2')
axs[0].set(xlabel='Longueur de la liste', ylabel='Nb de comparaisons')
axs[1].set(xlabel='Longueur de la liste (axe logarithmique)', ylabel='Nb de comparaisons')
| taille | # comparaisons | |
|---|---|---|
| 0 | 20 | 5 |
| 1 | 40 | 6 |
| 2 | 80 | 7 |
| 3 | 160 | 8 |
| 4 | 320 | 9 |
| 5 | 640 | 10 |
| 6 | 1280 | 11 |
| 7 | 2560 | 12 |
| 8 | 5120 | 13 |
| 9 | 10240 | 14 |
| 10 | 20480 | 15 |
| 11 | 40960 | 16 |
| 12 | 81920 | 17 |
| 13 | 163840 | 18 |
| 14 | 327680 | 19 |
| 15 | 655360 | 20 |
| 16 | 1310720 | 21 |
| 17 | 2621440 | 22 |
Commentaire (cliquer pour afficher)
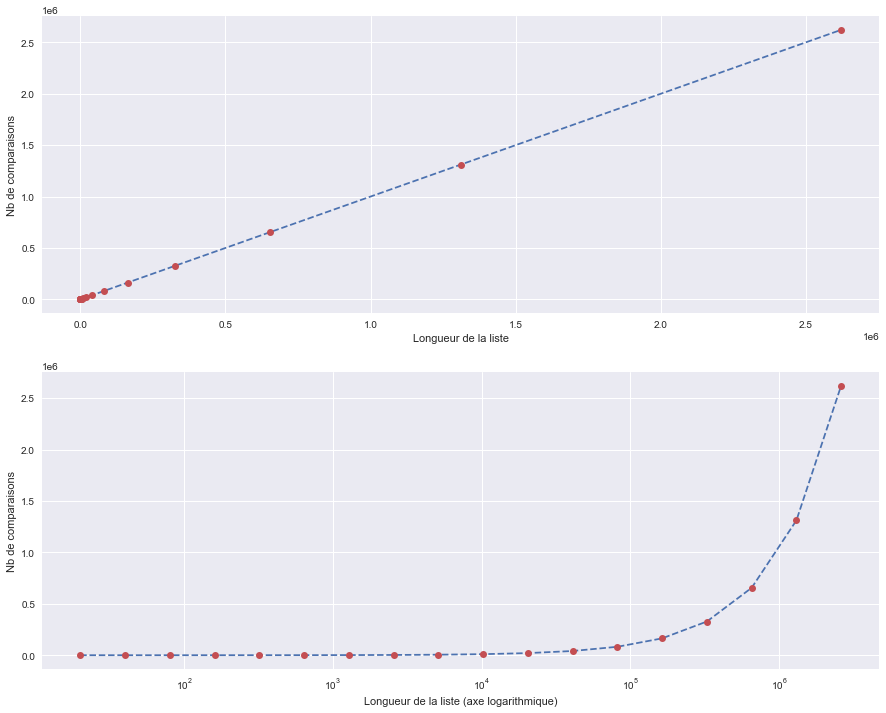
Dans le cas de la recherche linéaire, le nombre de comparaisons est proportionnel à la taille de la liste alors que dans le cas de la recherche dichotomique, le nombre de comparaisons est proportionnel au logarithme de la taille de la liste !
Recherche dichotomique d’une racine
On cherche à appliquer la méthode de la dichotomie (découpage en deux systématique d’un intervalle) à la recherche d’une racine.
Plus précisément, on souhaite déterminer une approximation d’une racine (ou zéro) sur un intervalle $[a, b]$, avec une précision $ε$, d’une fonction continue et monotone $f$ sur cet intervalle et telle que $f(a)$ et $f(b)$ sont de signes opposés ($f(a)f(b)≤0)$. Elle consiste à comparer le signe de l’image $f\left(\frac{a + b}{2}\right)$ du milieu de l’intervalle $[a, b]$ avec le signe de $f(a)$ et $f(b)$ pour réduire l’intervalle de recherche de manière itérative.
Pour déterminer $x_0$, racine de la fonction $f$, strictement monotone sur l’intervalle $[a, b]$, avec une précision $ε,$ on procède comme suit :
- On détermine le milieu de l’intervalle $m = \frac{a+b}{2}$ ;
- On compare le signe de $f(m)$ avec celui de $f(a)$ et $f(b)$ pour déterminer dans quel intervalle $[a, m]$ ou $[m, b]$ se trouve la racine $x_0$ ;
- On affecte à $a$ (resp. $b$) la valeur de $m$ si la racine se trouve entre $m$ et $b$ (resp. $a$) ;
- On itère tant que $|a − b| > ε$, (ε est la précision définie initialement), et on renvoie $m$.
Construisez une fonction
racineprenant en argument une fonctionf, les bornes d’un intervalleaetb, et une précisionepset retournant la racine ainsi que le nombre d’itérations nécessaires. Vous vous assurerez grâce à unassertqu’au moins une racine existe bel et bien dans l’intervalle choisi et vous sécuriserez la bouclewhileen ajoutant une condition empèchant l’algorithme d’utiliser plus de 100 itérations.
def racine(f,a,b,eps) :
"""
racine(f: fonction, a: flottant, b: flottant, eps: flottant) -> racine: flottant, nbiter: entier
précondition: f doit être une fonction n'ayant qu'un argument (un flottant) et ne retournant qu'un flottant.
"""
### BEGIN SOLUTION
Correction (cliquer pour afficher)
def racine(f,a,b,eps): assert f(a)*f(b)<0 nbiter = 1 nbitermax = 100 m = (a + b)/ 2 while abs(a - b) > eps and nbiter < nbitermax: # condition de convergence + non-dépassement d'un nombre limite d'iterations m = (a + b)/ 2 if f(a) * f(m) < 0: b = m else: a = m nbiter += 1 return m, nbiter
Comment évolue l’accroissement du nombre d’iterations en fonction de l’accroissement du nombre de chiffres significatifs obtenus pour la racine ?
Correction (cliquer pour afficher)
Traçons cette évolution grâce au code suivant :On obtient :def f(x): return x**2-2 Leps, Let = [], [] for i in range(1,15): eps = 10**(-i) Leps.append(1+i) nb_etapes = racine(f,1,2,eps)[1] Let.append(nb_etapes) plt.plot(Leps,Let,'--') plt.plot(Leps,Let,'o',c='C2') plt.xlabel("Nombre de chiffres significatifs") plt.ylabel("Nombre d'étapes")
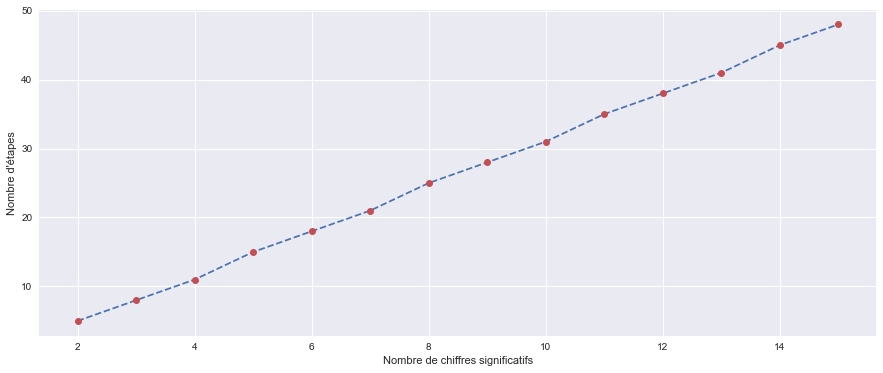
i+1correspond bien ici au nombre de chiffres significatifs souhaités puisque la solution, 1,414..., ne contient qu'un seul chiffre avant la virgule.
On constate que l'accroissement du nombre d'itérations semble proportionnel à l'accroissement du nombre de chiffres significatifs souhaité.