Fonctions récursives
Cliquez sur cette invitation pour récupérer le repository du TP.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
plt.style.use('seaborn')
plt.rcParams['figure.figsize'] = (10, 10)
fig, ax = plt.subplots()
ax.set_aspect(1)
couleurs = plt.rcParams['axes.prop_cycle'].by_key()['color']
Visualisation des appels récursifs
Installons un module permettant de représenter sous forme de graphe les différents appels récursifs d’une fonction.
%%capture
!pip install recursionvisualisation==0.2
On construit une fonction récursive somme(n) qui retourne la somme des n premiers entiers et on utilise un décorateur (fonction qui modifie le comportement d’autres fonctions) pour visualiser les différents appels récursifs faits par somme.
from recursionvisualisation import viz, CallGraph
cg = CallGraph()
@viz(cg) # décorateur
def somme(n):
if n < 1:
return 0
return n + somme(n - 1)
print(f'somme(5) = {somme(5)}')
cg.render()
somme(5) = 15

On observe l’empilement des appels successifs de somme jusqu’à ce que le cas de base soit touché. Ces appels forment une pile d’exécution (ou pile d’appels, “call stack” en anglais).
Le cas de base correspond à la première valeur retournée (0 ici) et donc au premier appel retiré de la pile. Tous les appels précédents sont restés en attente.
On remonte ensuite chronologiquement la pile des appels avec à chaque fois une nouvelle valeur retournée, jusqu’à l’appel initial, appelé appel terminal.
Combien l’expression
somme(100)va-t-elle provoquer d’appels de la fonctionsomme?
Correction (cliquer pour afficher)
101
Les choses se compliquent si plusieurs appels récursifs sont faits dans la définition de la fonction.
Le nombre d’appels progresse maintenant exponentiellement mais pas la taille de la pile d’exécution qui correspond au nombre de niveaux (à la profondeur de l’arbre).
cg = CallGraph()
@viz(cg)
def fib(n):
if n < 2:
return n
return fib(n-1) + fib(n-2)
print(f'{fib(5) = }')
cg.render()
fib(5) = 5
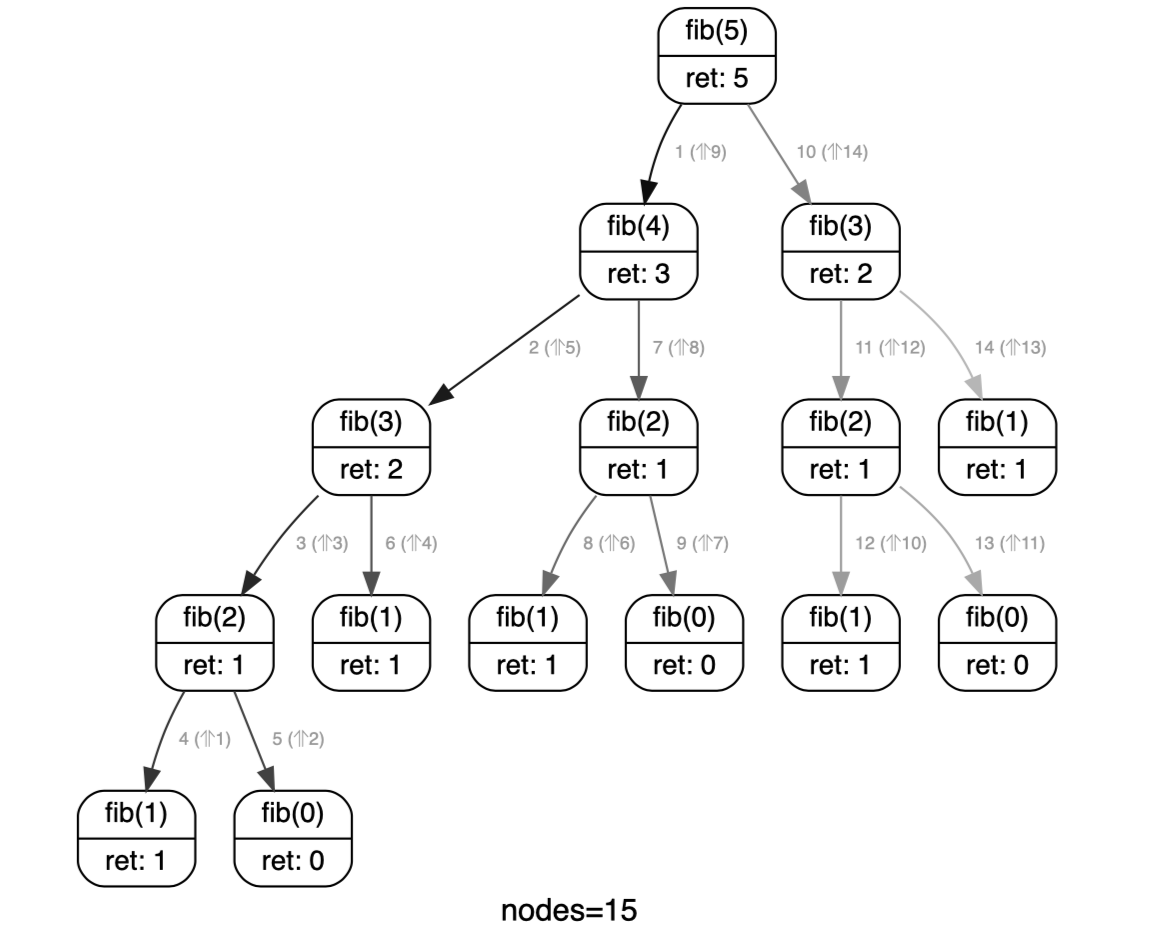
Comme on le voit ci-dessus, fib(5) fait 15 appels à la fonction mais la pile ne dépasse jamais 6 appels en attente.
En effet, fib(5) appelle fib(4) qui appelle fib(3)qui appelle fib(2) qui appelle fib(1). Comme fib(1) est un des deux cas de base possible, il retourne la valeur 1 et est retiré de la pile. Le dernier appel en attente de la pile est alors fib(2), on y retourne.
fib(2) fait son deuxième appel : fib(0). fib(0) étant l’autre cas de base, il retourne une valeur (0) et est retiré de la pile. fib(2) peut maintenant elle aussi retourner une valeur (1+0) et est à son tour retirée de la pile.
Le dernier appel en attente est dorénavant fib(3) qui fait maintenant son deuxième appel : fib(1). fib(1) retourne 1 et est retiré de la liste, fib(2) retourne 2 (1+1) et est retirée à son tour, et on remonte à fib(4) qui fait son deuxième appel, fib(2), qui elle-même appelle fib(1), etc.
Quelle sera la taille maximale de la pile d’exécution de
fib(100)?
Correction (cliquer pour afficher)
100
Commentaire (cliquer pour afficher)
Par contre, le nombre d'appels est bien plus grand (cf. vidéo).
Deux tris récursifs
Construisons les deux tris récursifs présentés dans la vidéo.
Tri insertion
Écrire la fonction
insertionqui insert au bon endroit un nombre dans une liste triée afin qu’elle reste triée.
def insertion(element,Ltriee):
"""
insertion(element: nombre, Ltriee: liste de nombres) -> Lsortie: liste de nombres
insertion insert 'nombre' au bon endroit dans 'Ltriee' et retourne cette nouvelle liste.
préconditions: 'element' est un entier ou un flottant, 'Ltriee' est une liste de nombres triée en ordre croissant
postconditions: 'Lsortie' est triée dans l'ordre croissant (et len(Lsortie)==len(Ltriee)+1)
"""
### VOTRE CODE
Exemple : insertion(5,[-12,1e-2,0,3,18]) doit renvoyer [-12,1e-2,0,3,5,18] .
Correction (cliquer pour afficher)
def insertion(element,Ltriee): i = 0 while i < len(Ltriee) and element > Ltriee[i]: #inverser les deux conditions provoque une erreur (caractère paresseux de and) i += 1 Lsortie = Ltriee[:i]+[element]+Ltriee[i:] return Lsortie
Combien d’itérations sont nécessaires dans le pire des cas pour insérer un élément dans une liste de longueur
n?
- A : $n$
- B : $2n$
- C : $n^2$
Correction (cliquer pour afficher)
$n$
Ajouter le cas de base à la fonction
tri_insertion:
def tri_insertion(liste) :
n = len(liste)
### VOTRE CODE
else :
element = liste[0]
reste = liste[1:]
return insertion(element,tri_insertion(reste))
# si pas de return dans le else alors tous les appels de tri_insertion avec un len > 1 sont de type None !!!
Correction (cliquer pour afficher)
def tri_insertion(liste) : n = len(liste) if n == 1 or n == 0 : # cas de base return liste else : element = liste[0] reste = liste[1:] return insertion(element,tri_insertion(reste))
Combien d’appels à
tri_insertionsont faits au sein detri_insertion(L)quandLà une taillen?
- A : $n-1$
- B : $2^n$
- C : $\log_2(n)$
Correction (cliquer pour afficher)
$n-1$
Tri fusion
Écrire la fonction
fusionqui fusionne deux listes triées en une seule liste triée.
def fusion(Ltrie1,Ltrie2):
"""
fusion(Ltrie1: liste de nombres, Ltrie2: liste de nombres) -> liste_sortie: liste de nombres
fusion retourne une seule liste ordonnée à partir de deux sous-listes ordonnées.
préconditions: Ltrie1 et Ltrie2 sont triées dans l'ordre croissant.
postconditions: 'Lfus' est triée dans l'ordre croissant (et len(Lfus)==len(Ltrie1)+len(Ltrie2)).
"""
### VOTRE CODE
Exemple : fusion([-12,3.5,18],[-2,15]) doit renvoyer [-12,-2,3.5,15,18].
Correction (cliquer pour afficher)
def fusion(Ltrie1,Ltrie2) : if Ltrie1 == []: return Ltrie2 elif Ltrie2 == []: return Ltrie1 elif Ltrie1[0] <= Ltrie2[0]: return [Ltrie1[0]] + fusion(Ltrie1[1:],Ltrie2) else: return [Ltrie2[0]] + fusion(Ltrie1,Ltrie2[1:])
Compléter la définition de
tri_fusionpour le rendre opérant. Il faut que chaque appel récursif concerne approximativement une moitié de la liste.
def tri_fusion(L):
n = len(L)
if n == 1:
return L
else:
L = fusion(trifusion(L[...]),trifusion(L[...]))
return L
Correction (cliquer pour afficher)
Un découpage en deux parties approximativement égales de la liste est obtenu parL[:n//2]etL[n//2:].
On écrit donc :
L = fusion(trifusion(L[:n//2]),trifusion(L[n//2:]))
Supposons que la longueur de la liste L soit une puissance de 2.
Au niveau de récursivité $j$ (à l’appel initial de tri_fusion(L), $j=0$, pour les deux appels à tri_fusion au sein de tri_fusion(L), $j=1$, etc.), on a décomposé le problème initial en … fusions, chacune opérant sur des sous-listes de taille … .
Par quoi faut-il compléter les pointillés respectivement ?
- A : $2^j$ et $2^j$
- B : $n/2^j$ et $n/2^j$
- C : $2^j$ et $n/2^j$
- D : $n/2^j$ et $2^j$
Correction (cliquer pour afficher)
On a décomposé le problème initial en $2^j$ fusions, chacune opérant sur des sous-listes de taille $n/2^j$.
Algorithme d’Euclide
Un des plus vieux algorithmes connus, l’algorithme d’Euclide, suit un raisonnement récursif et s’écrit donc naturellement de cette façon.
Principe de l’algorithme : le plus grand commun divisieur (pgcd) entre deux nombres a et b est le même que celui entre b et le reste de la division euclidienne de a par b ($a\pmod b$). Algébriquement, cela donne $\text{pgcd}(a,b)=\text{pgcd}(b,a\pmod b)$.
On a donc ainsi réduit le problème initial en un problème plus simple, ce qui permet d’appliquer la technique algorithmique diviser pour régner.
Écrivez une fonction récursive
pgcdpermettant de calculer le pgcd entre deux nombres (n’oubliez pas le cas de base qu’il vous faudra déterminer).
def pgcd(a,b):
"""
pgcd(a: int,b: int) -> int
"""
### VOTRE CODE
Correction (cliquer pour afficher)
def pgcd(a,b): if b == 0: return a else: return pgcd(b,a%b)
pgcd(1080,480)
120
Commentaire (cliquer pour afficher)
Une petite vidéo sur l'algorithme d'Euclide :
Une utilité géométrique du pgcd : le pavage d’un rectangle par les plus grands carrés possibles.
ax.clear()
a = 1080
b = 480
ax.set_xlim([0, a])
ax.set_ylim([0, b])
ax.add_patch(Rectangle((0,0), a, b, color='white'))
# Le côté du plus gros carré pavant le rectangle de longueur a et largeur b vaut pgcd(a,b) !
for i in range(a//pgcd(a,b)) : # a//pgcd(a,b) : nombre de carrés dans la longueur
for j in range(b//pgcd(a,b)) : # b//pgcd(a,b) : nombre de carrés dans la largeur
ax.add_patch(Rectangle((pgcd(a,b)*i, pgcd(a,b)*j), pgcd(a,b), pgcd(a,b),color=couleurs[(i+j)%2]))
fig
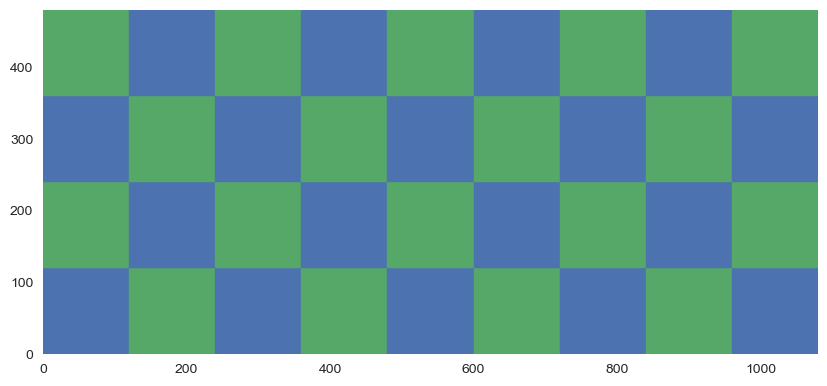
Commentaire (cliquer pour afficher)
Une vidéo un peu chargée sur la complexité de l'algorithme d'Euclide :
Dessins récursifs
def dessine_cercle(centre,rayon) :
theta = np.linspace(0, 2*np.pi, 100) # permet d'avoir 100 valeurs entre 0 et 2pi
x0,y0 = centre
x = rayon*np.cos(theta)+x0
y = rayon*np.sin(theta)+y0
ax.plot(x, y)
ax.fill(x, y)
return fig
ax.clear()
dessine_cercle((4,6),5) # cercle de centre (4,6) et de rayon 5
def cercles(centre,rayon) :
dessine_cercle(centre,rayon)
if rayon > 0.1 :
cercles(centre,rayon*0.9)
return fig
ax.clear()
cercles((10,10),20)
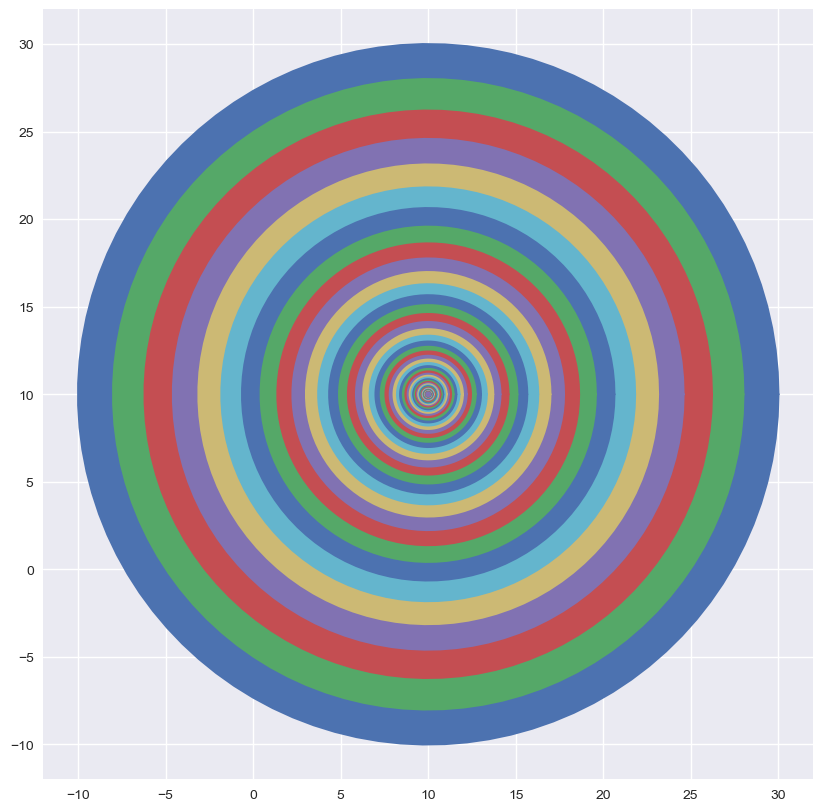
Définir une fonction récursive
dessinqui affiche l’image ci-dessous avec l’appeldessin((0,0),20).
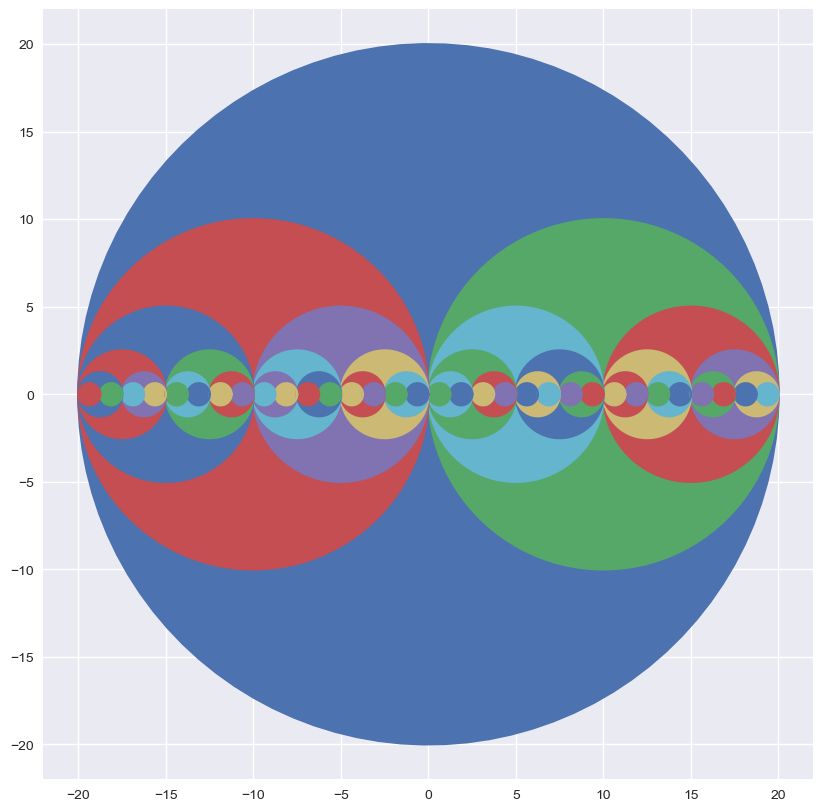
def dessin(centre,rayon):
### VOTRE CODE
return fig
Correction (cliquer pour afficher)
def dessin(centre,rayon): dessine_cercle(centre,rayon) if rayon > 1: x,y = centre dessin((x+rayon/2,y),rayon/2) dessin((x-rayon/2,y),rayon/2) return fig
# La figure qui s'affiche en exécutant cette cellule doit être identique à l'image précédente.
ax.clear()
dessin((0,0),20)
L-système (système de Lindenmayer)
plt.rcParams['figure.figsize'] = (7, 7)
ax.clear()
Pour tracer une ligne brisée allant du point $\left(0;0\right)$ au point $\left(2;0\right)$ en passant par le point $\left(1;1\right)$ avec matplotlib, on peut faire l’appel suivant à plot :
ax.plot([0, 1, 2], [0, 1, 0])
# [0, 1, 2] sont les valeurs des x
# et [0, 1, 0] sont les valeurs des y
fig
Comme c’est plus courant de penser en termes de coordonnées, on va construire une fonction dessine_points qui permet de tracer des lignes joignant une liste de points donnés sous le format (x,y).
Complétez la définition de
dessine_pointsci-dessous.
def dessine_points(liste_points):
"""
précondition: liste_points est une liste de tuples contenant chacun deux nombres (x1,y1),(x2,y2),etc.
"""
### VOTRE CODE
ax.plot(X,Y)
return fig
Correction (cliquer pour afficher)
def dessine_points(liste_points): X = [M[0] for M in liste_points] Y = [M[1] for M in liste_points] ax.plot(X,Y) return fig
# les instructions suivantes doivent afficher le même graphe que plus haut.
ax.clear()
dessine_points([(0,0),(1,1),(2,0)])

Le “graphisme tortue” est un style de graphique où on commande le crayon en vue subjective ; on bouge un curseur (la tortue) sur le plan cartésien en retenant systématiquement sa position et sa direction actuelles (où est la tortue et vers où elle est tournée).
Dans la suite, on va faire en sorte de pouvoir envoyer trois ordres à la tortue codés chacun par un caractère :
'A': avance d’une certaine longueur dans ta direction actuelle'+': tourne dans le sens des aiguilles d’une montre d’un certain angle sans avancer'-': tourne dans le sens inverse des aiguilles d’une montre d’un certain angle sans avancer
On va donc devoir convertir une suite de consignes comme 'A+A-A+A-A' en une liste de points.
from math import pi, sin, cos
Compléter la définition de
consigne_vers_pointsde façon à ce que le nouveau point(x_new,y_new)corresponde à une tortue ayant avancé de la distanceDdans la direction actuelle depuis(x_old,y_old)(il manque seulement la définition dey_new).
def consigne_vers_points(consigne,angle):
"""
consigne_vers_points(consigne: string) -> liste_de_points: list
precondition: angle est donné en radian
postcondition: liste_de_points est une liste de tuples contenant chacun deux nombres
"""
liste_de_points = [(0,0)] # point de départ
D = 1 # distance de laquelle la tortue avance à chaque F
direction = 0 # direction initiale de la tortue (vers la droite)
for c in consigne:
x_old,y_old = liste_de_points[-1]
if c == 'A':
# création de x_new et y_new
x_new = x_old + D*cos(direction)
### VOTRE CODE
liste_de_points.append((x_new,y_new))
elif c == '+':
direction -= angle
elif c == '-':
direction += angle
return liste_de_points
Correction (cliquer pour afficher)
Il manque la définition dey_new:
y_new = y_old + D*sin(direction)
L’exécution des deux lignes suivantes doit afficher le graphe ci-dessous.
ax.clear()
dessine_points(consigne_vers_points('A-A+A--A-A',pi/4))
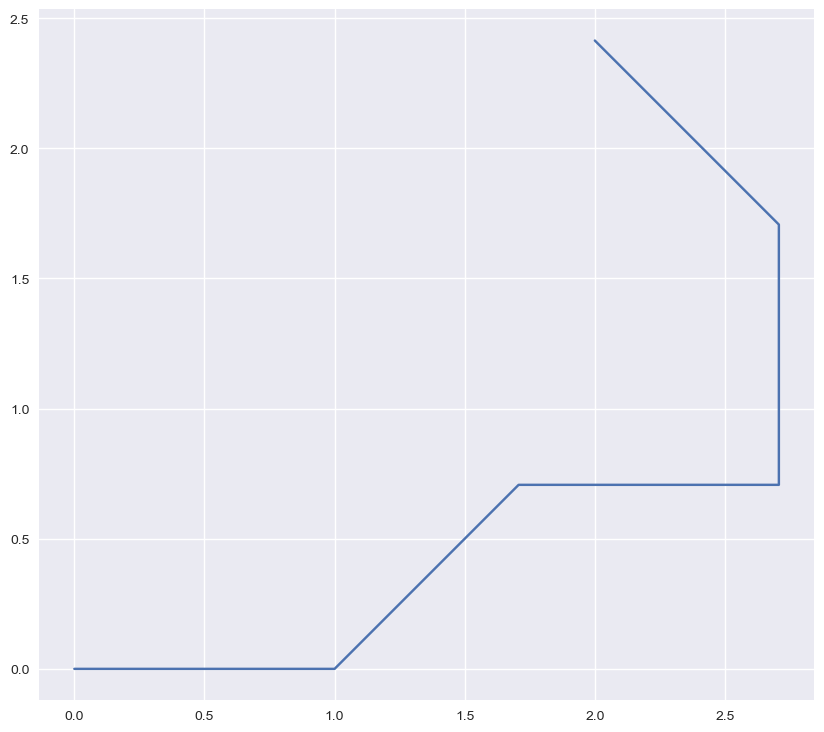
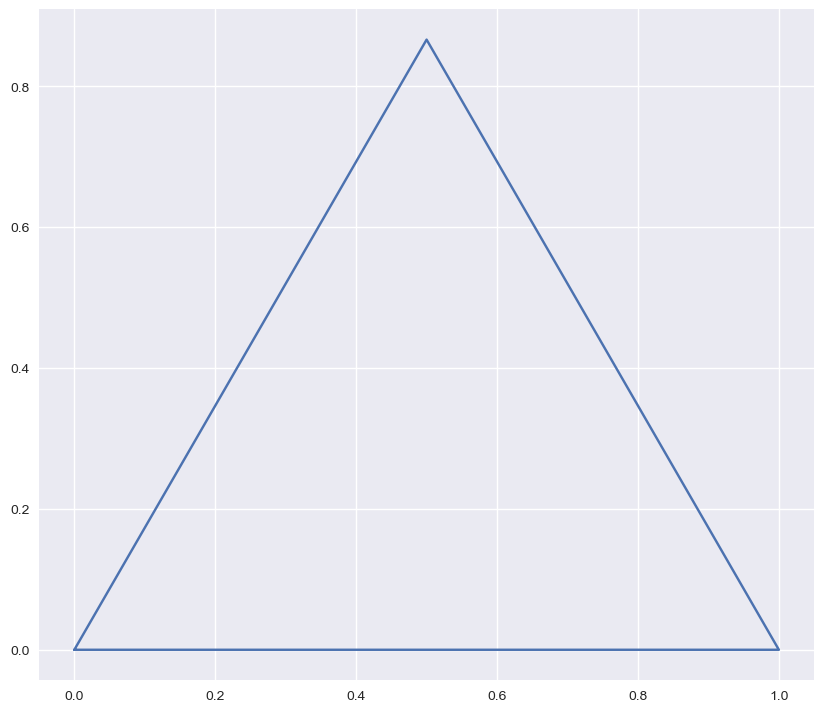
Donner la consigne et l’angle permettant de tracer le triangle équilatéral suivant (votre consigne ne devra comprendre que 5 caractères !) :
ax.clear()
consigne = '...'
angle = 0
dessine_points(consigne_vers_points(consigne,angle))
Correction (cliquer pour afficher)
consigne = 'A-A-A'
angle = 2*pi/3
Ajoutons un jeu de règles capables de transformer une chaîne de caractères.
Imaginons la séquence ‘abca’ et les règles suivantes :
'a'->'b''b'->'aba'
Alors la séquence ‘abca’ transformée par la règle devient ‘babacb’ (‘c’ n’étant pas touché par la règle, il n’est pas modifié).
Construisez une fonction
transformationprenant en argumant une chaîne de caractères appelée axiome et une règle donnée sous la forme d’un dictionnaire et retournant la séquence transformée.
Pour la règle de notre exemple, le dictionnaire serait{'a':'b','b':'aba'}.
def transformation(axiome,regle):
"""
transformation(axiome: string, regle: dictionnary) -> nvelle_chaine: string
"""
### VOTRE CODE
axiome = 'abca'
regle = {'a':'b','b':'aba'}
transformation(axiome,regle)
Doit donner 'babacb'.
Correction (cliquer pour afficher)
def transformation(axiome,regle): nvelle_chaine = '' for car in axiome: if car in regle: nvelle_chaine += regle[car] else: nvelle_chaine += car return nvelle_chaine
Faisons maintenant en sorte de pouvoir appliquer la transformation à elle-même :
- si le niveau de récursivité vaut zéro, on retourne juste l’axiome,
- sinon, on retourne le résultat de la transformation appliquée non plus sur l’axiome, mais sur la transformation de l’axiome par la règle, et on diminue le niveau d’une unité (il faut nécessairement faire en sorte d’atterrir sur le cas de base).
Complétez la définition de la fonction ci-dessous et testez-la dans la cellule suivante (il ne manque que l’appel récursif).
def transformation_recu(axiome,regle,niveau):
"""
transformation_recu(axiome: string, regle: dictionnary, niveau: int) -> nvelle_chaine: string
precondition: niveau doit être un entier positif !
"""
if niveau > 0 :
return transformation_recu(...,...,...)
else :
nvelle_chaine = axiome
return nvelle_chaine
Correction (cliquer pour afficher)
On complète les arguments detransformation_recu:
transformation_recu(transformation(axiome,regle),regle,niveau-1)
axiome = 'aba'
regle = {'a':'b','b':'aba'}
for i in range(6):
print(transformation_recu(axiome,regle,i))
#doit s'afficher :
#aba
#babab
#abababababa
#babababababababababab
#abababababababababababababababababababababa
#babababababababababababababababababababababababababababababababababababababababababab
À partir d’un axiome, d’une règle de transformation, et de l’application récursive de la transformation sur l’axiome, on obtient une consigne permettant de faire dessiner des fractales à la tortue !
Pour le flacon de Koch, on part d’un triangle équilatéral comme axiome (construit à partir d’un angle de π/3 pour les virages de la tortue), et pour chaque segment de droite, on suit la règle de transformation représentée dans le schéma suivant.
À vous de déterminer l’axiome et la bonne règle.
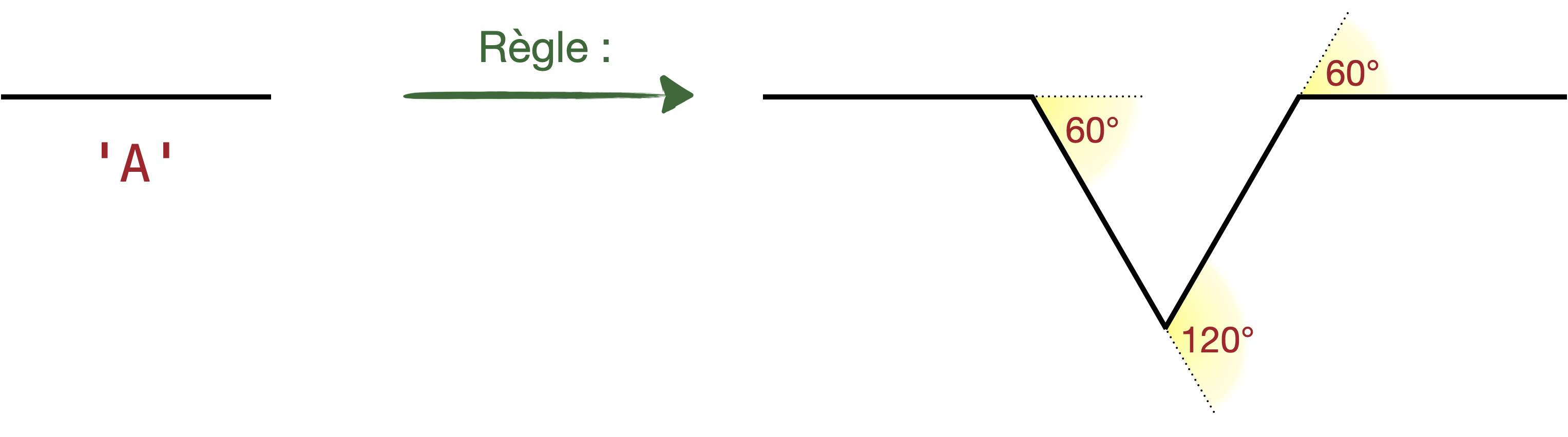
axiome = '...'
regle_Koch = {'A':'...'}
Correction (cliquer pour afficher)
axiome = 'A--A--A'
regle_Koch = {'A':'A+A--A+A'}
ax.clear()
dessine_points(consigne_vers_points(transformation_recu(axiome,regle_Koch,5),pi/3))
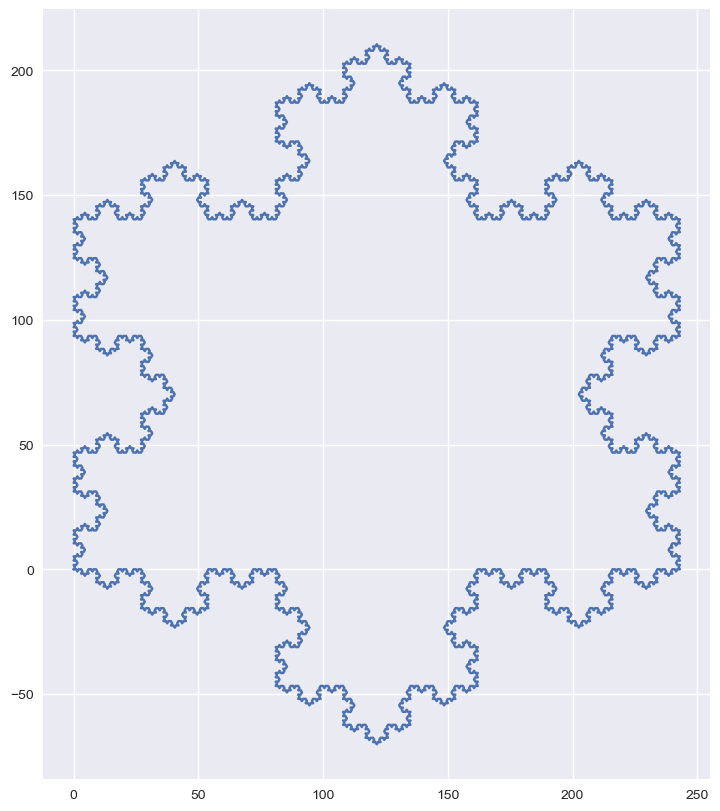
Autre exemple : comment construire une surface 2D à partir d’une courbe 1D avec la courbe de Hilbert.
axiome = 'L'
regle_Hilbert = {'L':'-RA+LAL+AR-','R': '+LA-RAR-AL+'}
ax.clear()
dessine_points(consigne_vers_points(transformation_recu(axiome,regle_Hilbert,6),pi/2))

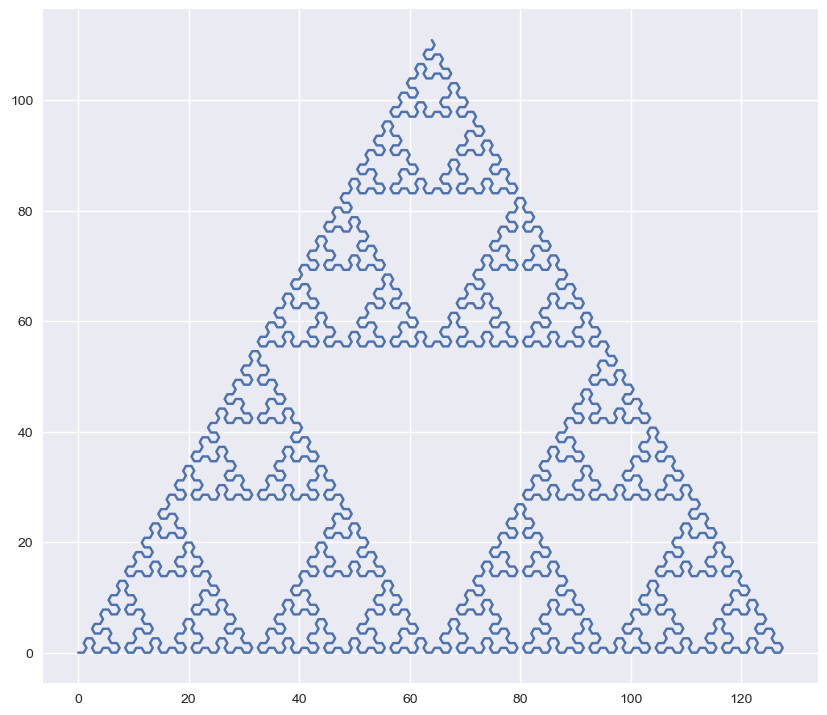
Autre exemple : un triangle de Sierpinski.
axiome = "YA"
regle = {"X":"YA+XA+Y", "Y":"XA-YA-X"}
angle = pi/3
ax.clear()
dessine_points(consigne_vers_points(transformation_recu(axiome,regle,7),angle))
Et enfin, une jolie courbe du dragon.
axiome = "AX"
regle = {"X":"X+YA+", "Y":"-AX-Y"}
angle = pi/2
ax.clear()
dessine_points(consigne_vers_points(transformation_recu(axiome,regle,16),angle))
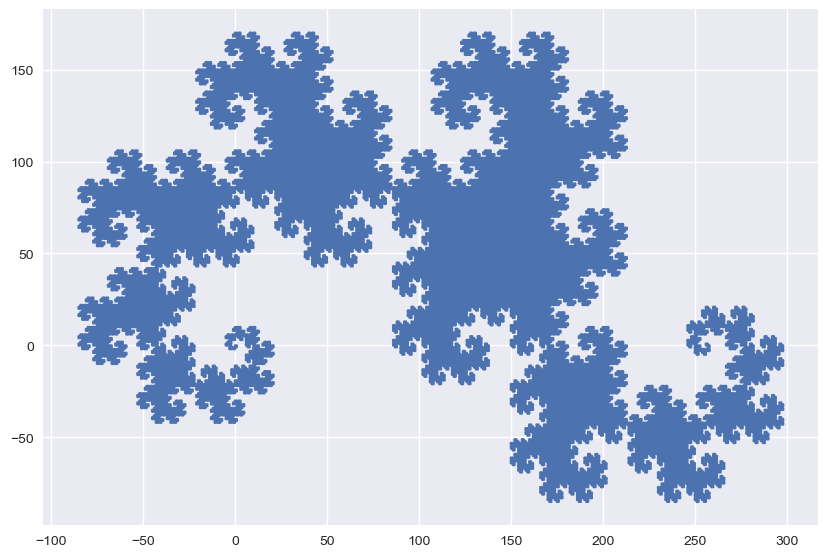
En donnant de la mémoire à la tortue, on va pouvoir dessiner des branches.
Pour cela, il faut ajouter deux nouvelles consignes à consigne_vers_points_branche :
'[': qui ajoute à une liste (la “mémoire”), la position actuelle de la tortue.']': qui permet à la tortue de retourner à la dernière position en mémoire.
Voici une implémentation possible d’une fonction consigne_vers_points_branche intégrant ces deux nouvelles consignes :
def consigne_vers_points_branche(consigne,angle):
liste_de_points = [(0,0)]
D = 1
direction = pi/2
memoire = []
for c in consigne:
x_old,y_old = liste_de_points[-1]
if c == 'A':
x_new = x_old+D*cos(direction)
y_new = y_old+D*sin(direction)
liste_de_points.append((x_new,y_new))
elif c == '+':
direction -= angle
elif c == '-':
direction += angle
elif c == '[':
memoire.append(((x_old,y_old),direction))
elif c == ']':
souvenir = memoire.pop()
x_new,y_new = souvenir[0]
direction = souvenir[1]
liste_de_points.append((float('nan'),float('nan')))
liste_de_points.append((x_new,y_new))
return liste_de_points
ax.clear()
dessine_points(consigne_vers_points_branche('A[-A]+A', pi/4))
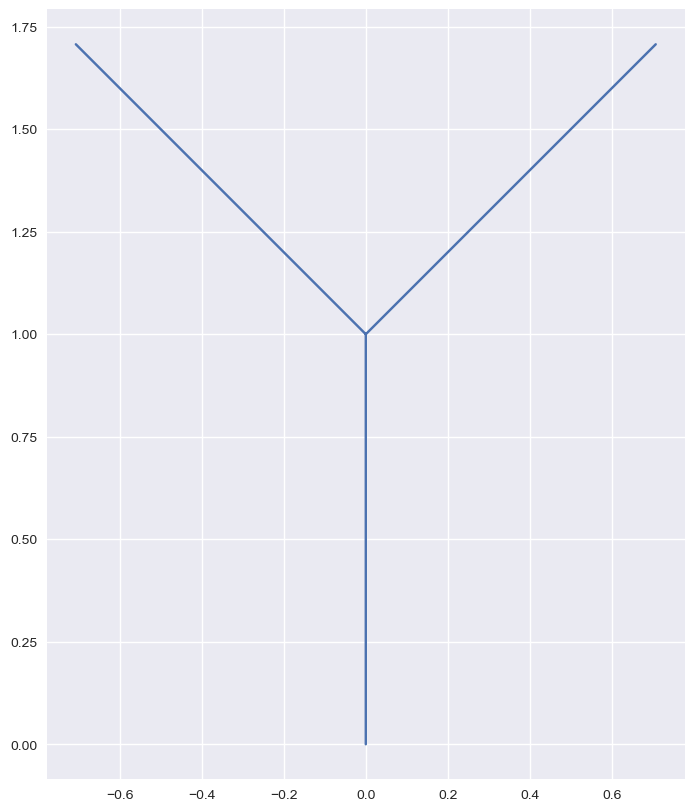
Reproduisez la figure suivante en définissant la bonne consigne et le bon angle :
ax.clear(ax.clear(`ax.clear(ax.clear(`)
consigne = '...'
angle = 0
dessine_points(consigne_vers_points_branche(consigne, angle))
draw_circle = plt.Circle((0.5, 2.7), 0.3)
ax.add_artist(draw_circle)
fig
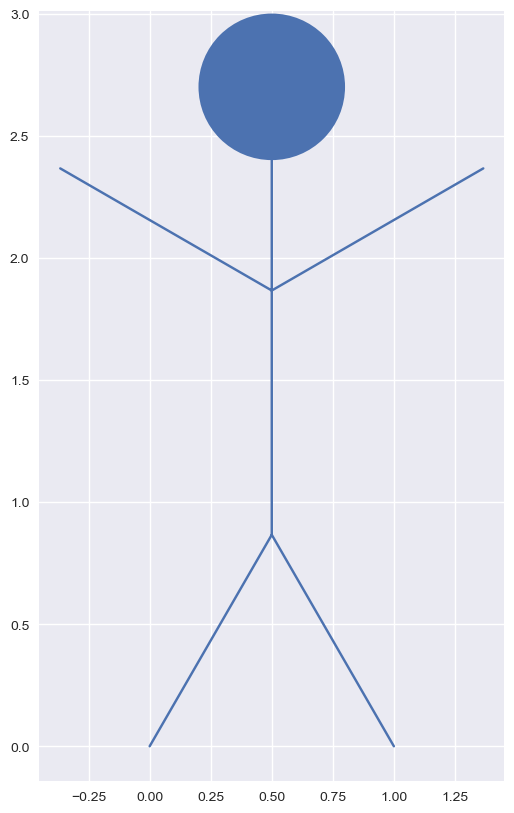
Correction (cliquer pour afficher)
consigne = '+A[++++A]-A[A][--A]++A'
angle = pi/6
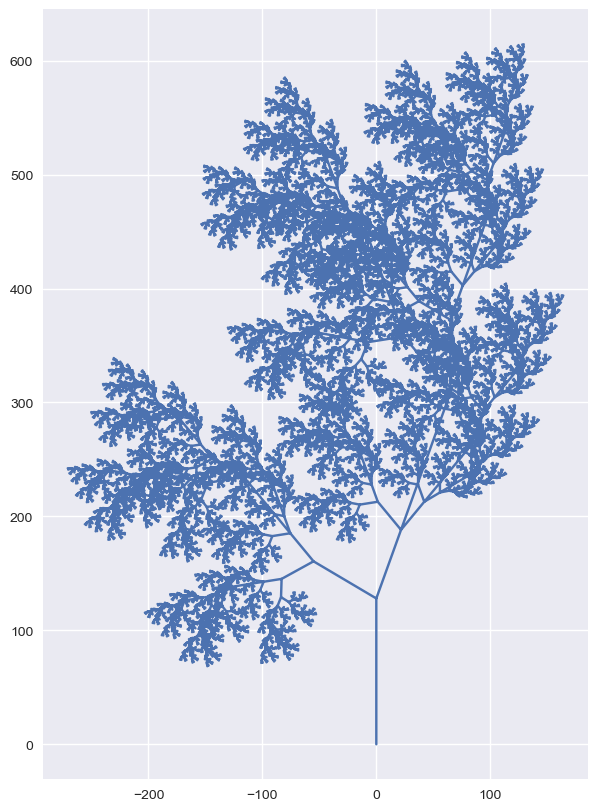
Et en utilisant la récursivité, on peut désormais dessiner de jolis arbres :
axiome = 'P'
regle = {'A': 'AA', 'P': 'A[+PA-[P]--P][---P]'}
angle = pi*0.11
ax.clear()
dessine_points(consigne_vers_points_branche(transformation_recu(axiome,regle,8),angle))