Algorithmes de tri

Cliquez sur cette invitation pour récupérer le repository du TP.

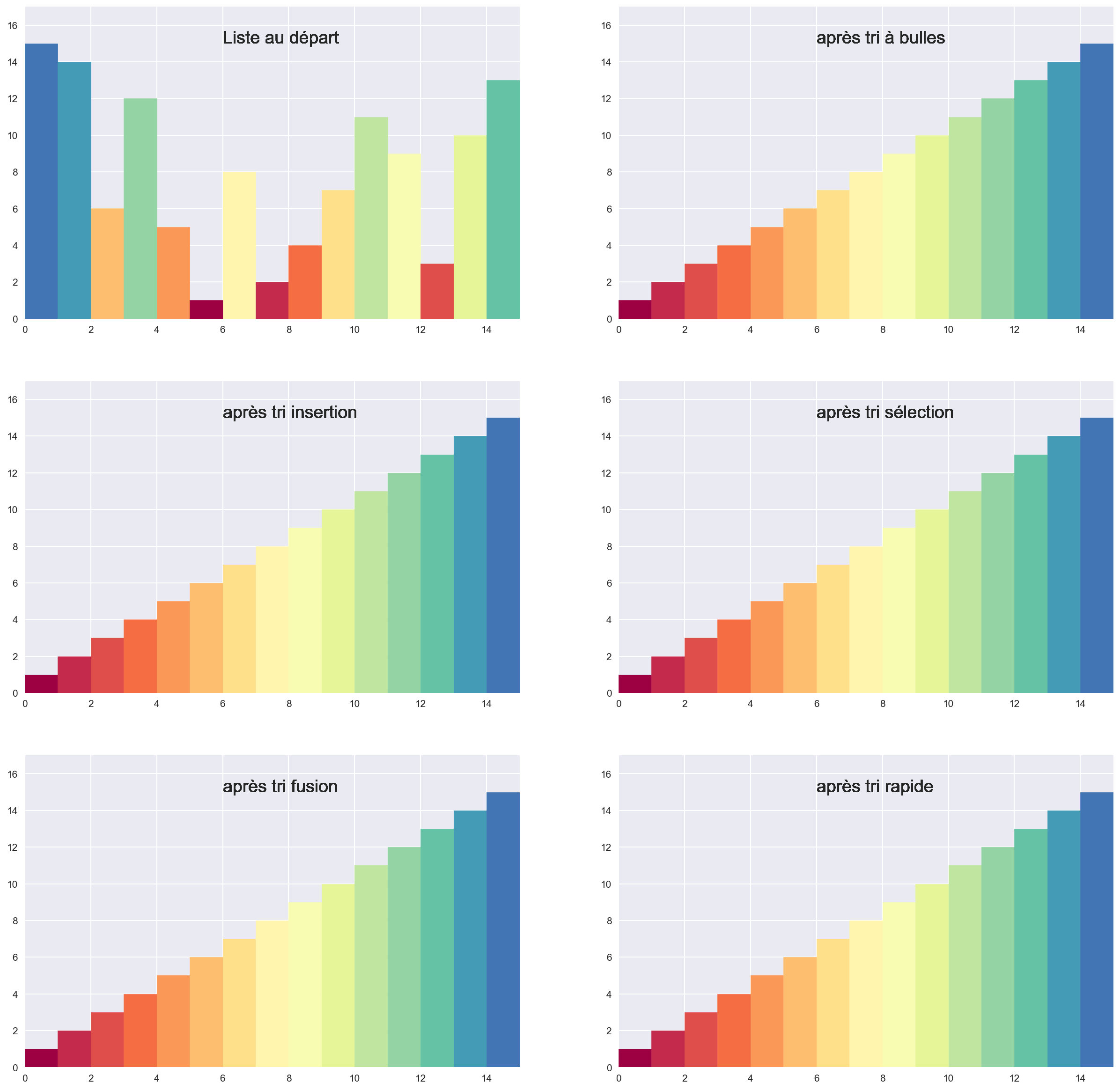
Tous ces algos de tri semblent faire correctement le boulot. Qu'est-ce qui les différencie ?

Trier c’est partir d’une structure de données désordonnée et la remettre en ordre.
Les tris sont omniprésents en informatique et Tim Roughgarden (auteur d’Algorithms illuminated) en parle même comme de la “mère de tous les problèmes algorithmiques”.
Plusieurs stratégies existent. On va en passer certaines en revue et essayer de trier les algorithmes de tri.

Tris par comparaison

La plupart des algorithmes de tri sont dits par comparaison car ils reposent sur des comparaisons deux à deux des éléments de la liste.

On a déjà rencontré deux algorithmes de tri par comparaison dans le TP sur la récursivité : le tri par insertion et le tri fusion.

Tri fusion

def fusion(L1,L2) :
    """
    fusion(L1:list,L2:list)->Lfus:list
    fusion retourne une seule liste ordonnée à partir de deux sous-listes ordonnées
    préconditions : L1 et L2 sont triée dans l'ordre croissant
    postconditions : 'Lfus' est triée dans l'ordre croissant (et len(Lfus)==len(L1)+len(L2))
    """
    if L1 == [] :
        return L2
    if L2 == [] :
        return L1
    if L1[0] <= L2[0] : # devient instable si < au lieu de <= !
        return [L1[0]] + fusion(L1[1:],L2)
    else :
        return [L2[0]] + fusion(L1,L2[1:])

def tri_fusion(L) :
    n = len(L)
    if n <= 1 :
        return L
    else :
        return fusion(tri_fusion(L[:n//2]),tri_fusion(L[n//2:]))

Combien de comparaisons entre deux éléments de la liste effectue l’algorithme de tri fusion pour ordonner [1,2,3,4,5,6,7,8] et [8,7,6,5,4,3,2,1] ?

• A : 0 et 8
• B : 8 et 16
• C : 12 et 12
• D : 16 et 8

Vous pouvez trouver la réponse à la main, mais vous pouvez aussi intégrer à fusion une variable globale nb_comp qui est incrémentée à chaque comparaison entre deux éléments de la liste.
Pensez à systématiquement réinitialiser nb_comp à 0 avant chaque appel de tri_fusion, car sinon la valeur continue à courir. C’est un des dangers de l’utilisation de variables globales dans les fonctions.

Tri par insertion

On va écrire une version itérative de l’algorithme de tri par insertion.

Son principe : on compare chacun des éléments i de la liste donnée en argument (à partir du deuxième) à ceux qui le précèdent en remontant la liste un par un (i-1,i-2,etc.). Tant qu’un des éléments qui précèdent est plus grand que l’élément i, on les permute, jusqu’à ce que l’élément i soit à la bonne place.

Construisez d’abord une fonction permute(L,i,j) qui permute les éléments i et j d’une liste L.

def permute(L,i,j):
    """
    permute(L: list,i: int,j: int) -> None
    préconditions: 0 < i,j < len(L)
    """
    ### VOTRE CODE

# Tester tous les cas particulier auxquels vous pensez qui pourraient mettre votre fonction en défaut
L = [1,2,3]
permute(L,0,2)
L

Puis complétez la fonction tri_insertion en utilisant permute.

def tri_insertion(L):
    """
    tri_insertion(L: list) -> None
    """
    for i in range(1,len(L)):
        j = i
        X = L[i]
        while j > 0 and L[j-1] > X:
            ### VOTRE CODE
            j -= 1

La cellule de tests suivante permet de comparer le résultat de la fonction tri_insertion à la fonction native de tri sort sur 1000 listes de 10 nombres tirés au hasard entre -5 et 5. Si pas d’AssertionError, a priori votre fonction… fonctionne.

from random import randint
for i in range(1000):
    L_desord = [randint(-5,5) for i in range(10)]
    L_desord_copie1 = L_desord[:] # attention à ne pas juste écrire L_desord_copie1 = L_desord (copie superficielle) !
    L_desord_copie2 = L_desord[:]
    L_desord_copie1.sort()
    tri_insertion(L_desord_copie2)
    assert L_desord_copie1==L_desord_copie2, f"y a un problème avec {L_desord} :\ndonne {L_desord_copie2}\nau lieu de {L_desord_copie1}"

Combien de comparaisons entre deux éléments de la liste effectue l’algorithme de tri insertion pour ordonner [1,2,3,4,5,6,7,8] et [8,7,6,5,4,3,2,1] ?

• A : 7 et 28
• B : 0 et 7
• C : 28 et 28
• D : 5 et 35

Combien de comparaisons entre deux éléments de la liste demande le tri par insertion d’une liste de 200 éléments rangés en ordre inverse ?

Tri par sélection

Principe : parmi les éléments de la liste, on cherche le plus petit, et on le permute avec le premier élément. Puis on recommence avec tous les éléments restants (tous moins le premier) : on cherche le plus petit et on le permute avec le deuxième élément. On recommence jusqu’à épuiser la liste

fonction tri_selection(liste L)
    n ← longueur(L)
    pour i de 0 à n - 2
        min ← i
        pour j de i + 1 à n - 1
            si L[j] < L[min], alors min ← j
        fin pour
        si min ≠ i, alors échanger L[i] et L[min]
    fin pour
fin fonction

Traduisez le pseudocode ci-dessus en python.

def tri_selection(L):
    ### VOTRE CODE

Combien de comparaisons entre deux éléments de la liste effectue l’algorithme de tri par sélection pour ordonner [1,2,3,4,5,6,7,8] et [8,7,6,5,4,3,2,1] ?

• A : 7 et 28
• B : 0 et 7
• C : 28 et 28
• D : 5 et 35

Le tri par sélection ressemble beaucoup au tri par insertion. Dans les deux, après k traversées de la liste, les k premiers éléments sont triés. Cependant la différence fondamentale entre les deux algorithmes est le sens dans lequel ces tris s’opèrent ; le tri par insertion trie de la fin vers le début alors que le tri par sélection trie du début vers la fin.
Conséquence : dans le tri par sélection, les k premiers éléments de la liste en cours de tri sont les plus petits de la liste entière alors que dans le tri par insertion, ce sont seulement les k premiers éléments d’origine qui sont triés.

Le tri par sélection doit toujours inspecter tous les éléments restant pour trouver le plus petit, tandis que le tri par insertion ne requiert qu’une seule comparaison quand le (k+1)^e élément est plus grand que le k^e ; lorsque c’est fréquent (si la liste est déjà partiellement triée), le tri par insertion est bien plus efficace. En moyenne, le tri par insertion nécessite de comparer et décaler la moitié des éléments seulement, ce qui correspond donc à la moitié des comparaisons que le tri par sélection doit faire.

Dans le pire des cas pour le tri par insertion (liste triée en sens inverse), les deux tris opèrent autant d’opérations l’un que l’autre, mais le tri par insertion va nécessiter plus de permutations puisqu’il décale toujours d’une position voisine à l’autre. Le dernier élément d’une liste renversée, par exemple, va devoir traverser toute la liste en échangeant sa place avec chacun des éléments qui le précèdent, alors qu’avec le tri par sélection, il n’y a jamais au plus qu’une permutation par élément.

En général, le tri par insertion va écrire dans la liste $O(n^2)$ fois (chaque permutation écrit dans la liste), alors que le tri par sélection va écrire seulement $O(n)$ fois. Pour cette raison, le tri par sélection peut être préférable au tri par insertion lorsque l’écriture sur la mémoire est significativement plus coûteuse que la lecture (comme sur les EEPROM ou sur les mémoires flash). Ce point est illustré dans l’animation interactive du début car limiter les permutations y correspond à limiter les déplacements, ce qui donne l’illusion d’un algorithme plus rapide.

Tri à bulles

Le tri à bulles est surtout à visée pédagogique, il ne sert quasiment jamais réellement. Il tire son nom du fait qu’on pousse vers la fin de la liste, de proche en proche, des éléments de plus en plus grands, comme une bulle qui grossit en remontant à la surface.

def tri_a_bulles(L):
    n = len(L)
    for i in range(n-1):
        for j in range(n-i-1):
            if L[j] > L[j+1]:
                permute(L,j,j+1)
    return L

Combien de comparaisons effectue l’algorithme de tri à bulles pour ordonner [1,2,3,4,5,6,7,8] et [8,7,6,5,4,3,2,1] ?

• A : 7 et 28
• B : 0 et 7
• C : 28 et 28
• D : 5 et 35

Combien de comparaisons demande le tri à bulles d’une liste de 200 éléments rangés en ordre inverse ?

Tri rapide

Le tri rapide n’est pas toujours le plus rapide… Mais il peut l’être (surtout sur les grandes listes) !
C’est un algorithme récursif utilisant une partition de la liste à trier.
Son avantage sur le tri fusion est d’être un tri en place.
Désavantage : il est instable.

from random import randint

def partition(L, g, d):
    p = L[g]
    i = g+1
    for j in range(g+1,d+1):
        if L[j] < p:
            permute(L,i,j)
            i += 1
    permute(L,g,i-1)
    return i-1

def tri_rapide_gd(L, g, d):
    if g < d: 
        pivot = randint(g,d)
        permute(L,pivot,g)
        pivot = partition(L, g, d)
        tri_rapide(L, g, pivot-1)
        tri_rapide(L, pivot+1, d)
    return L

Pour ne pas s’embêter avec g et d, on peut encapsuler tri_rapide_gd dans une nouvelle fonction dont le seul rôle est d’initialiser g et d.

def tri_rapide(L):
    g = 0
    d = len(L)-1
    tri_rapide_gd(L, g, d)

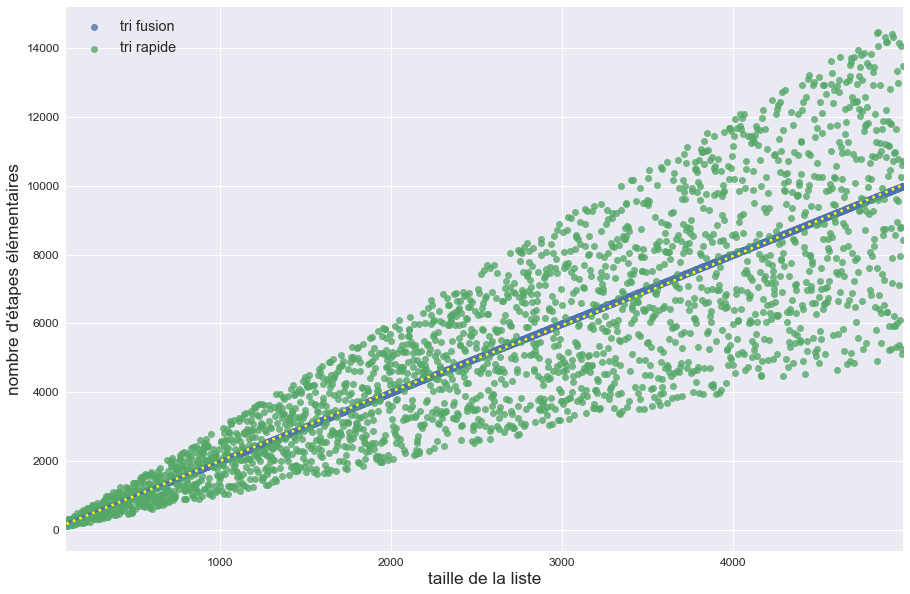
La figure précédente permet de supposer que la complexité dans le pire des cas du tri fusion est égale à sa complexité dans le meilleur des cas et à la complexité en moyenne du tri rapide.

Sur la vidéo qui suit, des danseurs hongrois exécutent une implémentation classique du tri rapide utilisant systématiquement le premier élément comme pivot (et non un élément tiré au hasard) et où la partition marche un peu différemment : le chapeau rouge (élément comparé au pivot) est donné au voisin le plus proche du pivot et quand le pivot récupère le chapeau rouge, il est à la bonne place.

En levant la contrainte d’un tri en place, on escamote lâchement la réelle difficulté et on peut maintenant s’affranchir de la fonction de partition, ce qui permet un code bien plus court et clair.
On va visualiser les différents appels récursifs d’un tel code grâce au module introduit dans le TP précédent.

from recursionvisualisation import viz, CallGraph
cg = CallGraph()
@viz(cg)

def triRapide(elements):
    if len(elements) <= 1:
        return elements
    else: 
        pivot = elements[0]
        plusPetit = triRapide([e for e in elements[1:] if e <= pivot])
        plusGrand = triRapide([e for e in elements[1:] if e > pivot])
        return plusPetit + [pivot] + plusGrand

print(triRapide("hanniballecter"))
cg.render()

['a', 'a', 'b', 'c', 'e', 'e', 'h', 'i', 'l', 'l', 'n', 'n', 'r', 't']

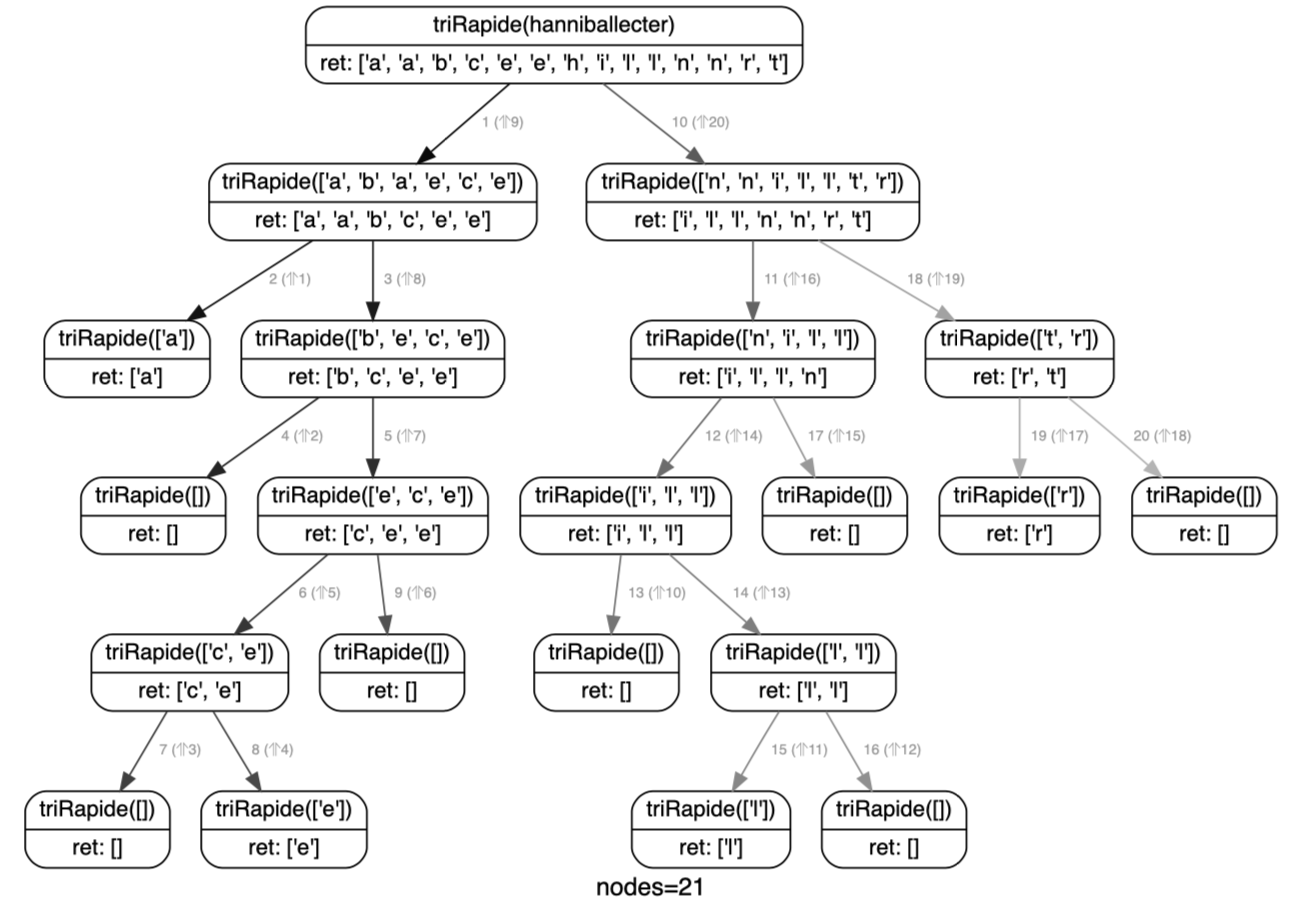
Placer le pivot en premier élément a un inconvénient : triRapide devient très lent avec les listes déjà triées (ou quasi triées).

Quelle sera la taille de la pile d’exécution si on donne en argument à triRapide une liste déjà triée de 500 éléments ?

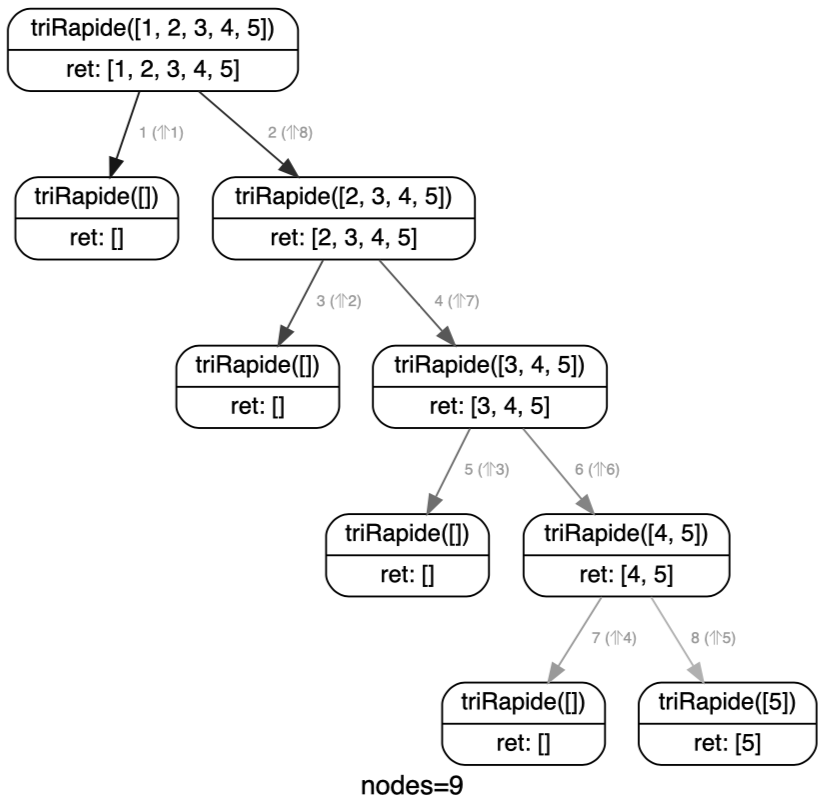
Les tris par comparaison n’ont que faire de la nature des éléments de la liste à trier du moment qu’on peut les comparer entre eux. On peut ainsi trier tout aussi bien des chaînes de caractères que des flottants.
Par contre, si les éléments de la liste sont contraints d’une façon ou d’une autre, on peut essayer de tirer parti de la situation.

Tris non comparatifs

Tri par dénombrement (ou par comptage)

Si la liste à trier n’est constituée que d’entiers positifs, on peut mettre au point un tri très rapide n’utilisant aucune comparaison : le tri par dénombrement (counting sort).

Principe : on construit un histogramme des valeurs de la liste à trier L dans une liste intermédiaire L_eff.

• Si m est la plus grande valeur des éléments de la liste à trier, alors la taille de L_eff doit valoir m+1. Et on initialise toutes ses valeurs à zéros. Chaque valeur L[i] de la liste à trier est donc aussi un indice de la liste L_eff !
• On parcourt ensuite la liste à trier et on incrémente de 1 la valeur de l’élément L_eff[L[i]] de la liste intermédiaire. On obtient bien ainsi les effectifs pour chaque valeur de la liste à trier.
• Il suffit enfin de parcourir L_eff depuis le début et pour chaque élément L_eff[i] non nul, d’ajouter à une nouvelle liste L_sortie autant de fois i que la valeur de L[i].
• Plus qu’à retourner L_sortie.

Implémentez la fonction tri_par_denombrement telle qu’elle est décrite ci-dessus.

def tri_par_denombrement(L,m):
    """
    tri_par_denombrement(L: list,m: int) -> L_sortie: list
    m est la valeur maximum des éléments de L 
    """
    ### VOTRE CODE

Le nombre d’étapes de tri_denombrement peut s’écrire en fonction du nombre d’éléments n de la liste comme (on considérera que m est une constante) :

• A : $a$
• B : $a\times n + b$
• C : $a\times n^2+b\times n + c$
• D : $a\times n^3+b\times n^2 + c\times n + d$

Comparer les tris

Essayons maintenant de classer ces tris suivant différents critères.
Commençons par ce qui est souvent le plus critique : leur complexité en temps. À quoi doit-on s’attendre lorsque la taille de la liste à trier prend un facteur d’échelle ?

Complexité en temps

Le graphe suivant présente le temps mis par les différents algorithmes pour trier des listes de taille croissante.

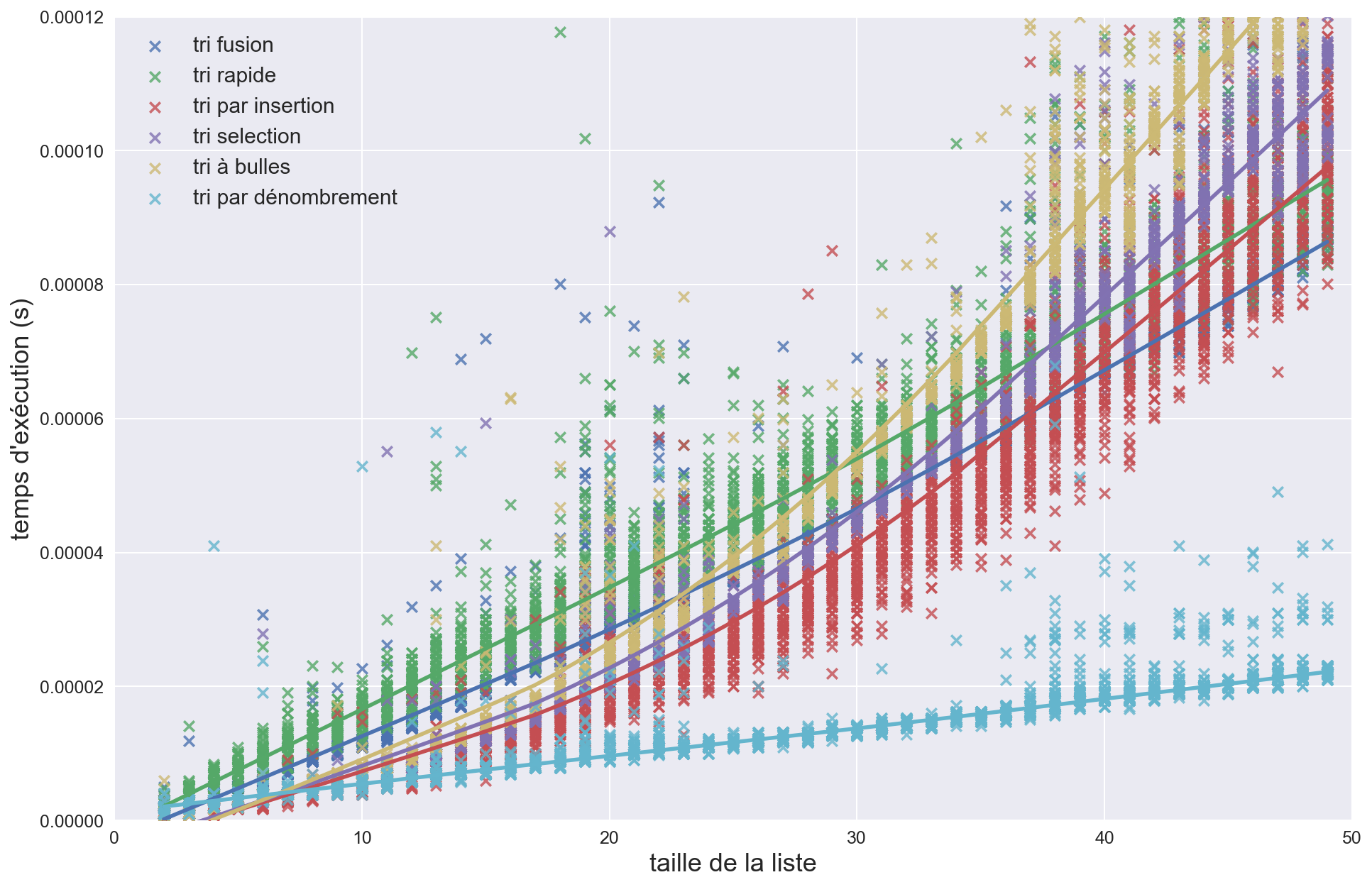
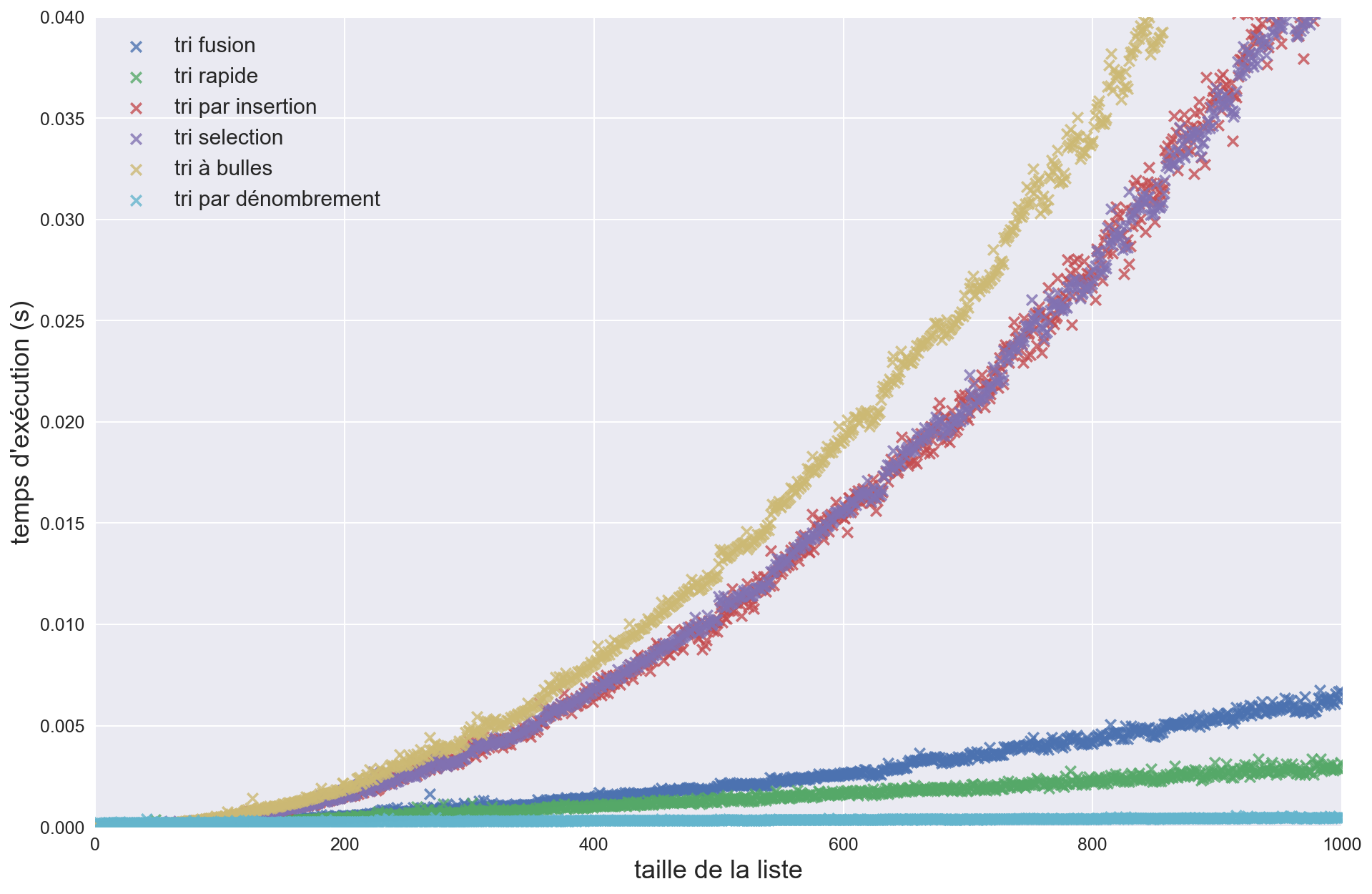
On peut classer ces algorithmes en 3 catégories de complexité temporelle :

• les tris par insertion, sélection et à bulles sont de complexité quadratique ($O(n^2)$)
• les tris fusion et rapide sont quasilinéaires ($O(n\log n)$)
• le tri par dénombrement est linéaire ($O(n)$)

Pour des petites listes (et lorsque des tris non comparatifs ne sont pas applicables), le tri par insertion est en moyenne plus rapide que les autres alors que pour des grandes listes, c’est le tri rapide qui domine.

Complexité en espace : en place ou non ?

L’algorithme a-t-il besoin d’utiliser une liste intermédiaire pour opérer son tri ou parvient-il à écrire directement sur la liste d’origine ? Dans ce dernier cas, les tri est dit en place.

Dans la liste suivante, affectez à chaque variable correspondant à un algorithme de tri le caractère 'O' si son tri se fait en place ou 'X' sinon.

# Retirer la mauvaise réponse
triinsertion    = 'O' 'X'
tiselection     = 'O' 'X'
triabulles      = 'O' 'X'
trifusion       = 'O' 'X'
trirapide       = 'O' 'X'
tridenombrement = 'O' 'X'

Stabilité

Un algorithme de tri est stable s’il conserve l’ordre relatif de départ entre deux valeurs égales.
Dans l’animation suivante, un algorithme est stable si les deux barres noires et blanches restent toujours dans le même ordre après et avant le tri.

On compte le nombre de fois que les caractères ‘r’, ‘c’, ‘q’ et ‘p’ apparaissent dans cette phrase :

• ‘r’ : 6
• ‘c’ : 5
• ‘q’ : 2
• ‘p’ : 5

On crée à partir de ces données le tuple (('r',6),('c',5),('q',2),('p',5)).
Si on trie ce tuple selon le premier élément de chacune des paires qu’il contient (tri alphabétique), tous les tris donnent le même résultat :
(('c',5),('p',5),('q',2),('r',6))
Mais si maintenant, on part de ce tuple trié et qu’on le trie en fonction des effectifs, les algorithmes ne sont pas tous d’accords !

Pour vous en convaincre triez à la main (('c',5),('p',5),('q',2),('r',6)) selon le deuxième élément de chacun des tuples en suivant l’algorithme du tri à bulle, puis en suivant l’algorithme de tri insertion.
Notez ci-dessous les tuples obtenus.

# tuple obtenu avec le tri à bulle (modifiez le tuple pour qu'il corresponde à ce que vous avez trouvé)
T1 = (('c',5),('p',5),('q',2),('r',6))
# tuple obtenu avec le tri insertion (modifiez le tuple pour qu'il corresponde à ce que vous avez trouvé)
T2 = (('c',5),('p',5),('q',2),('r',6))

On dit alors que le tri insertion n’est pas stable car il ne conserve pas nécessairement l’ordre de deux éléments égaux.

• tris instables : le tri sélection et le tri rapide.
  
• tris stables : le tri insertion, le tri à bulle et le tri fusion

Un tri instable peut sans trop de peine être rendu stable, il suffit de garder la trace de l’ordre initial pour les éléments égaux, mais cela a un coût !
L’instabilité du tri par sélection peut être éliminée en utilisant une fonction intermédiaire minimum cherchant l’indice du plus petit des éléments restant à trier et en ajoutant successivement les éléments trouvés dans une nouvelle liste tout en les retirant de la première liste (on détricote la liste de départ pour retricoter à l’endroit la liste triée). Mais l’algorithme n’est alors plus en place ! On a troqué l’instabilité contre de la place mémoire.

Donnez le code de minimum et tri_selection_stable (avec une contrainte supplémentaire : le bloc de code de tri_selection_stable ne devra pas dépasser 4 lignes). Pour retirer un élément d’une liste, vous pouvez regarder ici.

def minimum(L):
    """
    minimum(L: list) -> imin: int
    imin est l'indice du plus petit élément de la liste
    et s'il y a plusieurs minimaux, imin est le plus petit des indices
    """
    ### VOTRE CODE

# le bloc de code de tri_selection_stable ne devra pas dépasser 4 lignes pour être considéré comme juste.
    
def tri_selection_stable(L) :
    ### VOTRE CODE