Complexité d’un algorithme
Parmi les 3 questions qu’on peut se poser naturellement devant un algorithme (termine-t-il ? est-il correct ? combien de temps met-il ?), on a laissé la dernière en plan dans le chapitre précédent.
La question du temps mis par l’algorithme est le problème de la complexité de l’algorithme.
L’objectif premier d’un calcul de complexité algorithmique est de pouvoir comparer l’efficacité d’algorithmes résolvant le même problème. Dans une situation donnée, cela permet donc d’établir lequel des algorithmes disponibles est le meilleur (du point de vue temps d’exécution).
complexité en temps
Réaliser un calcul de complexité en temps revient à décompter le nombre d’opérations élémentaires (affectation, calcul arithmétique ou logique, comparaison…) effectuées par l’algorithme.
Pour rendre ce calcul réalisable, on émettra l’hypothèse que toutes les opérations élémentaires sont à égalité de coût. En pratique ce n’est pas tout à fait exact, mais cette approximation est cependant raisonnable.
On pourra donc estimer que le temps d’exécution de l’algorithme est proportionnel au nombre d’opérations élémentaires.
La complexité $T(n)$ d’un algorithme va naturellement être fonction de la taille $n$ des données passées en entrée. Cette dépendance est logique, plus ces données seront volumineuses, plus il faudra d’opérations élémentaires pour les traiter.
Souvent la complexité dépendra aussi de la donnée en elle même et pas seulement de sa taille. En particulier la façon dont sont réparties les différentes valeurs qui la constituent.
Rappelons-nous par exemple l’algorithme de recherche séquentielle d’un élément dans une liste non triée du cours “structures de données”. Le principe de l’algorithme est simple, on parcourt un par un les éléments jusqu’à trouver, ou pas, celui recherché. Ce parcours peut s’arrêter dès le début si le premier élément est “le bon”. Mais on peut également être amené à parcourir la liste entière si l’élément cherché est en dernière position, ou même n’y figure pas. Le nombre d’opérations élémentaires effectuées dépend donc non seulement de la taille de la liste, mais également de la répartition de ses valeurs.
Cette remarque nous conduit à préciser un peu notre définition de la complexité en temps. En toute rigueur, on devra en effet distinguer trois formes de complexité en temps :
- la complexité dans le meilleur des cas : c’est la situation la plus favorable, qui correspond par exemple à la recherche d’un élément situé à la première postion d’une liste, ou encore au tri d’une liste déjà triée.
- la complexité dans le pire des cas : c’est la situation la plus défavorable, qui correspond par exemple à la recherche d’un élément dans une liste alors qu’il n’y figure pas, ou encore au tri par ordre croissant d’une liste triée par ordre décroissant.
- la complexité en moyenne : on suppose là que les données sont réparties selon une certaine loi de probabilités.
On calcule le plus souvent la complexité dans le pire des cas, car elle apporte une garantie (pas de mauvaises surprises en tablant sur le pire).
Dernière chose importante à prendre en considération, si la donnée est un nombre entier, la façon de le représenter influera beaucoup sur l’appréciation de la complexité.
Par exemple, si $n=2020$, on peut considérer que la taille de $n$ est :
soit la valeur de $n$ en elle-même, façon la plus naturelle de voir les choses, c.-à-d. $2020$,
soit le nombre de chiffres que comporte l’écriture en binaire de $n$, c.-à-d. 11,
soit le nombre de chiffres que comporte l’écriture en décimal de $n$, c.-à-d. 4.
Vu la finalité informatique de nos algorithmes, nous devrions choisir le nombre de chiffres dans l’écriture binaire de l’entier, mais par souci de simplicité, on considèrera le plus souvent la valeur de l’entier comme taille.
Néanmoins, lors de l’étude de la complexité des algorithmes arithmétiques (test de primalité, algorithme d’Euclide, etc.), la taille de l’entier est le paramètre important et il faudra donc considérer la taille de l’entrée $n$ comme étant $\log_2(n)$.
Exemple : la fonction somme
1def somme(L):
2 s = 0
3 for e in L:
4 s += e
5 return s
Le calcul
somme([1,2,3])nécessite à priori 4 opérations (1 fois la ligne 2, et 3 fois la ligne 4). Toutefois, la notion d’opération élémentaire n’est pas précisément définie : on pourrait considérer par exemple que la ligne 4 fait non pas une, mais deux opérations élémentaires (une somme puis une affectation) et alorssomme([1,2,3])nécessiterait 7 opérations.
Cette imprécision est sans conséquence, car on estime la complexité “à la louche”. Pour définir formellement ce que signifie ce “à la louche”, nous introduisons les trois notations suivantes :
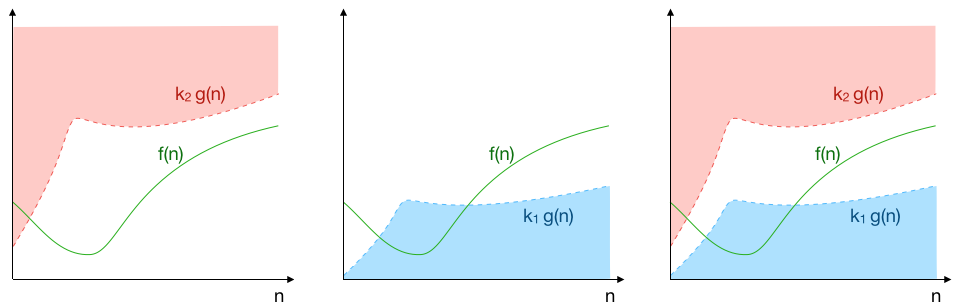
Étant donné deux fonctions $\mathbb{N}\rightarrow \mathbb{R}^*_+$ $f$ et $g$ :
$f(n)$ est un grand $\mathcal{O}$ de $g(n)$ s’il existe une constante $k_2$ telle que pour tout $n$ assez grand $f(n)≤k_2\cdot g(n)$ ;
on note $f(n) = \mathcal{O}(g(n))$.
Et on dit que $g$ domine $f$ asymptotiquement.
$f(n)$ est un grand $\Omega$ de $g(n)$ s’il existe une constante $k_1>0$ telle que pour tout $n$ assez grand $k_1\cdot g(n)≤f(n)$ ;
on note $f(n) = \Omega(g(n))$.
$f(n)$ est un grand $\Theta$ de $g(n)$ s’il existe deux constantes $k_1>0$ et $k_2$ telles que pour tout $n$ assez grand $k_1\cdot g(n)≤f(n)≤k_2\cdot g(n)$ ;
on note $f(n) = \Theta(g(n))$.
$f$ et $g$ sont asymptotiquement du même ordre de grandeur.
Comme on l’a dit, notre souhait est de connaître le nombre d’étapes que nécessitera l’algorithme dans le pire des cas, quitte à le surestimer. On veut par contre absolument éviter de le sous-estimer ; on se concentre alors sur la première notation, grand $O$ (correspondant à la majoration).
En effet, si on sait que $T(n)=O(g(n))$, on est alors assuré que le nombre d’étapes $T(n)$ ne sera asymptotiquement jamais plus grand que $g(n)$ (asymptotiquement signifiant en pratique “pour des $n$ suffisamment grands”).
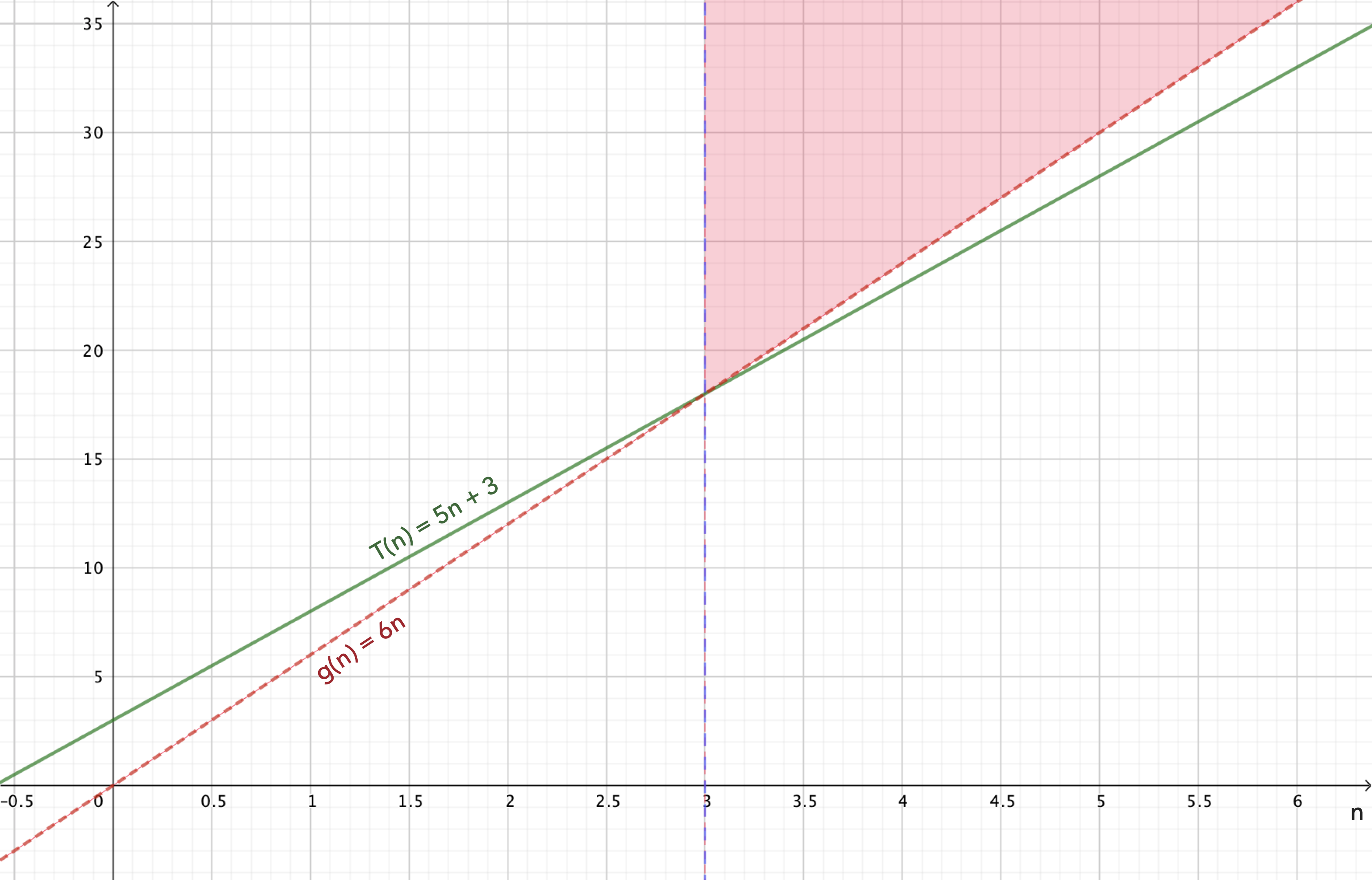
Exemple : $T(n)=5n+3$
Dès $n>3$, $T(n)<6n$, ce qu’on réécrit $T(n)<6\times g(n)$ avec $g(n)=n$, d’où’ $T(n)=O(n)$.
Les complexités algorithmiques sont exprimées comme des grands $\mathcal{O}$ ou grands $\mathcal{\Theta}$ des fonctions de référence. Cela va nous permettre de les classer.
Des algorithmes appartenant à une même classe sont alors considérés comme de complexité équivalente ; ils ont la même efficacité.
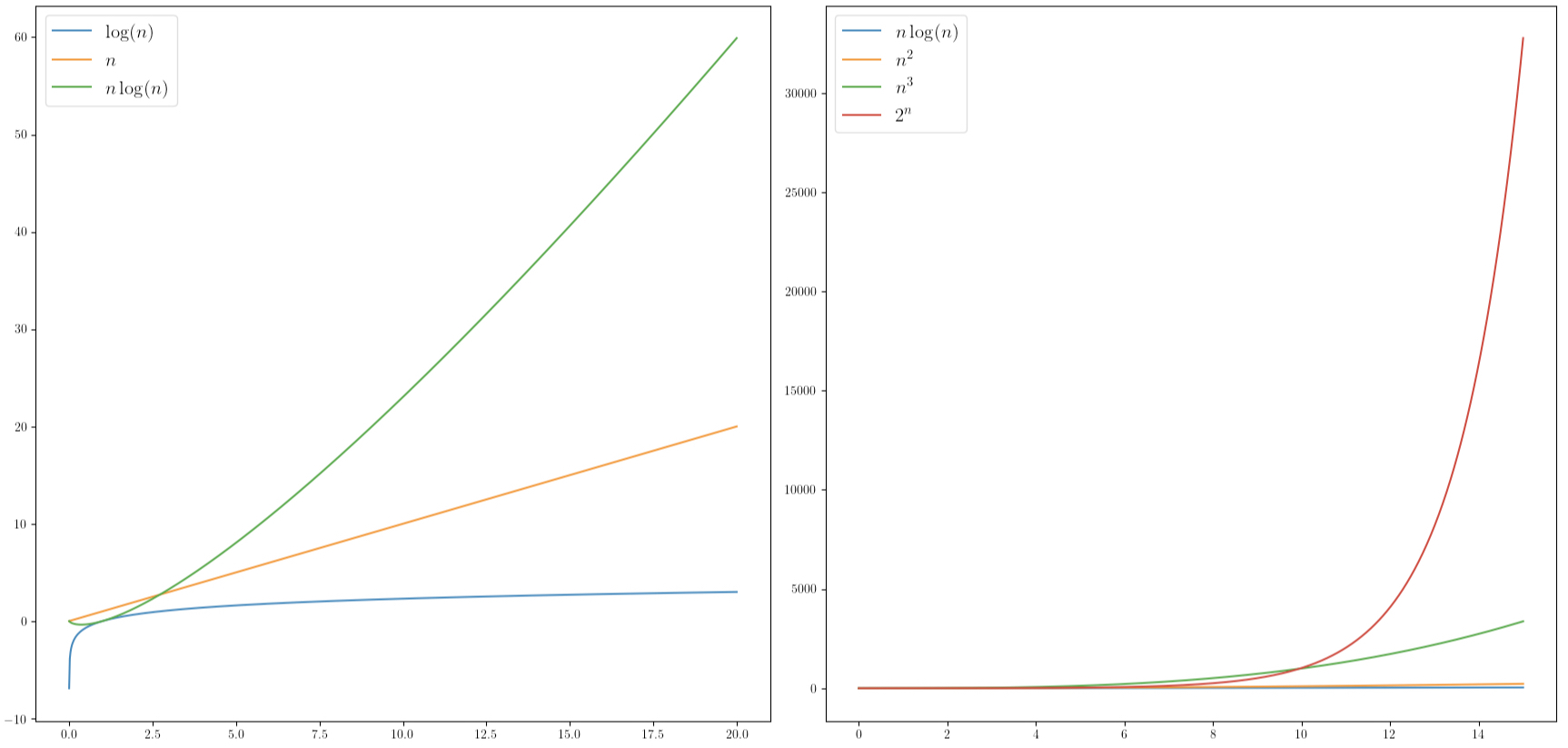
Le tableau suivant récapitule les complexités de référence (rangées par ordre croissant) :
| $\mathcal{O}$ | Type de complexité |
|---|---|
| $\mathcal{O(1)}$ | constant |
| $\mathcal{O}(\ln(n))$ | logarithmique |
| $\mathcal{O}(n)$ | linéaire |
| $\mathcal{O}(n\times\ln(n))$ | quasi-linéaire |
| $\mathcal{O}(n^2)$ | quadratique |
| $\mathcal{O}(n^3)$ | cubique |
| $\mathcal{O}(2^n)$ | exponentiel |
| $\mathcal{O}(n!)$ | factoriel |
Lors de la somme de deux complexités de types différents, la classe de plus grande complexité domine.
Par exemple : $\mathcal{O}(n)+\mathcal{O}(n^2)=\mathcal{O}(n^2)$.
Si $T(n)$ est un grand $O$ d’une certaine fonction $g$, alors il sera un grand $O$ de toutes les fonctions $h$ qui dominent $g$ (toutes les fonctions appartenant à une classe de complexité supérieure). Laquelle de ces classes désigne la complexité de $T(n)$ ?
On choisit toujours la plus petite classe possible pour définir la classe de complexité de $T(n)$, car si on cherche bien à se prémunir contre les mauvaises surprises, cela ne sert à rien de s’assurer contre l’impossible (cela reviendrait à toujours répondre l’infini quand on nous demande une borne supérieure, c’est certes vrai mais pas très utile…).
Moralité, quand on parle de grand $O$, la plupart du temps, il s’agit en fait de grand $Θ$.
Dans l’exemple de $5n+3$, on a $T(n) = O(n)$, et par conséquent on a aussi $T(n)=O(n^2)$, $T(n)=O(n^3)$, etc.
Mais attention, quand on nous demande la complexité asymptotique au pire de $T(n)$, la réponse attendue est bien $O(n)$ !
Ordres de grandeurs : en supposant qu’un système donné permette un milliard d’opérations par seconde (de type constant), on obtient les valeurs de temps d’exécution suivantes en fonction du type de complexité et de la taille des données :
| taille des données | $\ln n$ | $n$ | $n\ln n$ | $n^2$ | $n^3$ | $2^n$ | $n!$ |
|---|---|---|---|---|---|---|---|
| $10^2$ | $5$ ns | $100$ ns | $500$ ns | $10$ μs | $1$ ms | $4.10^{13}$ ans | $3.10^{141}$ ans |
| $10^3$ | $7$ ns | $1$ μs | $7$ μs | $1$ ms | $1$ s | ||
| $10^4$ | $9$ ns | $10$ μs | $90$ μs | $100$ ms | $17$ min | ||
| $10^5$ | $12$ ns | $100$ μs | $1,2$ ms | $10$ s | $12$ jours | ||
| $10^6$ | $14$ ns | $1$ ms | $14$ ms | $17$ min | $32$ ans |
Quelques relations utiles (valables pour toute constante $c$) :
(1) $\mathcal{O}(n+c)=\mathcal{O}(n)$
(2) $\mathcal{O}(cn)=\mathcal{O}(n)$
(3) $\mathcal{O}(n/c)=\mathcal{O}(n)$
(4) $\mathcal{O}(c)=1$
(5) $n\times\mathcal{O}(1)=\mathcal{O}(n)$
Exemples :
- Le calcul de la somme des $n$ premiers entiers à l’aide d’une formule explicite (
n*(n+1)//2) est de complexité constante. - Ce même calcul réalisé de façon itérative grâce à la fonction
somme()est de complexité linéaire. En effet, la taille de l’entrée est $n=$len(L)et la complexité est en : $$T(n)=\underbrace{\mathcal{O}(1)}_\text{ligne 2}+\underbrace{n\times \underbrace{\mathcal{O}(1)}_\text{ligne 4}}_{\text{for}}=\mathcal{O}(n)$$ - L’algorithme de recherche par dichotomie (TP4) est de complexité logarithmique puisque l’algorithme nécessite au pire $\log_2 n$ passages dans la boucle et chaque instruction dans la boucle (comparaison, division euclidienne, affectations) se fait en temps constant $$T(n)=\log_2(n)\times \mathcal{O}(1) = \mathcal{O}(\ln n)$$
Plus tordu : trouvons la complexité de la fonction neufs() suivante qui calcule naïvement le plus grand nombre de 9 consécutifs dans l’écriture en base 10 de $n$.
def neufs(n):
L = []
while n!= 0:
L.append(n%10)
n //= 10
M = 0
for k in range(len(L)):
i = k
while i < len(L) and L[i]==9:
i += 1
M = max(M, i - k)
return M
Chacune des instructions utilisées est en $\mathcal{O}(1)$ (temps constant). On utilise bien
maxqui a une complexité linéaire, mais on ne l’utilise que sur 2 valeurs.
On passe dans le premierwhileune fois par chiffre de $n$ en base 10 (n//10fait perdre un chiffre à $n$), soit environ $\log_{10}(n)$ fois.
La listeLcontient alors (à moins de 1 près) $\log_{10}(n)$ valeurs. On passe dans lefor$\log_{10}(n)$ fois, et au pire le même nombre de fois dans le secondwhile.
La complexité est donc $T(n)=\underbrace{\log_{10}(n) \times \mathcal{O}(1)}{\text{premier while}}+\underbrace{\log{10}(n) \times\log_{10}(n) \times\mathcal{O}(1)}_{\text{boucles imbriquées}}=\mathcal{O}(\ln ^2 n)$
La complexité sert essentiellement à comparer les algorithmes.
On peut aussi tenter de confirmer expérimentalement nos conclusions en mesurant le temps mis par la machine pour faire tourner l’algorithme. Grâce au module time, on va ainsi pouvoir vérifier empiriquement que l’algorithme de recherche par dichotomie est bien meilleur que l’algorithme de recherche naïf. On va aussi tenter d’en savoir plus sur l’opérateur natif in qui accomplit la même fonction.
Pour cela, on va mesurer le temps mis par les différentes méthodes pour chercher un nombre au hasard entre $0$ et $b$ dans une liste des $b$ premiers entiers. On moyenne ce temps en faisant $50\,000$ essais avec des nombres à rechercher différents. Puis on multiplie $b$ par $2$ et on recommence :
import random
import time
b, m = 1, 50000
print('\n| n | tps algo naïf | tps algo dicho | tps "in" |')
print('-'*54)
for i in range(12):
b *= 2
T = [i for i in range(0,b)]
t1 = t2 = t3 = 0
for j in range(m):
x = random.randint(0,b)
d1 = time.time() #time() note la valeur de l'horloge (en s)
recherche_naïve(x,T)
f1 = time.time()
d2 = time.time()
recherche_dicho(x,T)
f2 = time.time()
d3 = time.time()
x in T
f3 = time.time()
t1 += f1 - d1 #f1-d1 = laps de temps qu'a duré la recherche linéaire
t2 += f2 - d2 #f2-d2 = laps de temps qu'a duré la recherche dicho
t3 += f3 - d3 #f3-d3 = laps de temps qu'a duré la recherche avec "in"
print('| {:>4d} |{:^15.2E}|{:^16.2E}|{:^12.2E}|'.format(b,t1/m,t2/m,t3/m))
------------------------------------------------------
| 2 | 3.56E-07 | 6.81E-07 | 1.90E-07 |
| 4 | 4.04E-07 | 7.87E-07 | 2.12E-07 |
| 8 | 4.58E-07 | 8.58E-07 | 2.38E-07 |
| 16 | 5.86E-07 | 9.48E-07 | 2.80E-07 |
| 32 | 8.11E-07 | 1.06E-06 | 3.60E-07 |
| 64 | 1.30E-06 | 1.19E-06 | 5.37E-07 |
| 128 | 2.25E-06 | 1.33E-06 | 8.83E-07 |
| 256 | 4.18E-06 | 1.53E-06 | 1.57E-06 |
| 512 | 8.09E-06 | 1.87E-06 | 2.96E-06 |
| 1024 | 1.57E-05 | 2.14E-06 | 5.70E-06 |
| 2048 | 3.09E-05 | 2.38E-06 | 1.12E-05 |
| 4096 | 6.13E-05 | 2.63E-06 | 2.22E-05 |
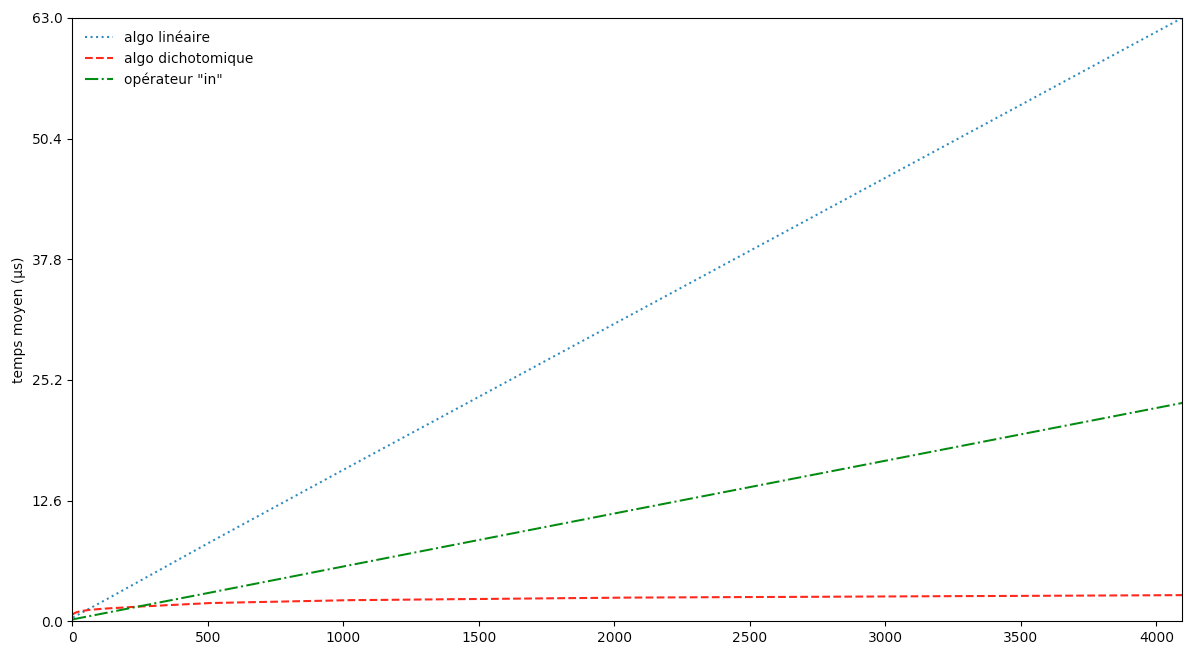
in est plus rapide que l’algo de recherche naïf mais ils réagissent tous deux pareil à un changement d’échelle ; si on on multiplie n par 2, les deux algorithmes mettent 2 fois plus de temps. C’est ce qui nous montre qu’ils ont la même complexité !
Pour la recherche dichotomique en revanche, une multiplication du nombre de valeur par 2 ne se solde pas par un doublement du temps, mais par l’ajout d’un temps constant seulement. C’est typique d’une complexité logarithmique.
On remarque que
L’opérateur in semble de complexité linéaire. Derrière ces deux petits caractères se cache donc du code loin d’être de la complexité constante des opérations de base. Ce n’est pas la taille qui compte…
Complexité en espace
La complexité en espace est quant à elle la taille de la mémoire nécessaire pour stocker les différentes structures de données utilisées lors de l’exécution de l’algorithme.
On considère pour simplifier qu’un type de base (un entier, un flottant, un caractère,…) occupe une place en mémoire constante (complexité en $\mathcal{O}(1)$).
Exemples :
Pour la fonction somme(), on constate que si la liste L contient des entiers ou des flottants, chaque variable intermédiaire (e et s) contient un type de base, donc demande une place en mémoire en $\mathcal{O}(1)$ et donc la complexité en mémoire au pire est en $\mathcal{O}(1)$.
Pour la fonction neufs(), la complexité en mémoire vient de la variable L (toutes les autres variables demandent $\mathcal{O}(1)$ en mémoire). Or cette variable va contenir environ $\log_{10}(n)$ éléments d’où une complexité en mémoire de $\mathcal{O}(\log_{10}(n)) = \mathcal{O}(\ln(n))$.
Retour sur les TP du premier semestre :
- TP 1 : quelle est la complexité des fonctions
recherche,recherche_dico,max,maximumetmax_2? - TP 2 : quelle est la complexité de
cherche_mot,cherche_duplicataetcherche_duplicata_bis? - TP 4 : quelle est la complexité de
recherche_dicho_corr? Et celle deracineen fonction du nombre de chiffres significatifs ? - TP 6 : trier les algorithmes de tri en différentes catégories de complexité.
Dans la vidéo suivante, on compare plusieurs algorithmes dont la mission est de trouver un doublon dans une liste. Quel est le meilleur ? Étudions leurs complexités en temps et en espace.