Graphes

Les graphes

Quelques points et des traits pour les relier suffisent pour créer un graphe. Cette grande simplicité est pourtant à l’origine d’un foisonnement mathématiques impressionnant.

Un peu d’histoire

L’acte de naissance de la théorie des graphes date d’une petite énigme à laquelle s’attelaient sans succès les habitants de Königsberg. Comment un voyageur pouvait traverser les sept ponts sans jamais passer deux fois sur le même pont ? Euler résout le problème et fonda du même coup la théorie des graphes !

Un graphe permet d’extraire l’essence du problème : les arêtes sont les ponts et les sommets (ou nœuds) sont les zones accessibles depuis ces ponts (séparées par les bras de rivière).

La forme précise des lignes reliant les points n’a pas d’importance : elles ne font qu’indiquer l’existance de laison entre ces points (cela illustre le caractère topologique et non géométrique du problème).

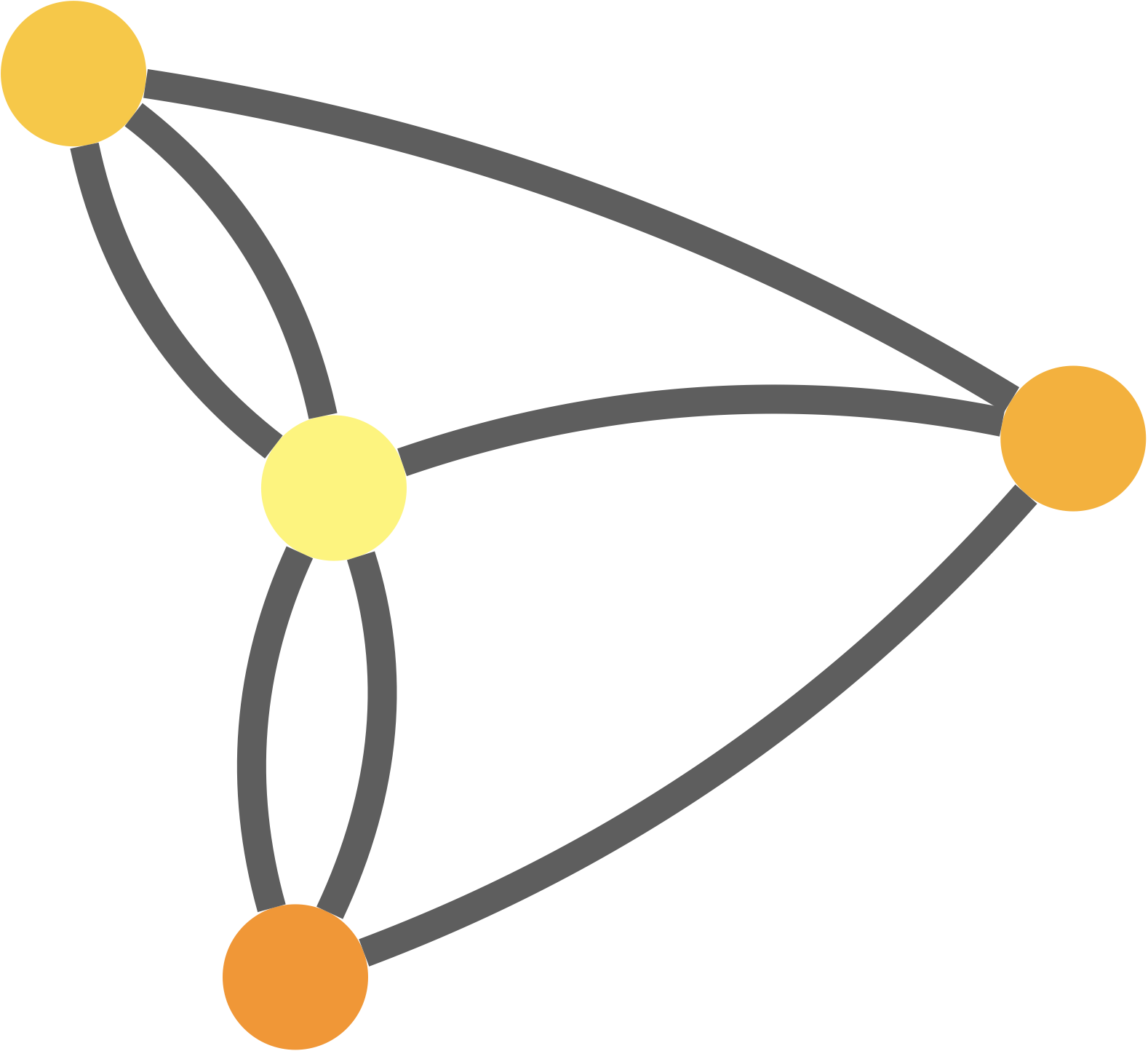
Euler compris alors que ce qu’on appelerait ensuite un chemin eulérien (un chemin reliant chaque sommet en ne passant qu’une fois par chaque arête) n’est possible que si le graphe ne compte pas plus de deux sommets d’où partent un nombre impair d’arêtes. Or dans le cas de Königsberg, il part un nombre impair d’arêtes de chacun des sept sommets ! Un chemin eulérien y est donc impossible.

Lorsqu’on trace un chemin eulérien sur un graphe, trois types de sommets se présentent : un sommet peut être soit un point de départ, soit un point d’arrivée, soit un point traversé (on y arrive puis on en repart). Et pour ces derniers, on aura toujours un nombre pair d’arêtes (autant d’arrivées que de départs)…

Ce premier pas d’Euler eut lieu en 1737, il fallut attendre ensuite plus de cent ans pour que Kirchhoff réutilise des graphes pour déterminer les intensités circulant dans les différentes branches d’un circuit électrique ; il met alors au point la notion d’arbre, des graphes sans boucle, en 1847.

Dix ans plus tard, c’est au tour de la chimie de s’attaquer aux graphes. En 1857, Cayley s’intéresse aux différentes structures possibles (isomères) d’une molécule ayant $n$ atomes de carbone et $2n+2$ atomes d’hydrogène (un alcane). Cela revient à trouver tous les arbres à $3n+2$ éléments tels que de chaque élément (chaque sommet) partent exactement une ou quatre arêtes (symbolisant les liaisons chimiques).

En 1869, enfin, les mathématiciens redécouvrent les graphes, par la voix de Jordan qui, sans connaître les travaux de Cayley, retrouve ses résultats.

Les jeux ne sont pas en reste : en 1859, le mathématicien et physicien irlandais William Hamilton invente “The Icosian Game”, dont le but est de visiter une et une seule fois tous les sommets d’un dodécaèdre régulier. Un tel chemin est depuis appelé hamiltonien.
Apparemment voisin du problème du chemin eulérien (visiter une et une seule fois chaque arête), le problème du chemin hamiltonien est en réalité beaucoup plus difficile.
Pour ce qui est du jeu que vous pouvez tester ci-dessous, une règle supplémentaire impose que la fin du chemin soit adjacente à son début. En rejoignant le point de départ, on formerait alors un cycle et on appelle ainsi cycle hamiltonnien un cycle passant par tous les sommets (pour pimenter les choses, un premier joueur choisit 5 sommets voisins les uns des autres et le deuxième joueur doit alors trouver les 15 restants ; c’est ça le jeu original d’Hamilton¹ , et il a prouvé que la victoire est alors toujours possible pour le deuxième joueur).

Le deuxième moitié du 20^e siècle et l’avènement de l’informatique voit la théorie des graphes prendre son véritable essor : c’est en effet l’outil idéal pour décrire les réseaux complexes modernes.

Les réseaux sont partout : les réseaux sociaux et les réseaux de communication, mais on trouve aussi des réseaux dans des champs scientifiques très différents comme en biologie, logistique, linguistique, économie, etc.

La théorie des graphes donne un langage commun à la description de ces réseaux.

Vocabulaire

Graphes non orientés

Un graphe $G$ est un ensemble de sommets (ou nœuds) S (notés $s_i$) et d’arêtes A (notées $\{s_i,s_j\}$) reliant deux à deux ces sommets. On note un tel graphe : $G = (S,A)$.

Quelques exemples dans des champs variés :

Réseau	Sommets	Arêtes
transport aérien	aéroports	vols
plans routiers	carrefours	tronçons de routes
réseau génétique	gènes	facteurs de transcription
cerveau	neurones	synapses
colonie de fourmis	jonctions	traces de phéromones
appels téléphoniques	numéro	appel
réseau de citation	auteur	citation

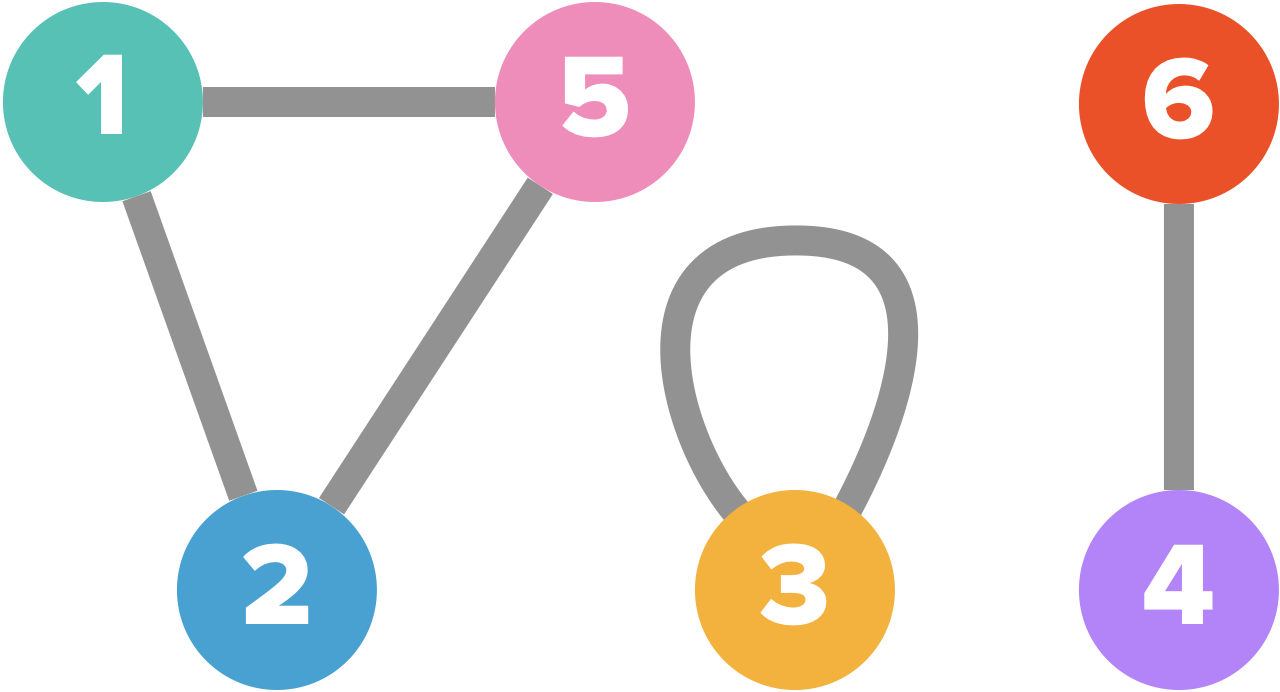Est représenté ci-dessus le graphe $G=(S,A)$ avec $S=\{1,2,3,4,5,6\}$ et $A=\{\{1,2\},\{1,5\},\{2,5\},\{3,3\},\{4,6\}\}$

Une boucle est une arête reliant un sommet à lui-même.

Exemple : il y a une boucle sur le sommet $3$.

L’ensemble des sommets adjacents (joints par une arête) au sommet $s_i$, autrement dit les voisins du sommet $s_i$, se note : $Adj(s_i)=\{s_j \in S,\{ s_i,s_j \}\in A\}$.

Exemple : $Adj(2)=\{1,5\}$

Un graphe non orienté est dit simple s’il ne comporte pas de boucle et jamais plus d’une arête entre deux sommets.

Le graphe ci-dessus n’est donc pas simple.

On appelle ordre d’un graphe le nombre de ses sommets ($card(S)$ ou plus simplement $|S|$).

Exemple : pour le graphe ci-dessus $|S|=6$

On appelle taille d’un graphe le nombre de ses arêtes ($card(A)$ ou $|A|$).

Exemple : pour le graphe ci-dessus $|A|=5$

Graphes orientés

Les arêtes d’un graphe non orienté sont symétriques, elles se parcourent indifféremment dans les deux sens, mais ce n’est pas toujours très pertinent. Considérons les exemples suivants :

Supposons que l’on veuille modéliser un plan routier. On associe naturellement un carrefour à un sommet et une rue à une arête. Mais on a besoin en plus d’une notion de direction pour représenter les rues à sens unique.
Pour modéliser des relations sociales, une arête entre Alice et Bob modélise un lien, mais comment représenter le fait que Bob connaisse Alice, mais que l’inverse soit faux ?
Dans un réseau d’ordinateur, en particulier sans fil, le lien entre deux nœuds est généralement non symétrique dans le sens où un message peut être envoyé de A vers B, mais pas l’inverse.

Pour modéliser ce type de situation, on utilise des graphes orientés.

Dans un graphe orienté, les sommets sont reliés par des arcs que l’on peut identifier à des couples de sommets (un couple a un ordre) : au couple $(a,b)$ correspond un arc d’origine $a$ et d’extrémité $b$.

L’arc $a = (s_i,s_j)$ est dit sortant en $s_i$ et incident ou entrant en $s_j$, et $s_j$ est un successeur de $s_i$, tandis que $s_i$ est un prédécesseur de $s_j$.

L’ensemble des successeurs d’un sommet $s_i \in S$ est noté $Succ(s_i) = \{s_j \in S,(s_i,s_j) \in A\}$.
L’ensemble des prédécesseurs d’un sommet $s_i \in S$ est noté $Pred(s_i) = \{s_j \in S,(s_j,s_i) \in A\}$.

Un graphe orienté permet, par exemple, de résumer les relations dans un chi-fou-mi (ici dans la variante puits montrant bien que jouer “pierre” est sans intérêt, ou encore dans la variante pierre-feuille-ciseaux-lézard-spock de The Big Bang Theory).

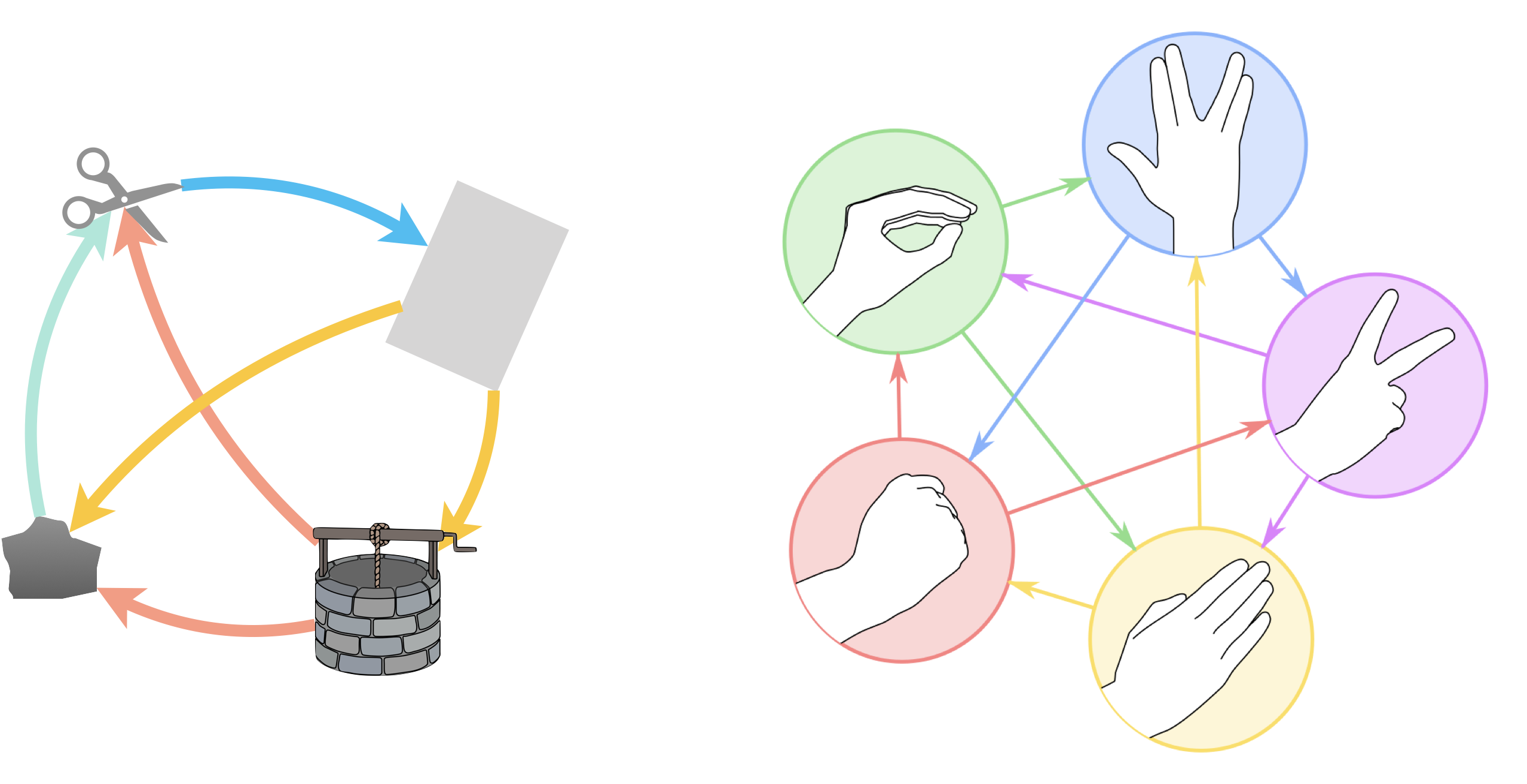
Pour “pierre-feuille-ciseaux-puits”, le graphe $G(S,A)$ a pour sommets $S=\{pierre,feuille,ciseaux,puits\}$ et pour arêtes $A=\{(ciseaux,feuille),(feuille,puits),(feuille,pierre),(puits,pierre),(puits,ciseaux),(pierre,ciseaux)\}$.

Degré d’un sommet

Dans un graphe non-orienté, le degré d’un sommet $s$ est le nombre d’arêtes incidentes à ce sommet (une boucle comptant pour 2).
Dans le cas d’un graphe simple, on aura $d(s) = |Adj(s)|$ (nombre de sommets adjacents).

Dans un graphe orienté, le degré sortant d’un sommet $s$, noté $d_+(s)$, est le nombre d’arcs partant de $s$ (de la forme $(s,v)$ avec $s,v \in S$).
Dans le cas d’un graphe simple, on aura $d_+(s) = |Succ(s)|$ (nombre de successeurs).
De même, le degré entrant d’un sommet $s$, noté $d_−(s)$, est le nombre d’arcs arrivant en $s$ (de la forme $(v, s)$ avec $s,v \in S$).
Dans le cas d’un graphe simple, on aura $d_−(s) = |Pred(s)|$ (nombre de prédécesseurs).
Le degré d’un sommet $s$ d’un graphe orienté est donc la somme des degré entrant et sortant : $d(s) = d_+(s) + d_−(s)$.

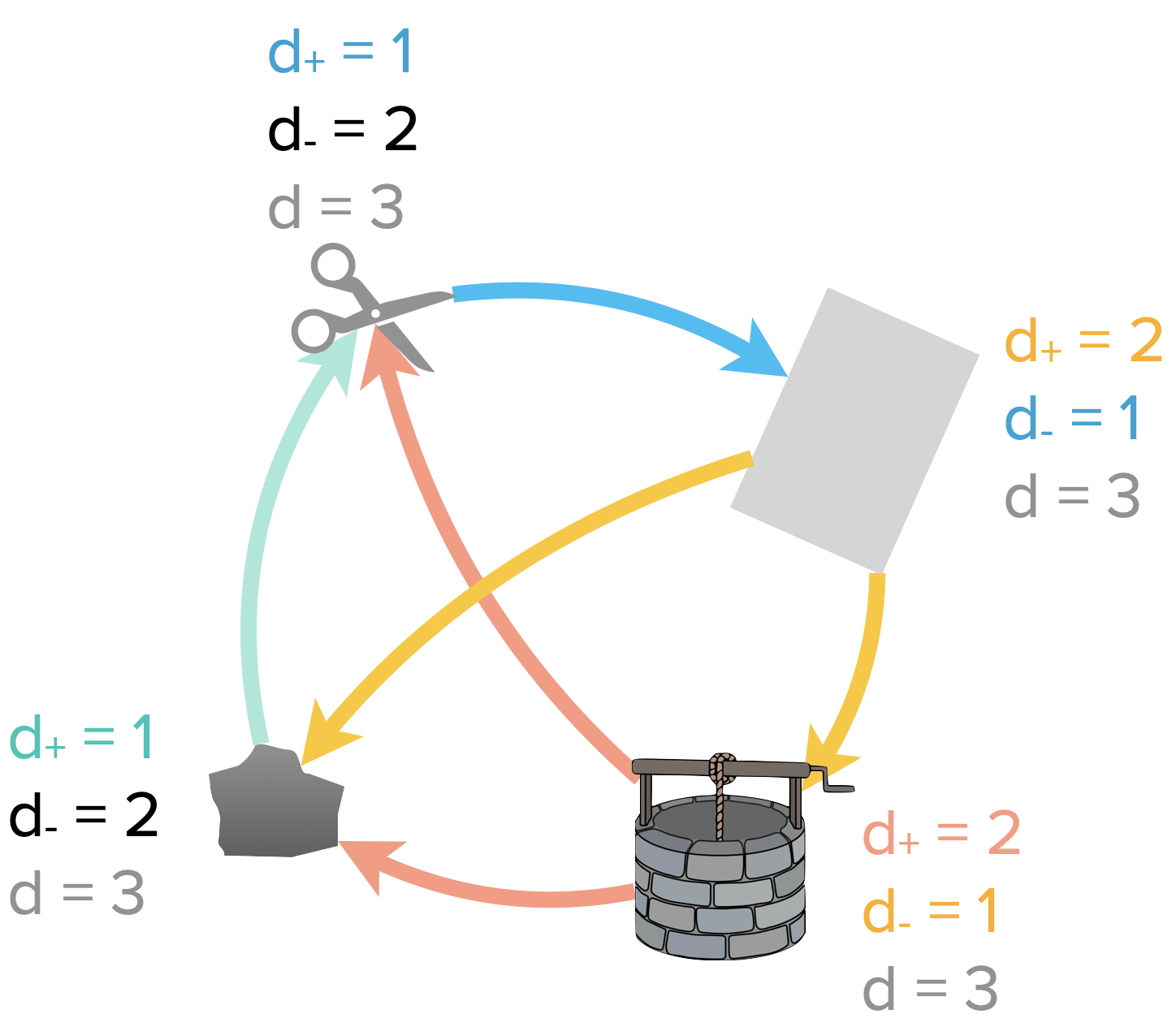Exemple : $d_+(puits)=2$ et $d_-(puits)=1$, d’où $d(puits) = d_+(puits) + d_−(puits)=2+1=3$

Pour tout graphe, la somme des degrés de chaque sommet est le double du nombre d’arêtes. $$\sum_{s \in S} d(s) = 2*|A|$$

$d(puits)=d(feuille)=d(ciseaux)=d(pierre)=3$ d’où $\sum_{s \in S} d(s) = 12$. Et on a bien $|A|=6$.

Et pour un graphe orienté, la somme des degrés entrant vaut la somme des degrés sortants et est aussi égal au nombre d’arêtes. $$\sum_{s \in S} d_+(s) = \sum_{s \in S} d_-(s) = |A|$$

	$d_+$	$d_-$
puits	2	1
feuille	2	1
ciseaux	1	2
pierre	1	2

$\sum_{s \in S} d_+(s) =\sum_{s \in S} d_-(s) =|A|=6$

On en déduit que pour tout graphe, il y a un nombre pair de sommets à degré impair.

Le degré d’un sommet est un concept simple, mais fécond, utilisé dans des contextes très différents. Dans un réseau social, le degré d’un sommet traduit l’importance d’une personne dans le groupe. Dans un réseau de communication comme Internet, on apprend beaucoup sur l’organisation réelle du réseau à partir de la distribution obtenue en ordonnant les sommets par leurs degrés.

Chemin, chaîne, cycle et circuit

Cas des graphes orientés

Soit $G = (S, A)$ un graphe orienté.

Un chemin d’un sommet $u$ vers un sommet $v$ est une séquence $< s_0,s_1,s_2,…,s_k >$ de sommets tels que $u = s_0$, $v = s_k$ et $(s_{i−1},s_i) \in A$ pour tout $i \in \{1,…,k\}$.
On dira que le chemin contient les sommets $s_0,s_1,…,s_k$ et les arcs $(s_0,s_1),(s_1,s_2),…,(s_{k−1},s_k)$.
La longueur du chemin est le nombre d’arcs dans le chemin, c’est-à-dire $k$.

S’il existe un chemin de $u$ à $v$, on dira que $v$ est accessible à partir de $u$.

Un chemin $< s_0,s_1,…,s_k >$ forme un circuit si $s_0 = s_k$ et si le chemin comporte au moins un arc ($k ≥ 1$).

Une boucle est un circuit de longueur $1$.

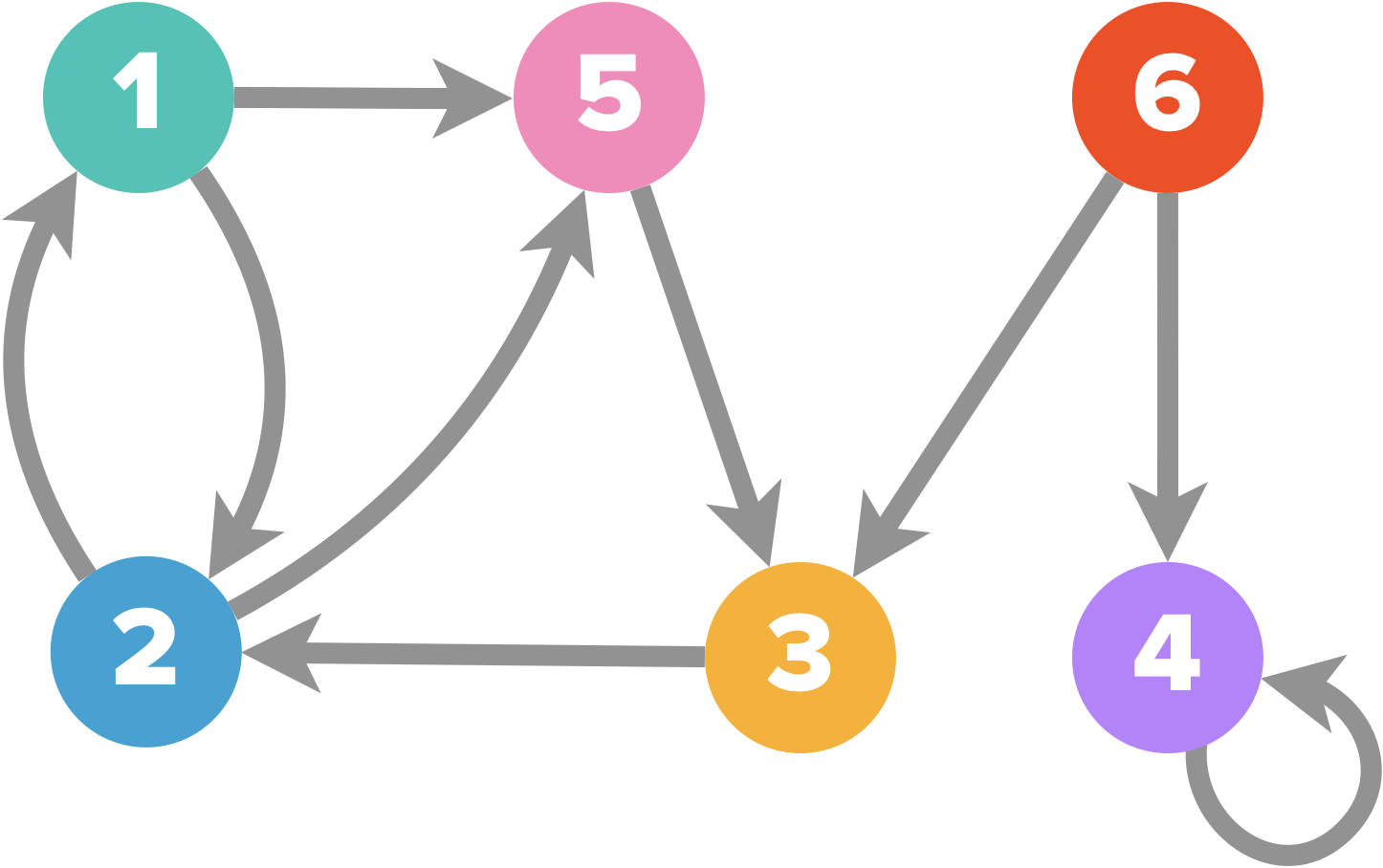
$<6,3,2,1>$ est un chemin du graphe.
$<1,5,3,2,1>$ est un circuit.

Cas des graphes non orientés

Si $G = (S, A)$ est un graphe non orienté, on parlera de chaîne au lieu de chemin, et de cycle au lieu de circuit.
Dans le cas d’un cycle, toutes les arêtes doivent être distinctes.
Un graphe sans cycle est dit acyclique.

Un arbre est est un graphe acyclique et connexe.

La ligne A du RER forme un arbre, mais pas la ligne C.

Distance dans un graphe

La notion de longueur de chemin nous permet ensuite de définir la notion de distance dans un graphe.

Soit un graphe $G=(S,A)$. La distance d’un sommet à un autre est la longueur du plus court chemin/chaîne entre ces deux sommets, ou $\infty$ s’il n’y a pas un tel chemin/chaîne :
$$ \forall x,y \in S,d(x,y)=\left\lbrace \begin{array}{ll} k \; &\text{si le plus court chemin de x vers y est de longueur k}\\ \infty &\text{sinon}\end{array}\right. $$

Le diamètre d’un graphe est la plus grande distance entre deux sommets.

Exemple : dans le graphe orienté ci-dessus $d(2,3)=2$, $d(3,2)=1$, $d(6,1)=3$ et $d(3,6)=\infty$.

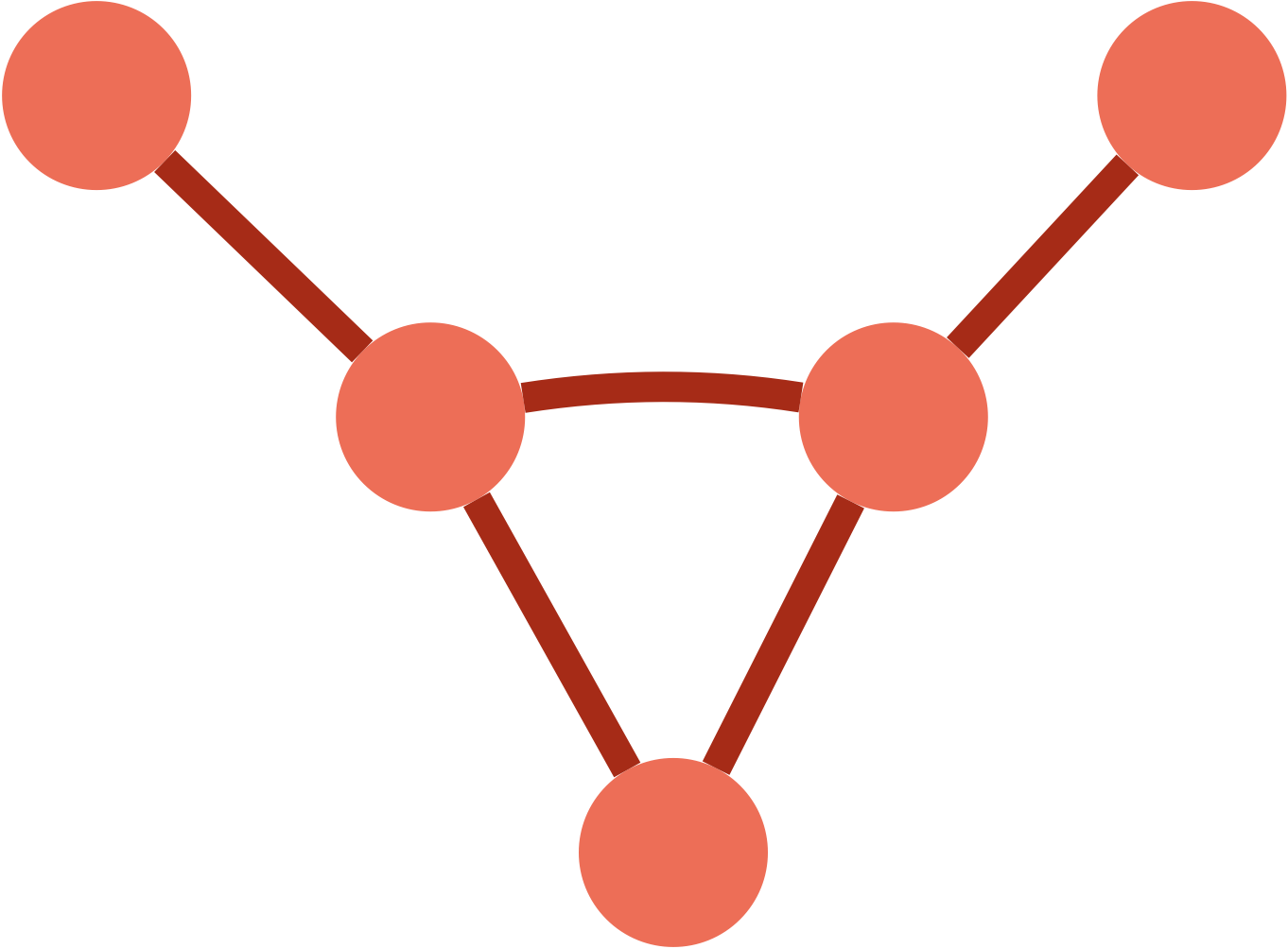
Dans ce graphe taureau, le diamètre vaut 3 (distance entre les deux cornes).

Connexité

Un graphe non orienté est connexe si chaque sommet est accessible à partir de n’importe quel autre (pour tout couple de sommets distincts $(s_i,s_j) \in S^2$, il existe une chaîne entre $s_i$ et $s_j$).

Le graphe comportant les sommets $1,2,3,4$ n’est pas connexe mais celui comportant les sommets $5,6,7,8$ l’est !

Représentation d’un graphe

Listes d’adjacence

Soit le graphe $G = (S,A)$ d’ordre $n$. On suppose que les sommets de $S$ sont numérotés de $1$ à $n$.

La représentation par listes d’adjacence de $G$ consiste en un tableau $T$ de $n$ listes (un par sommet) :
Pour chaque sommet $s_i \in S$, la liste d’adjacence $T[s_i]$ est une liste de tous les sommets $s_j$ tels qu’il existe un arc $(s_i,s_j) \in A$ ou une arête $\{s_i,s_j\} \in A$.
Autrement dit, pour chaque sommet, on liste ses voisins accessibles.

Dans chaque liste d’adjacence, les sommets sont généralement ordonnés arbitrairement.

Pour l’implémentation Python, on peut soit utiliser des listes imbriquées, soit un dictionnaire.

Exemple :

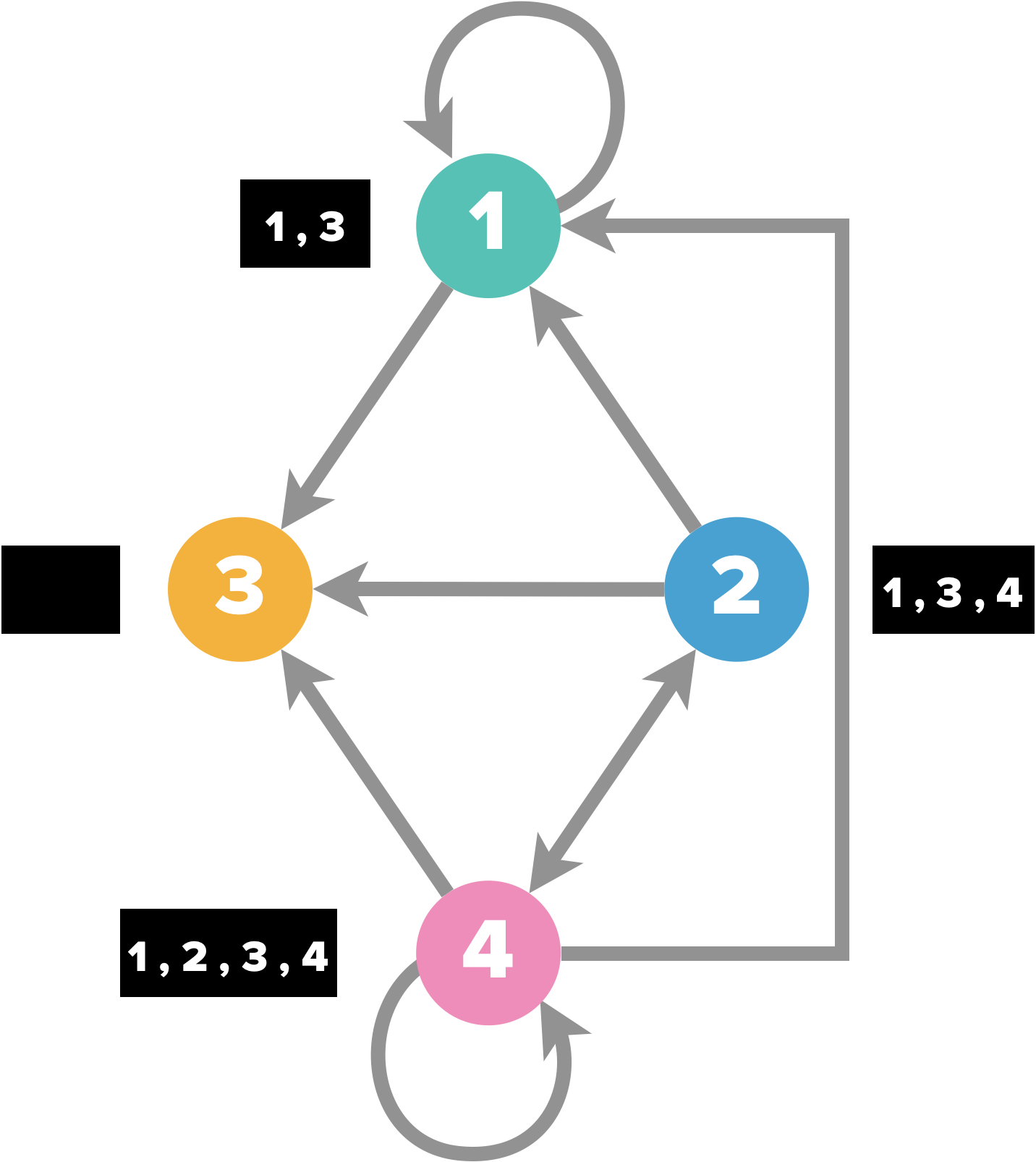
# Avec un dictionnaire
T = {1:[1,3],2:[1,3,4],3:[],4:[1,2,3,4]}
# Avec des listes imbriquées
T = [[1,3],[1,3,4],[],[1,2,3,4]]

L’avantage du dictionnaire est qu’il n’impose pas d’avoir une correspondance entre le numéro du sommet et la position dans la liste d’adjacence (dans le cas de listes imbriquées T[0] sera toujours la liste correspondant au premier sommet, T[1], celle du deuxième, etc.).

Taille mémoire nécessaire: si le graphe G est orienté, la somme des longueurs des listes d’adjacence est égale au nombre d’arcs de $A$, puisque l’existence d’un arc $(s_i,s_j)$ se traduit par la présence de $s_j$ dans la liste d’adjacence de $T[s_i]$.
En revanche, si le graphe n’est pas orienté, la somme des longueurs de toutes les listes d’adjacence est égale à deux fois le nombre d’arêtes du graphe, puisque si $\{s_i,s_j\}$ est une arête, alors $s_i$ appartient à la liste d’adjacence de $T[s_j]$, et vice versa.

Par conséquent, la liste d’adjacence d’un graphe ayant $n$ sommets et $m$ arcs ou arêtes nécessite de l’ordre de $O(n + m)$ emplacements mémoire.

Opérations sur les listes d’adjacence : pour tester l’existence d’un arc $(s_i, s_j)$ ou d’une arête $\{s_i, s_j \}$, on doit parcourir la liste d’adjacence de $T[s_i]$ jusqu’à trouver $s_j$.
En revanche, le calcul du degré d’un sommet, ou l’accès à tous les successeurs d’un sommet, est très efficace : il suffit de parcourir la liste d’adjacence associée au sommet.

D’une façon plus générale, le parcours de l’ensemble des arcs/arêtes nécessite le parcours de toutes les listes d’adjacence, et prendra un temps de l’ordre de $m$, où $m$ est le nombre d’arcs/arêtes.

Le calcul des prédécesseurs d’un sommet n’est pas pratique avec cette représentation. Il nécessite le parcours de toutes les listes d’adjacences de $T$.
Si l’on a besoin de connaître les prédécesseurs d’un sommet, une solution est de maintenir, en plus de la liste d’adjacence des successeurs, la liste d’adjacence des prédécesseurs.

Matrice d’adjacence

Soit le graphe $G = (S,A)$ d’ordre $n$. On suppose que les sommets de $S$ sont numérotés de $1$ à $n$.

La représentation par matrice d’adjacence de $G$ consiste en une matrice booléenne $M=(m_{i,j})$ de taille $n\times n$ telle que $m_{i,j} = 1$ si $ (i,j) \in A$, et $m_{i,j} = 0$ sinon.

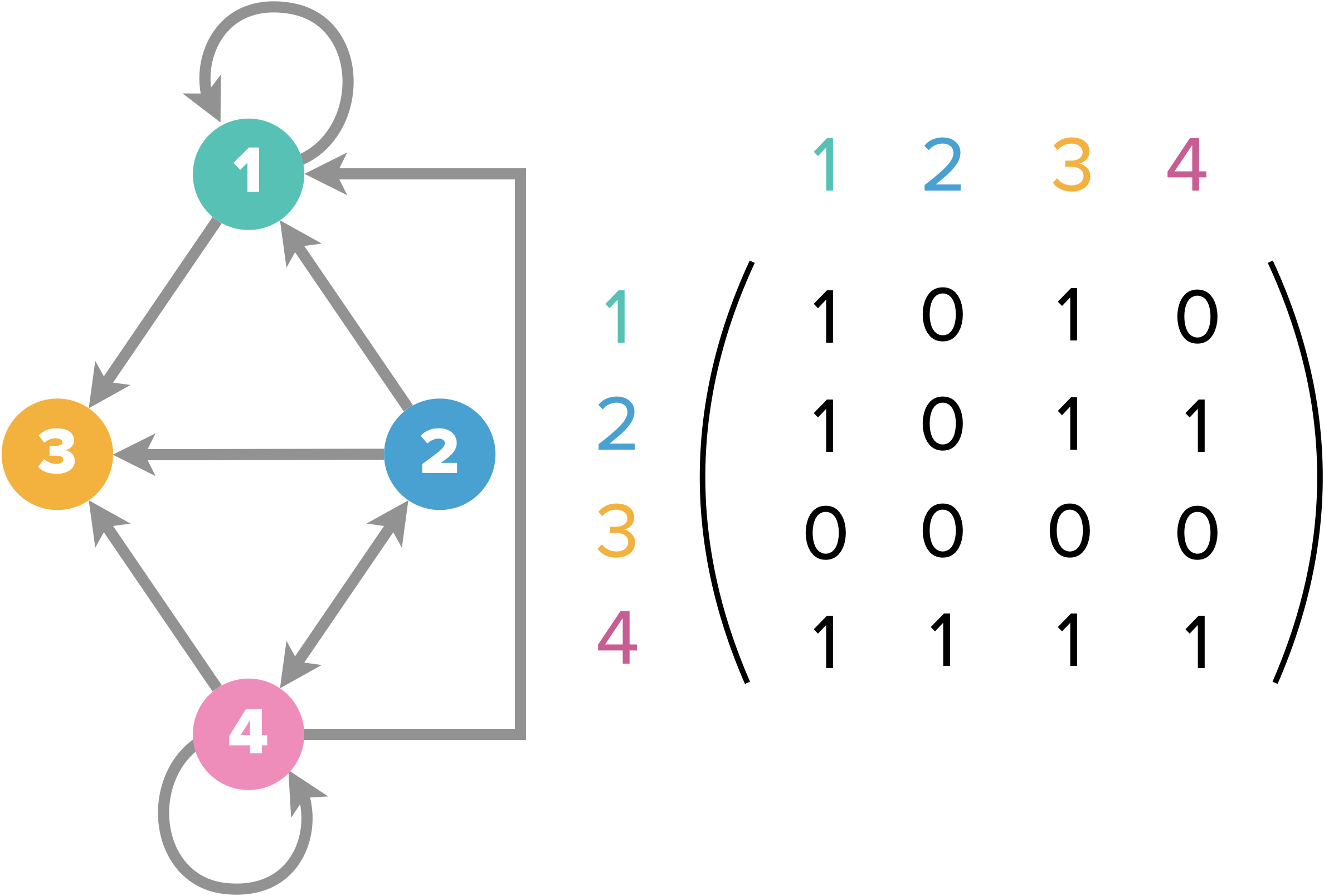
La matrice d’adjacence d’un graphe non orienté sera toujours symétrique, mais pas nécessairement celle d’un graphe orienté.

Implémentation Python :

M = [[1,0,1,0],[1,0,1,1],[0,0,0,0],[1,1,1,1]]
# pour savoir si un arc joint le sommet 1 au sommet 3
M[0][2]
# pour savoir si un arc joint le sommet 3 au sommet 1
M[2][0]

Taille mémoire nécessaire :

La matrice d’adjacence d’un graphe ayant $n$ sommets nécessite de l’ordre de $O(n^2)$ emplacements mémoire.
Si le nombre d’arcs est très inférieur à $n^2$ (on parle alors de graphe creux), cette représentation est loin d’être optimale.

Opérations sur les matrices d’adjacence :
le test de l’existence d’un arc ou d’une arête avec une représentation par matrice d’adjacence est immédiat (il suffit de tester directement la case correspondante de la matrice).
En revanche, connaître le degré d’un sommet nécessite le parcours de toute une ligne (ou toute une colonne) de la matrice.

D’une façon plus générale, le parcours de l’ensemble des arcs/arêtes nécessite la consultation de la totalité de la matrice, et prendra un temps de l’ordre de $n^2$.

Application : Combien y a-t-il de chemins menant d’un sommet à un autre en exactement $n$ coups ?

On cherche donc les chemins de longueur $n$ entre deux sommets $i$ et $j$.
Soit $M = (m_{i,j})$ la matrice d’adjacence d’un graphe $G(S,A)$. $M$ est donc aussi le nombre de chemin de $i$ à $j$ de longueur $1$ (une seul arête), que l’on va noter $m_{i,j}(1)$.
L’idée est alors de découper le chemin de longueur $n$ en un chemin de longueur $n-1$ suivi d’un chemin de longueur $1$. Le nombre $m_{i,j}(n)$ de chemins de longueur $n$ est ainsi donné par : $$ m_{i,j}(n)=\sum_{k=1}^{|S|}m_{i,k}(n-1)\times m_{k,j}(1)$$ Pour $ m_{i,j}(2) $, on obtient $m_{i,j}(n)=\sum_{k=1}^{|S|}m_{i,k}(1)\times m_{k,j}(1)$ qui n’est autre que $M^2$ (on reconnaît en effet la formule du produit matriciel).
Et par une récurrence immédiate, pour des chemins de longueur $n$, il suffit de calculer $M^n$.

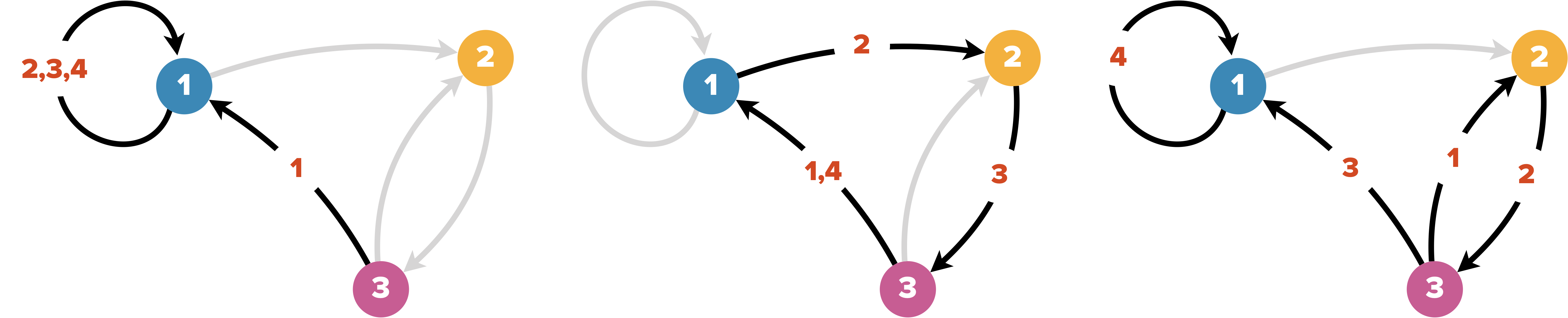
Exemple : combien y a-t-il de chemins de longueur 4 entre les sommets 1 et 3 du graphe représenté ci-dessous. La matrice d’adjacence du graphe vaut $M = \begin{pmatrix}1&1&0\\0&0&1\\1&1&0\end{pmatrix}$. Utilisons Python pour calculer $M^4$ :

import numpy as np # librairie très utile pour les calculs sur matrices
from numpy.linalg import matrix_power

M = [[1,1,0],[0,0,1],[1,1,0]]
M = np.array(M) # on convertit M en tableau numpy
M4 = matrix_power(M,4)
print(f"Il y a {M4[2][0]} chemins de longueur 4 du sommet 3 au sommet 1.")

Il y a 3 chemins de longueur 4 du sommet 3 au sommet 1.

Quelques comparaisons

	liste d’adjacence	matrice d’adjacence
Déterminer le degrés d’un sommet (graphe non orienté)	O(1)	O(n)
Determiner liste des successeurs / degrés sortant	O(1)	O(n)
Determiner liste des prédécesseurs / degrés entrant	O(m)	O(n)
Déterminer si un sommet S est relié directement à un autre	O(\|Succ(S)\|)	O(1)

Parcours d’un graphe

Pour déterminer si un sommet est accessible depuis un autre sommet, il faut pouvoir parcourir méthodiquement l’ensemble du graphe.

Algorithme de parcours en largeur (BFS)

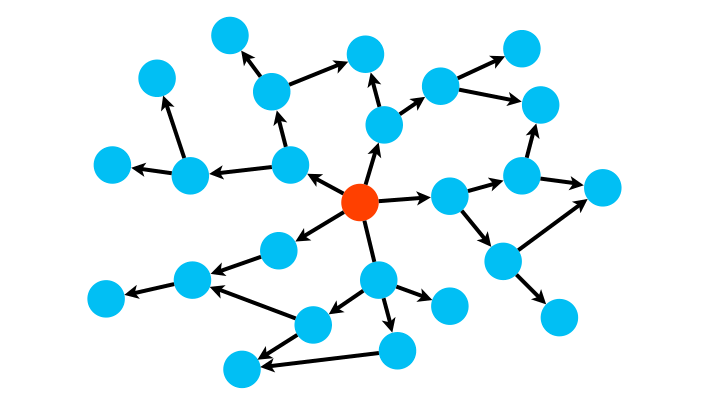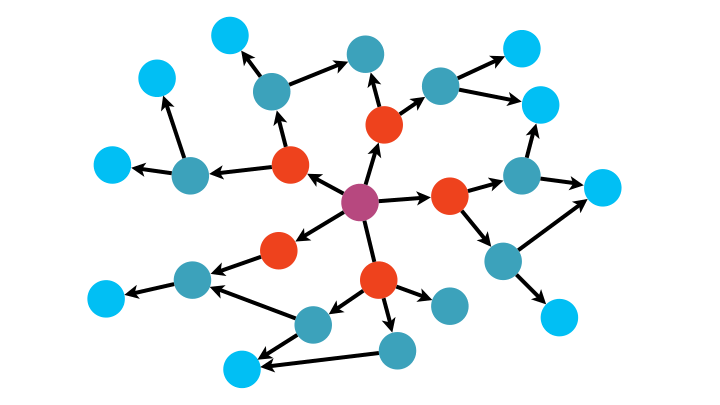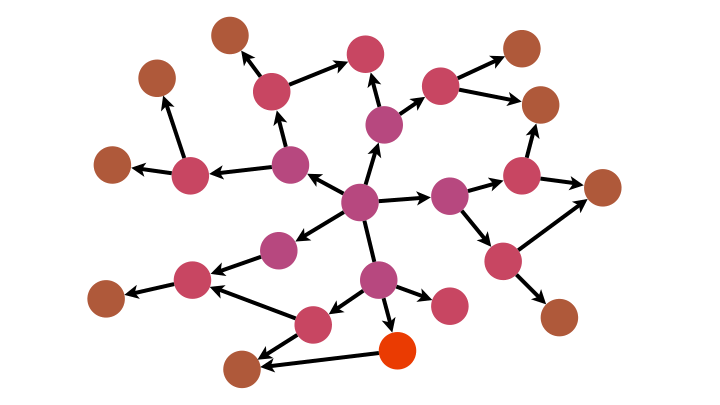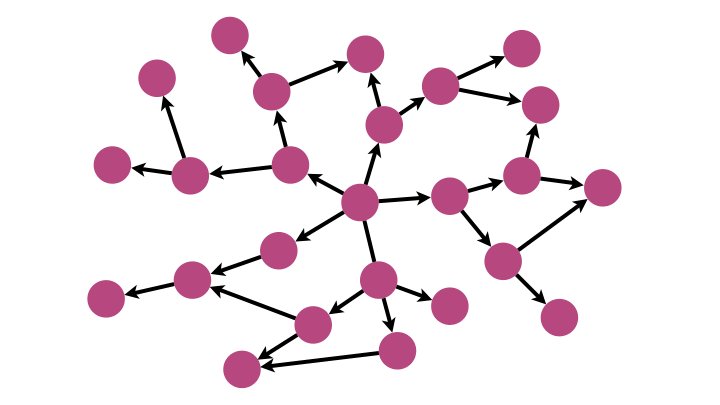
Une première méthode, l’algorithme de parcours en largeur (breadth-first BFS), consiste à partir d’un nœud, d’explorer tous ses successeurs, puis les successeurs de chacun de ses successeurs, etc., jusqu’à ce qu’il n’y ait plus de sommets.
Cela revient à inspecter le graphe par couche concentrique de plus en plus éloignées du nœud source.

Pour implémenter un tel algorithme, la structure de données adaptée est la file.

Les files (queues en anglais) sont des structures dynamiques (les éléments sont enfilés ou défilés) où, à l’instar d’une file d’attente à une caisse, c’est le premier arrivé qui est le premier retiré (FIFO pour “first in first out”). Les files sont utilisées par exemple lorsqu’il y a une possibilité d’encombrement (pour une imprimante partagée par exemple).

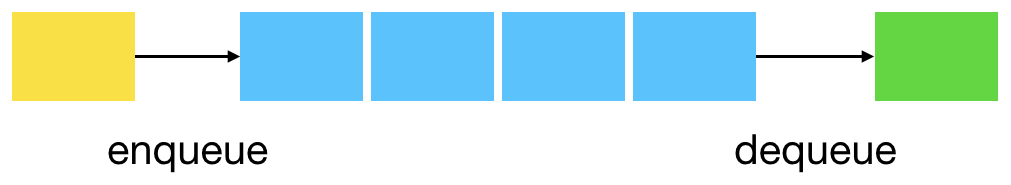
L’idée est de placer chaque nouveau successeur au bout d’une file (enfiler), puis de retirer un à un (défiler) les premiers arrivés (donc les plus proches du sommet de départ) lorsqu’ils sont à leur tour inspectés.

Pour l’implémentation des files, on pourrait utiliser des listes python en ajoutant toujours les éléments à la fin et les retirant au début, mais ce n’est pas très efficace. En effet, l’ajout d’un élément en début de liste à un coût linéaire (proportionnel à la taille de la liste). On aimerant pourtant tirer partie de la structure particulièrement simple des files où seule deux positions (première et dernière) nous intéressent…
Comme souvent en python, un module dédié, ici collecions.deque, va nous venir en aide. Il implément efficacement les files en permettant un enfilage et un défilage en temps constant.

G = {"Bob" : ["Alice","Dave","Charlie"],
     "Alice" : ["Elisa"],
     "Charlie" : ["Elisa","Hector"],
     "Dave" : ["Farid","Gus"],
     "Elisa" : [],
     "Farid" : [],
     "Gus" : [],
     "Hector" : []
     }

from collections import deque

# préconditions: on a besoin d'un graphe G(S,A) représenté par une liste d'adjacence implémentée par un dictionnaire et d'un sommet s de S
# postconditions : un sommet est accessible depuis s si et seulement si il est marqué comme "vu"
def parcours_largeur(G,depart):
    file = deque()
    file.append(depart)
    Vus = {s : False for s in G}
    Sommets = []
    while file: # tant que la file n'est pas vide
        sommet = file.popleft() # méthode de la classe deque permettant de défiler (équivaut à pop(0) sur une liste)
        if not Vus[sommet]: # évite ici d'avoir 2 Elisa, mais ça peut être bien pire
            file += G[sommet]
            Vus[sommet] = True
            Sommets.append(sommet) 
    return Sommets

parcours_largeur(G,"Bob") renvoie ['Bob', 'Alice', 'Dave', 'Charlie', 'Elisa', 'Farid', 'Gus', 'Hector'].

Si on ne marque pas les sommets vus (ici grâce au dictionnaire Vus), on se retrouve avec une boucle infinie dès qu’il y a un circuit ou un cycle (le simple graphe 🦉⇆🐘 par exemple).

Exemples d’applications du parcours en largeur :

utilisé par les robots d’exploration des moteurs de recherche pour construire l’index des pages web,
recherche dans les réseaux sociaux,
recherche d’un nœud voisin accessible dans les réseaux peer-to-peer.

Algorithme de parcours en profondeur (DFS)

L’idée de l’algorithme de parcours en profondeur (depth-first search DFS) est d’explorer jusqu’au bout chaque chaîne de successeurs du nœud source avant de passer à la suivante.
On n’explore alors plus par couches concentriques mais par branches.

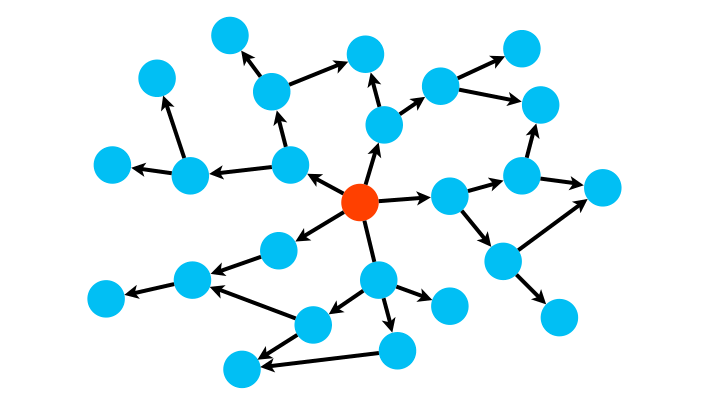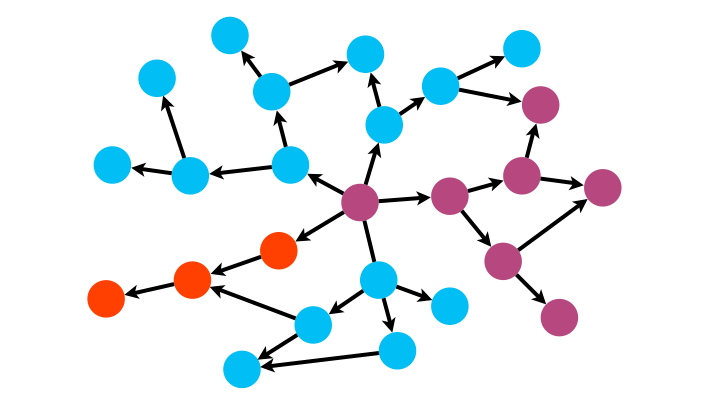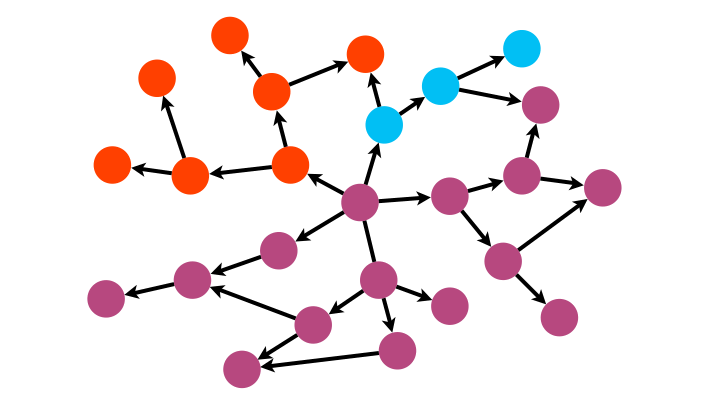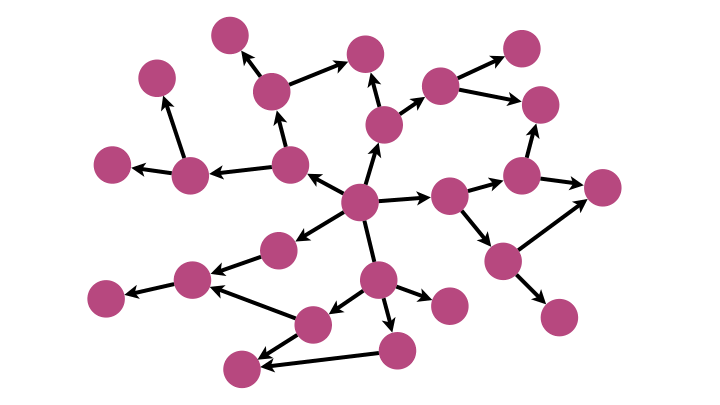
La structure de données dynamique adaptée est cette fois-ci la pile.

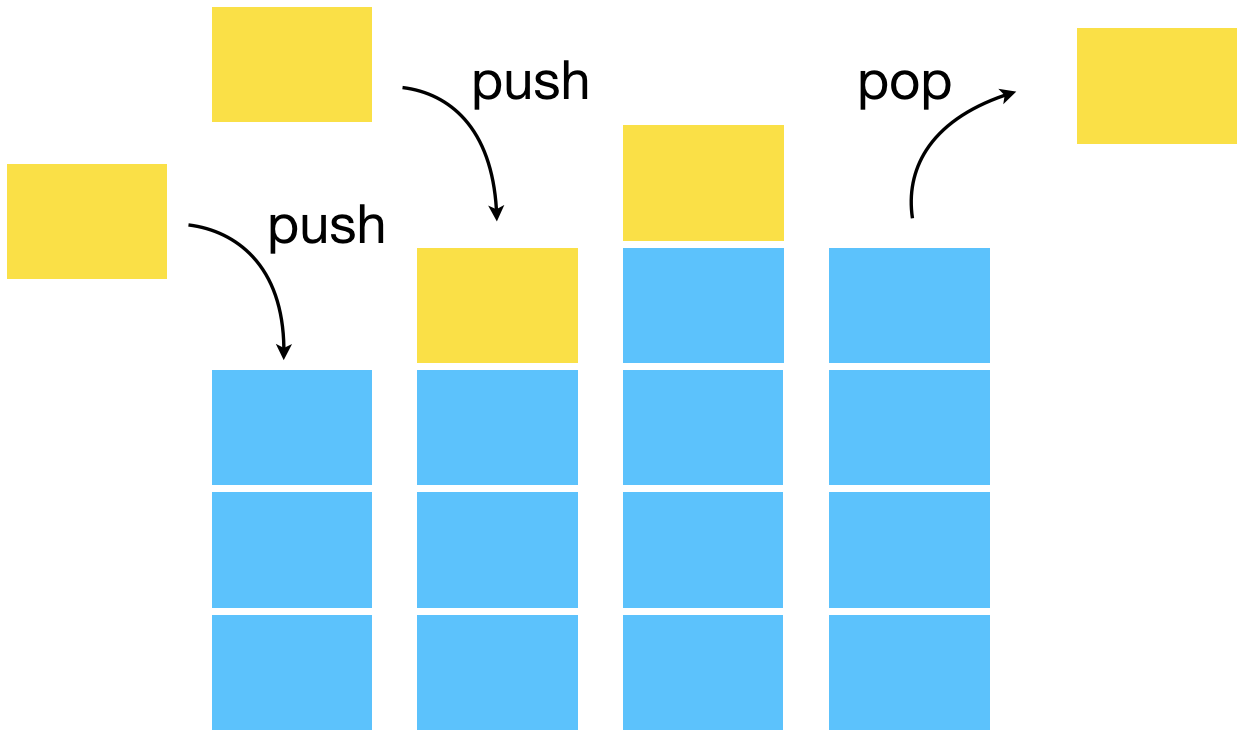
Les piles (stacks en anglais) sont des structures dynamiques (des éléments sont ajoutés = empilés, ou retirés = dépilés) ayant la propriété que l’élément extrait est celui qui y a été introduit le plus récemment (“dernier entré, premier sortie” ou LIFO “last in first out” en anglais). C’est l’équivalent informatique d’une pile d’assiettes. Cette structure est par exemple utilisée dans la fonction “annuler” (CTR-Z) d’un logiciel ou encore dans le traitement des fonctions récursives.

def parcours_profondeur(G,depart):
    pile = deque()
    pile.append(depart)
    Vus = {s : False for s in G}
    Sommets = []
    while pile:
        sommet = pile.pop()
        if not Vus[sommet]:
            pile += G[sommet]
            Vus[sommet] = True
            Sommets.append(sommet) 
    return Sommets

parcours_profondeur(G,"Bob") renvoie ['Bob', 'Charlie', 'Hector', 'Elisa', 'Dave', 'Gus', 'Farid', 'Alice'].

Exemples d’applications du parcours en profondeur :

trouver un chemin entre deux sommets,
détection de cycles dans un graphe,
utilisé dans le tri topologique,
trouver la sortie d’un labyrinthe.

La complexité des deux algorithmes est en $O(n+m)$ où $n =|S|$ et $m = |A|$.
En effet, la pile ou la file voit passer tous les successeurs ou adjoints de chaque sommet, ce qui correspond aux m arcs pour les successeurs et 2m pour les arêtes qui sont parcourues dans les deux sens. Comme chaque ajout et enlèvement de sommet se fait en $O(1)$, l’enfilement et défilement complet ainsi que l’empilement et dépilement complet sont en $O(m)$.
En plus de ces opérations, on modifie Vus et on construit Sommets, ce qui représente $O(n)$ nouvelles opérations.

Que deviendrait la complexité si on remplaçait l’utilisation d’un dictionnaire par celle d’une liste pour vérifier qu’un sommet a déjà été traîté (on utiliserait alors if sommet not in Sommets plutôt que if not Vus[sommet]) ?
Que deviendrait la complexité sans l’utilisation de la classe deque fournissant une vraie file/pile ?

Structures de données

On remarque que les deux algorithmes de parcours d’un graphe (BFS et DFS) ne diffèrent que par la structure de données utilisée. Et loin d’être anodin, ce passage de la file à la pile change complètement le principe du parcours !
Cela illustre bien que la conception d’un algorithme est intimement liée aux structures de données envisagées.

Une structure de donnée est une façon d’organiser les données de telle sorte que certaines opérations sur ces données (les primitives) soient très rapides. Une structure de données est donc spécialisée dans ces quelques opérations.
Lors de la conception d’un algorithme, l’identification des différentes opérations à effectuer va guider le choix de la structure de données adaptée.
Par exemple, l’algorithme de recherche en largeur doit gérer un ensemble où le premier élément ajouté doit toujours être le premier retiré (logique FIFO) $\rightarrow$ utilisation d’une file qui gère l’ajout d’un élément à la fin d’une file d’attente et l’extraction au début en temps constant (elle est optimisée pour ça, mais en contrepartie, elle ne sait faire que ça).
L’algorithme de recherche en profondeur suit lui la logique LIFO $\rightarrow$ utilisation d’une pile.
Dernier exemple : l’algorithme de Dijkstra (décrit plus loin) a besoin à chaque itération d’ajouter un élément à un ensemble et d’en retirer le plus petit élément $\rightarrow$ la file de priorité est la structure spécialisée dans ses opérations (dans quels autres algorithmes le tas pourrait-il être utilisé avantageusement ?).

Nous n’avions pas réellement besoin de la classe deque pour implémenter efficacement la pile. En effet, si insérer un élément au début d’une liste python de taille $n$ a bien un coût linéaire ($O(n)$) et ralentit donc l’exécution par rapport à l’utilisation d’une file, retirer un élément à la fin (via pop) se fait en temps constant ($O(1)$).

En pratique, on a utilisé dans les deux codes exactement le même objet, présent dans le module standard collections : deque().
deque() (qui se prononce comme deck) est l’implémentation d’une file d’attente à double extrémité (double-ended queue). Elle permet d’ajouter et retirer efficacement (en temps constant) des éléments aux deux extrémités. On peut donc bien à la fois s’en servir comme une file ou comme une pile.
On peut aussi utiliser deque() comme une liste python normale, mais l’accès d’un élément via son indice est alors inefficace (il ne se fait pas en temps constant). C’est la contrepartie de l’optimisation des opérations sur les extrémités…
Pour optimiser l’ajout et l’enlèvement aux extrémités, l’objet deque() utilise une liste doublement chaînée (chaque élément est stocké en mémoire avec deux pointeurs : un vers l’élément précédent et un vers le suivant).

La dernière note permet de pointer la distinction entre une structure de données abstraite (ou plutôt type de données abstrait TDA) et son implémentation :
Une liste doublement chaînée peut implémenter à la fois le TDA file ou pile.
Un tas (arbre binaire presque complet ordonné) permet d’implémenter le TDA file de priorité.

Graphes pondérés

Dans de nombreuses situations, les arêtes d’un graphe ne sont pas toutes équivalentes. On ajoute alors l’information du “coût” que cela représente d’emprunter telle ou telle arête. On appelle poids ces valeurs ajoutées aux arêtes/arcs.

Par exemple, pour modéliser un réseau ferroviaire, on peut attribuer à chaque arête modélisant les jonctions entre deux gares la distance correspondante. Et pour un réseau de communication, le poids d’une arête correspondra plutôt au temps nécessaire pour transférer un message de taille élémentaire.

On obtient alors un graphe pondéré.

On utilise par exemple des graphes pondérés, plus particulièrement des arbres de probabilité (où chaque branche est affublée d’une probabilité) pour calculer des probabilités conditionnelles.

Exemple :

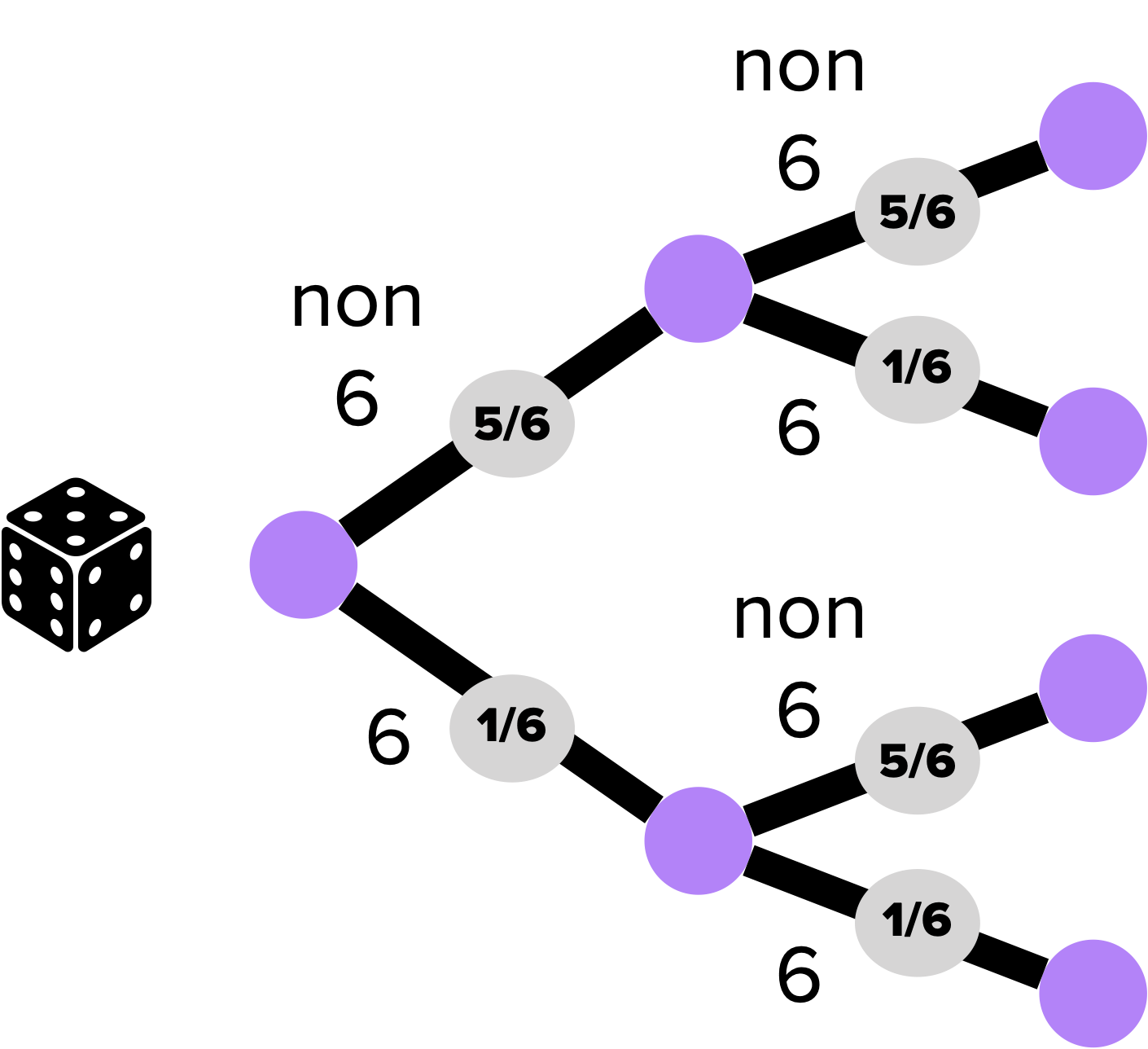
Très souvent (particulièrement pour les réseaux de communication), l’information ajoutée au graphe est un temps ou une distance et se pose alors le problème de l’optimisation d’un trajet entre deux sommets.

Le poids d’un chemin est la somme des poids des arcs empruntés.

La distance entre deux sommets (dans un graphe pondéré) correspond au chemin de poids minimum entre ces deux sommets.

Problème du plus court chemin

Pas au programme de TSI mais plus prudent d’en avoir entendu parler pour l’épreuve de Centrale qui jusqu’à maintenant était commune aux autres sections.

Si le graphe considéré n’est pas pondéré, l’algorithme de parcours en largeur, moyennant quelques adaptations, est tout à fait capable de faire le travail.

Algorithme de parcours en largeur

Comme l’algorithme de parcours en largeur examine le graphe en couches concentriques depuis le sommet de départ, lorsqu’il parvient au sommet cible, on est sûr que le nombre d’arcs est minimal.

Il suffit alors de joindre à la liste des sommets examinés, la liste des chemins permettant de parvenir à chacun de ces sommets (en incrémentant à chaque tour chacun des chemins du sommet correspondant de la nouvelle couche).

def recherche_largeur(G,depart,arrivee):
    file = [(depart,[depart])] # on remplace la file des sommets par une file de tuples (sommet,chemin)
    Vus = {s : False for s in G}
    while file:
        sommet,chemin = file.pop(0) # pop(0) fait la même chose que le popleft des deque
        if sommet == arrivee:
            return chemin # si l'arrivée est atteinte, on retourne le chemin correspondant
        if not Vus[sommet]:
            for s in G[sommet]:
                nv_chemin = chemin+[s]
                file.append((s,nv_chemin))
            Vus[sommet] = True 
    return False # si l'arrivée n'est pas atteinte, on renvoie Faux

G = {"Minimes" : {"Tasdon","Hôpital"},
     "Hôpital" : {"Verdun"},
     "Verdun" : {"Stade"},
     "Tasdon" : {"Cognehors", "Lafond"},
     "Cognehors" : {"Verdun"},
     "Lafond" : {"Mireuil"},
     "Mireuil" : {"Stade"},
     "Stade" : {}
     }

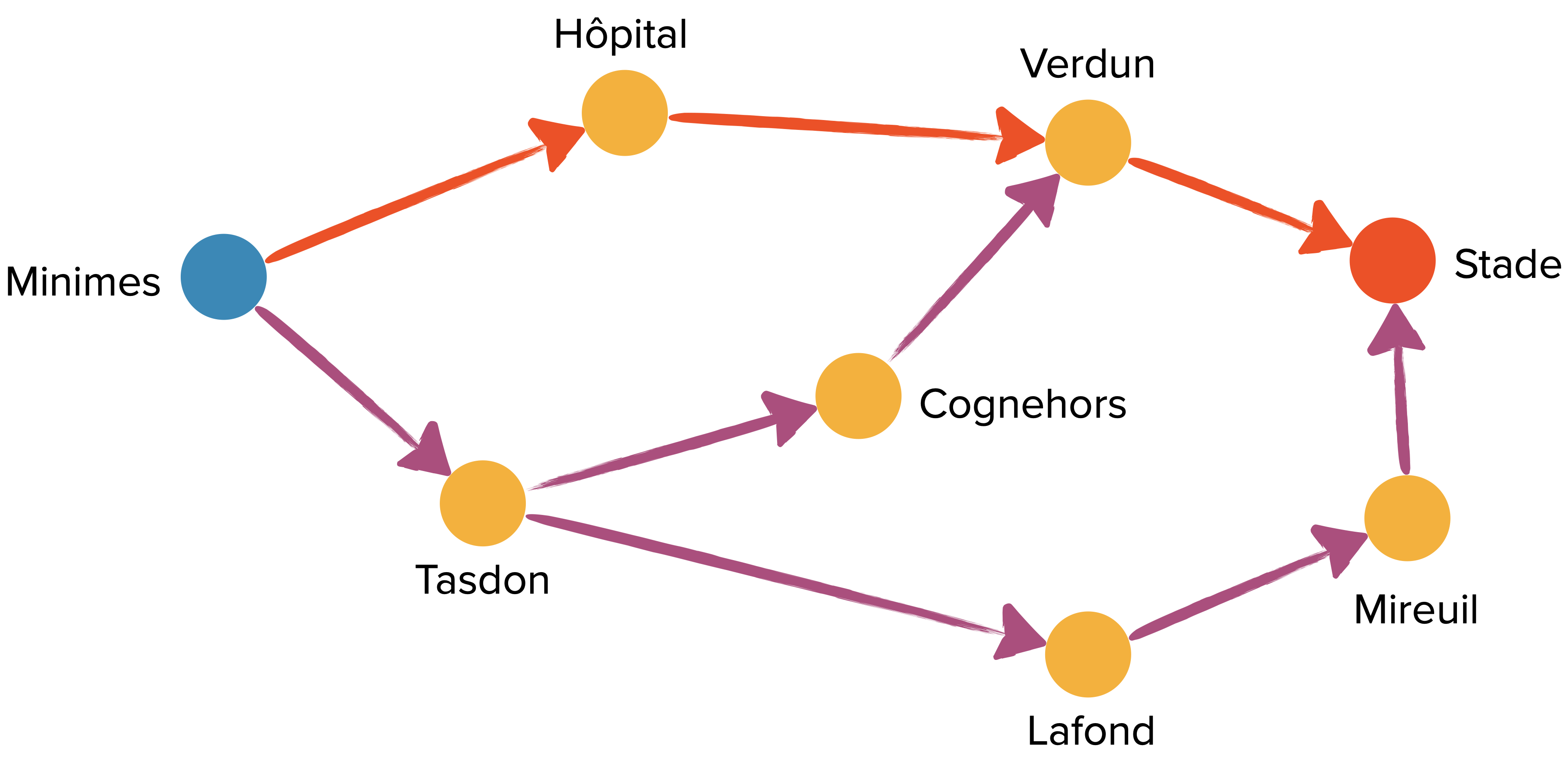
recherche_largeur(G,"Minimes","Stade") retourne bien le chemin comportant le moins d’arêtes : ['Minimes', 'Hôpital', 'Verdun', 'Stade'].

Mais si on ajoute des poids, l’algorithme de recherche en largeur devient inefficace puisqu’il se borne à donner la même réponse (les pondérations sont nulle part prises en compte !).

G_pond = {"Minimes" : {"Tasdon": 5,"Hôpital": 4},
          "Hôpital" : {"Verdun": 21},
          "Verdun" : {"Stade": 4},
          "Tasdon" : {"Cognehors": 7, "Lafond": 7},
          "Cognehors" : {"Verdun": 8},
          "Lafond" : {"Mireuil": 5},
          "Mireuil" : {"Stade": 3},
          "Stade" : {}
          }

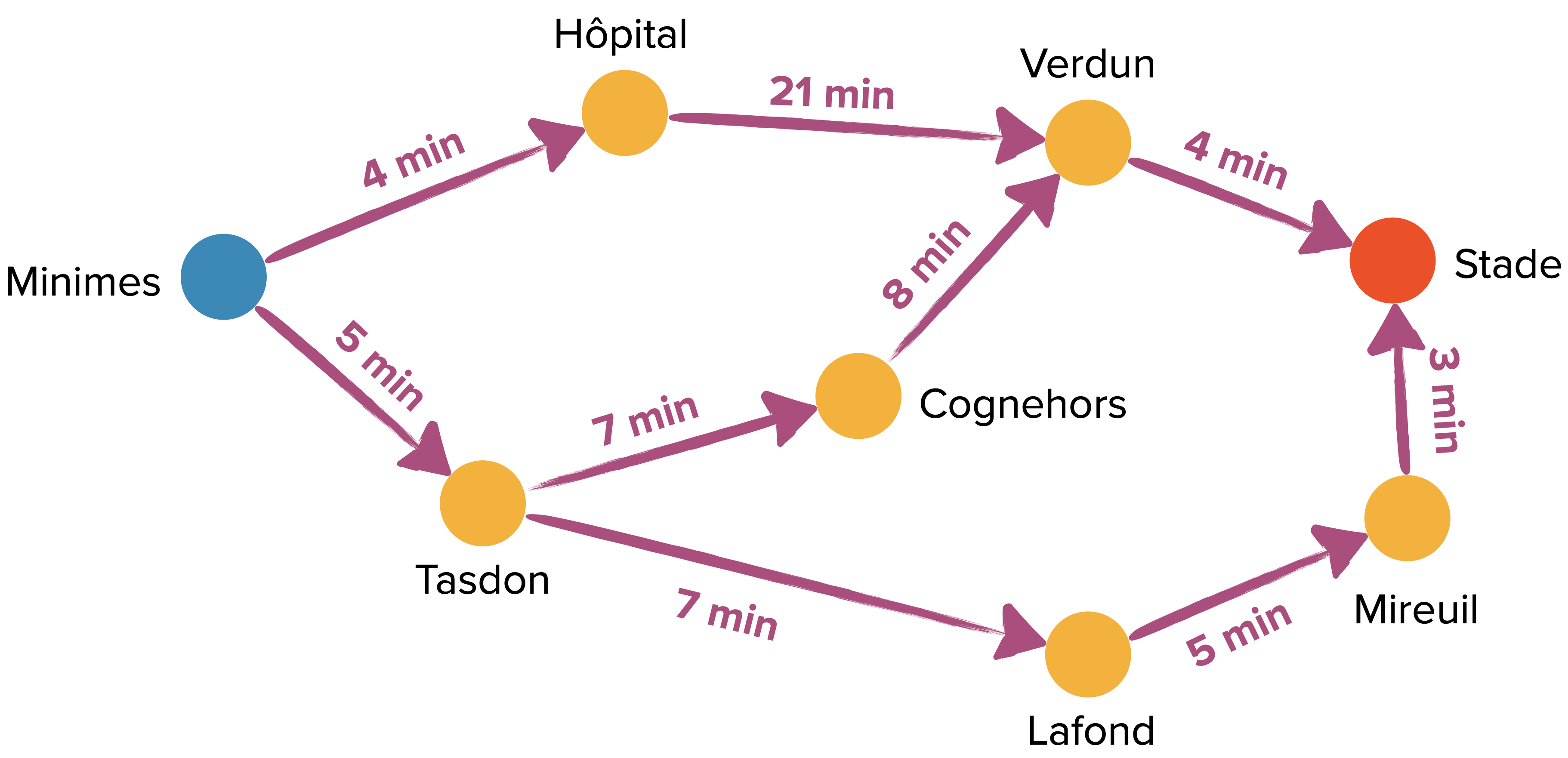
recherche_largeur(G_pond,"Minimes","Stade") retourne à nouveau ['Minimes', 'Hôpital', 'Verdun', 'Stade'] alors qu’il y a maintenant des chemins plus rapides !

Algorithme de Dijkstra

L’algorithme de Dijkstra va permettre de dépasser les limites du parcours en largeur grâce à un score attribué à chaque sommet (au départ, tous les scores sont fixés à l’infini sauf celui du sommet de départ, fixé à zéro). En sortie de l’algorithme, chaque score vaudra la distance entre le sommet et le sommet de départ.

Comme avec les parcours en largeur et en profondeur, la distinction principale réside dans la sélection du prochain sommet ajouté à Vus ; il s’agit maintenant de celui ayant le plus petit score parmi les sommets non déjà inspectés.

On appelle algorithme glouton un algorithme dont la logique consiste à choisir à chaque itération un objet de valeur maximale ou minimale.
Dijkstra est donc un exemple d’algorithme glouton.

À chaque sommet ajouté $s$, on met à jour les scores de chaque successeur $s_+$ en gardant la valeur minimale entre le score qu’il avait précédemment et la somme entre le score de $s$ et le poids de l’arc $(s,s_+)$ (c’est l’étape de relaxation des arêtes) : $\text{score}(s_+)=\min\left(\text{score}(s_+),\text{score}(s)+p((s,s_+))\right)$

Et en gardant à chaque mise-à-jour du score la trace du nouveau prédécesseur, on obtient un algorithme capable de fournir les distances et les plus courts chemins entre le sommet de départ et tous les autres.

Idée clé de l’algo : si un chemin entre deux sommets est le plus court alors tout chemin intermédiaire entre des sommets présents sur le chemin principal est aussi le plus court entre ces sommets. Cela permet de construire le chemin le plus court de proche en proche.

Ce n’est plus vrai s’il y a une arête négative : un plus court chemin n’a alors plus à être composé des tronçons les plus courts entre les sommets intermédiaires.
Moralité, la correction partielle de l’algorithme de Dijkstra suppose que tous les poids des arêtes du graphe sont positifs.

# préconditions : un graphe orienté pondéré G(S,A) avec des poids positifs pour chaque arc représenté par une liste d’adjacence grâce à un dictionnaire, un sommet s_0 de S

# postcondition : pour chaque sommet s_i de S le score trouvé correspond bien à la distance entre s_0 et s_i (d(s_0,s_i))

def sommet_suivant(scores,nonvus):
    """
    retourne le sommet de nonvus au plus bas score
    """
    plus_bas_score = float("inf")
    sommet_choisi = None
    for sommet in nonvus:
        score = scores[sommet]
        if score < plus_bas_score:
            plus_bas_score = score
            sommet_choisi = sommet
    return sommet_choisi

def Dijkstra(G,depart):
    # on construit Scores et Preds  dans lesquels on mettra à jour les scores calculés et les prédecesseurs des sommets examinés
    Scores = {}
    Preds = {}
    # initialisation
    for s in G:
        Scores[s] = float("inf")
        Preds[s] = None
    Scores[depart] = 0
    NonVus = list(G.keys()) # liste pour stocker les sommets examinés
    sommet = depart 
    while sommet is not None:
        score = Scores[sommet]
        Succ = G[sommet]
        for n in Succ:
            nv_score = score + Succ[n]
            if Scores[n] > nv_score:
                Scores[n] = nv_score
                Preds[n] = sommet
        NonVus.remove(sommet)
        sommet = sommet_suivant(Scores,NonVus)
    return Preds,Scores

preds,scores = Dijkstra(G_pond,"Minimes")
print(preds)
print(scores)

# Ce qui s'affiche :

{'Minimes': None, 'Hôpital': 'Minimes', 'Verdun': 'Cognehors', 'Tasdon': 'Minimes', 'Cognehors': 'Tasdon', 'Lafond': 'Tasdon', 'Mireuil': 'Lafond', 'Stade': 'Mireuil'}
{'Minimes': 0, 'Hôpital': 4, 'Verdun': 20, 'Tasdon': 5, 'Cognehors': 12, 'Lafond': 12, 'Mireuil': 17, 'Stade': 20}

La complexité de cette implémentation de l’algorithme de Dijkstra est en $O(n^2)$ où $n=|S|$ est le nombre de sommets du graphe.

En effet, deux actions sont réalisées dans la boucle principale qui parcourt chaque sommet :

La recherche du sommet non validé ayant un score minimal et sa validation. Elle se fait via la fonction sommet_suivant qui est en $O(n)$.
La mise à jour des scores des sommets. Elle se fait en temps constant mais concerne tous les successeurs du sommet étudié.

On obtient : $$\sum_{u\in S}\left(T(\text{obtenir le sommet min et le retirer})+\left(\sum_{v\in Succ(u)}T(\text{mettre à jour le score})\right)\right) = O(n^2+m) = O(n^2)$$

Comme évoqué plus haut, on peut améliorer la complexité en utilisant une structure de données adaptée au problème : la file de priorité implémentée par un tas.
L’idée est d’optimiser le choix du prochain sommet inspecté, celui au plus bas score parmi les sommets pas encore validés. En effet, réinspecter systématiquement toute la liste des sommets restants (c’est ce que fait la fonction sommet_suivant) gaspille de l’information. C’est sur ce point que le tas vient à la rescousse :
le tas est une structure de données de type arbre qui permet de retrouver directement l’élément que l’on veut traiter en priorité. Le tas garde en permanence le sommet de plus bas score en son sommet avec un coût logarithmique.

Conséquence : si on remplace la fonction sommet_suivant par un tas et ses opérations dédiées d’ajout et d’extraction, on passe d’une complexité linéaire à une complexité logarithmique pour cette opération.

import heapq # module implémentant un tas (heap en anglais)

def Dijkstra_tas(G, depart):
    Scores = {sommet: float('infinity') for sommet in G}
    Preds = {sommet: None for sommet in G}
    Scores[depart] = 0
    tas = [(0, depart)]
    # liste de tuples contenant le score et le sommet associé
    # le score correspond alors à la priorité du tas
    while tas:
        score_actuel, sommet_actuel = heapq.heappop(tas)
        # on retire le sommet prioritaire du tas
        if score_actuel == Scores[sommet_actuel]:
        # permet de vérifier que le sommet correspond bien à la dernière mise-à-jour        
            score_voisins = G[sommet_actuel]
            for voisin in score_voisins:
                score = score_actuel + score_voisins[voisin]
                if score < Scores[voisin]:
                    Scores[voisin] = score
                    Preds[voisin] = sommet_actuel
                    heapq.heappush(tas, (score, voisin))
                    # on ajoute le score et le sommet au tas
                    # le même sommet peut être ajouté plusieurs fois avec des scores différents
    return Preds,Scores

Grâce au tas, la complexité de Dijkstra est maintenant en $O(m\log n)$ où $n =|S|$ et $m = |A|$.

En effet, le tas contient $O(m)$ éléments (les voisins mis-à-jour), donc les opérations heappop et heappush sont en $O(\log m)=O(\log n)$.

Comme un graphe simple contient au plus $\binom{n}{2}=\frac{n(n-1)}{2}$ arêtes et le double pour les arcs, on en déduit que $O(m)=O(n^2)$.
Et donc $O(\log m)=O(2\log n)=O(\log n)$.

On entre au pire $m$ fois dans la boucle while, mais la boucle for n’est exécutée que $n$ fois car la condition score_actuel <= Scores[sommet_actuel] nous assure de ne traiter qu’une seule fois chaque sommet. $$\sum_{O(m)}T(\text{retirer la racine du tas})+\sum_{u \in S}\left(\sum_{v\in Succ(u)}\left(T(\text{mettre à jour le score})+T(\text{placer dans le tas})\right)\right)= O(m\log n+m\log n) = O(m \log n)$$

Cette implémentation n’est réellement avantageuse que si le graphe est creux (pour ne pas avoir $|A|$ de l’ordre de $|S|^2$). Mais même si le tas contient au pire de l’ordre de $|A|$ éléments, c’est en pratique quasiment jamais le cas puisqu’il faudrait qu’à chaque arête parcourue lors de l’inspection des voisins, il y ait mise à jour du score d’un sommet (pour provoquer son ajout au tas).

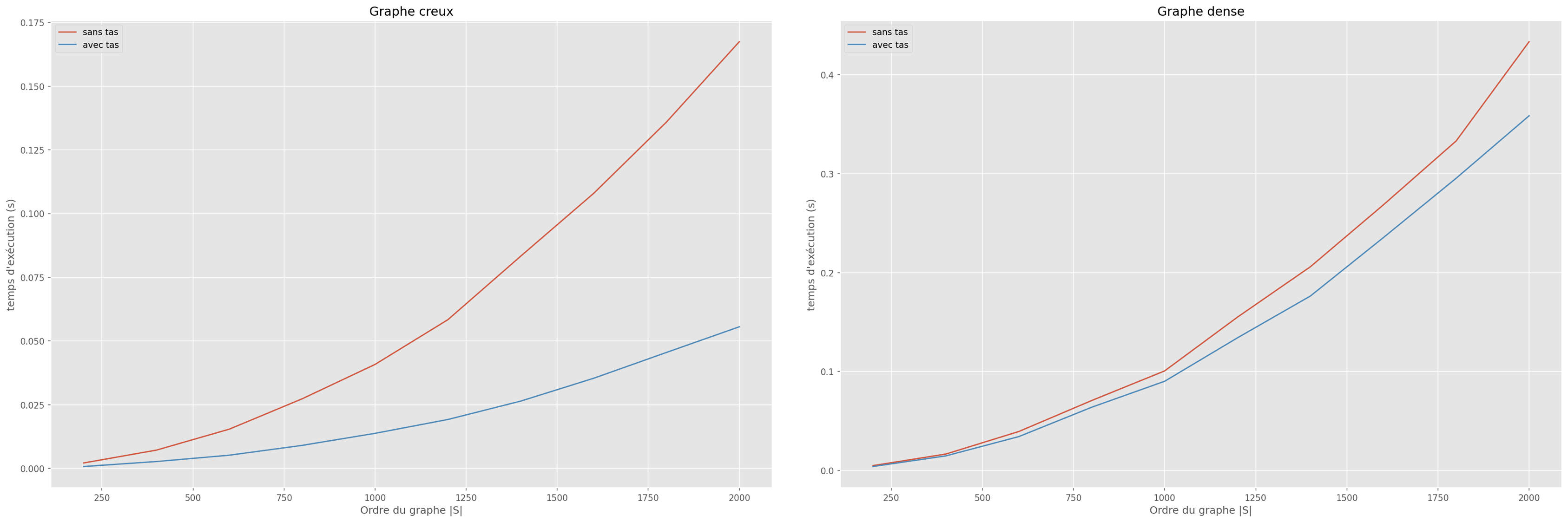
On verra dans le TP comment encore améliorer les choses grâce à l’utilisation d’une heuristique. On passe alors de l’algorithme de Dijkstra à l’algorithme A* (A star ou A étoile).

Dans une lettre de 1856, Hamilton écrit : “I have found that some young persons have been much amused by trying a new mathematical game which the Icosion furnishes, one person sticking five pins in any consectutive points […] and the other player then aiming to insert, which by the theory in this letter can always be done, fifteen other pins, in cyclical succession, so as to cover all the other points, and to end in immediate proximity to the pin wherewith his antagonist had begun.” ↩︎