Représentation des nombres
Comment un nombre est-il représenté à l’intérieur d’un ordinateur ?
L’espace pour représenter un nombre en machine est limité. Si cette limitation n’a pas trop d’impact pour les entiers (surtout en Python !) elle devient très handicapante pour représenter les réels.
La représentation machine d’un nombre est appelée mot machine. Sa taille est généralement aujourd’hui de 64 bits.
Les différentes bases
Une écriture en base $b$ utilise $b$ chiffres différents :
- 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9 pour la base décimale
- 0 et 1 pour la base binaire
- 0, 1, 2, 3 pour la base 4
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E et F pour la base hexadécimale
Un nombre $a$ écrit dans une basse $b$ se note $(a_n a_{n-1}\cdots a_0)_b$ avec $(a_n a_{n-1}\cdots a_0)_b = a_n\times b^n + a_{n-1} \times b^{n-1}+ \cdots + a_0 = \sum\limits_{i=0}^{n} a_i\,b^i$
Conversions
La conversion d’une base à une autre n’est pas un objectif de formation d’après le B.O. Néanmoins, la comparaison et les pièges des algorithmes qui suivent dépassent le simple enjeu de la conversion. Moralité, pas besoin d’apprendre par cœur ces algorithmes, mais leur étude est conseillée.
- Pour convertir un nombre d’une base $b<10$ vers la base 10 :
Il suffit de calculer la somme précédente (si $b>10$, il faut en plus donner la valeur des nouveaux chiffres).
Comparaison de deux algorithmes :
- Algorithme classique :
def convbvers10(a: str, b: int) -> int:
"""
Convertit a de la base b à la base 10
le nombre à convertir a doit être passé en argument
sous la forme d'une chaine de caractères 'a_n...a_0'
b, la base, est un entier inférieur à 10.
La fonction retourne un entier en base 10.
"""
s = 0
n = len(a)-1
for e in a:
s += int(e)*b**n
n -= 1
return s
convbvers10('100101101',2)
301
convbvers10('10231',4)
301
- Méthode de Horner (qui utilise des multiplications imbriquées) :
$a = ((((a_nb+a_{n-1})b+a_{n-2})b+\cdots)b+a_1)b+a_0$
Implémentée en Python, cela donne :
def convbvers10_Horner(a: str, b: int) -> int:
"""
Convertit a de la base b à la base 10 en utilisant la méthode de Horner
le nombre à convertir a doit être passé en argument
sous la forme d'une chaine de caractères 'a_n...a_0'
b, la base, est un entier inférieur à 10.
La fonction retourne un entier en base 10.
"""
s = 0
for i in range(0,len(a)):
s = s*b + int(a[i])
return s
convbvers10_Horner('100101101',2)
301
Lequel de ces deux algorithmes est le plus eficace ?
la fonction Python native int() permet aussi de convertir un nombre écrit dans une base $b$ vers la base décimale en ajoutant $b$ en argument.
int('10231',4)
301
- Pour convertir de la base 10 vers la base $b$ :
On peut remarquer que le quotient de la division euclidienne de $a=(a_n a_{n-1}\cdots a_0)_b$ par $b$ vaut $(a_n a_{n-1}\cdots a_1)_b$ et que le reste vaut $a_0$. De même, le quotient de la division euclidienne de $(a_n a_{n-1}\cdots a_1)_b$ par $b$ vaut $(a_n a_{n-1}\cdots a_2)_b$ et le reste vaut $a_1$. Et on continue tant que le quotient est non nul. On obtient ainsi la décomposition de $a$ dans la base $b$.
Un algorithme en découle naturellement :
def conv10versb(a,b) :
"""
Arguments : nombre à convertir et base cible
la fonction retourne une chaîne de caractère
correspondant au nombre a dans la base b.
"""
s = ''
while a > 0:
s = str(a%b) + s # le dernier terme est ajouté à gauche de la chaîne !
a //= b
return s
conv10versb(301,2)
'100101101'
les fonctions Python natives bin() et hex() permettent de convertir directement un nombre de la base 10 vers les bases respectives 2 et 16 (ces fonctions retournent des chaînes de caractères).
bin(301,2)
'0b100101101'
Usages des différentes bases
- La base binaire :
C’est la base naturelle de l’ordinateur. Avec ses deux caractères (0 et 1), c’est la seule que peut adresser directement un ordinateur dont la nature même n’est qu’interrupteurs, passant ou non. Chaque bit est un chiffre binaire.
En base 2, les calculs sont facilités et la plupart des algorithmes scolaires des opérations de base marchent, voir sont simplifiés.
Prenons l’exemple de la multiplication : chaque 1 du second facteur décale le premier facteur d’autant de rangs que son propre rang dans le second facteur, puis on additionne entre eux tous les différents termes obtenus (on utilisera cette méthode dans l’algorithme de multiplication égyptienne du TP8) .
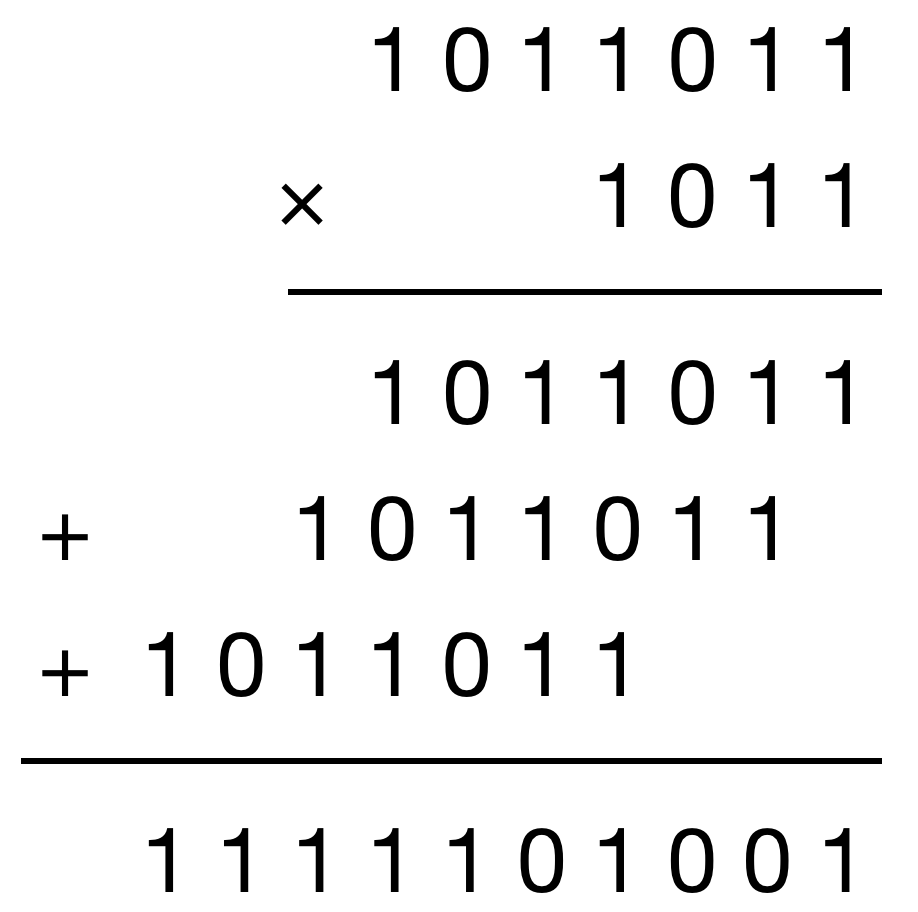
En Python, on peut écrire un nombre directement en base 2 si on le précède des caractères 0b.
a = 0b1011011
b = 0b1011
a*b
bin(a*b)
'0b1111101001'
- La base hexadécimale :
La base 16 joue un rôle particulier en informatique. Pour quelle raison ? L’écriture binaire d’un nombre présente l’inconvénient d’être très longue. Une base plus élevée est à cet égard préférable. Le choix de la base 10 pourrait paraître naturel, mais malheureusement, convertir un nombre de la base 10 à la base 2 ou inversement n’est pas simple. En revanche, nous allons voir que passer de la base 2 à la base 16 est naturel.
Pour écrire un nombre en base 16, nous avons besoin d’un caractère pour chacun des entiers de 0 à 15 ; on complète donc les chiffres de 0 à 9 par les lettres a, b, c, d, e et f.
Ainsi, $(\text{a})_{16} = 10$, $(\text{b})_{16} = 11$, $(\text{c})_{16} = 12$, $(\text{d})_{16} = 13$, $(\text{e})_{16} = 14$, $(\text{f})_{16} = 15$.
Sachant que $2^4 = 16$, tout nombre écrit en base 2 à l’aide de 4 chiffres s’écrit en base 16 à l’aide d’un seul chiffre :
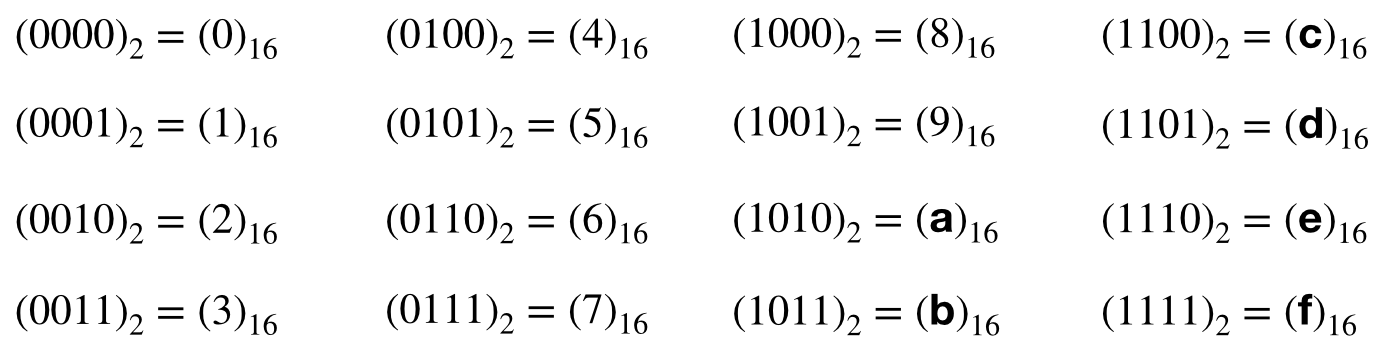
Aussi, pour convertir un nombre quelconque de la base 2 à la base 16, il suffit de regrouper les chiffres qui le composent par paquet de 4 et convertir chacun de ces paquets en un chiffre en base 16.
Par exemple $(1100\,0111\,1110\,1011)_2$ = $(\text{c}7\text{eb})_{16}$.
Un octet (8 bits) est donc représenté par au plus deux caractères hexadécimaux, ce qui explique l’intérêt de cette base (les octets, unité de mémoire, sont partout en informatique).
Exemple : une couleur peut être définie par trois octets représentant ses composantes RVB. Ci-dessous, chaque mot de 3 octets sert aussi à coder la couleur en HTML :
ff0000 00ff00 0000ff
aa00aa 777777 a3850e
07ab98 (code HTML du dernier mot : <font color=#07ab98> 07ab98 </font>)
$256^3 = 16\,777\,216$ couleurs différentes sont ainsi accessibles.
Comme pour les nombres binaires, Python permet d’écrire directement en base 16 si on précède le nombre des caractères 0x.
0xd
13
bin(0xd)
'0b1101'
hex(0b11110111)
'0xf7'
La plus “efficace” des bases est la base ternaire, suivie de près par la base binaire (où la notion d’efficacité est définie dans l’article en lien).
Codage des nombres entiers en machine
Nombres entiers naturels
Les entiers naturels sont essentiellement utilisés pour représenter les adresses en mémoire.
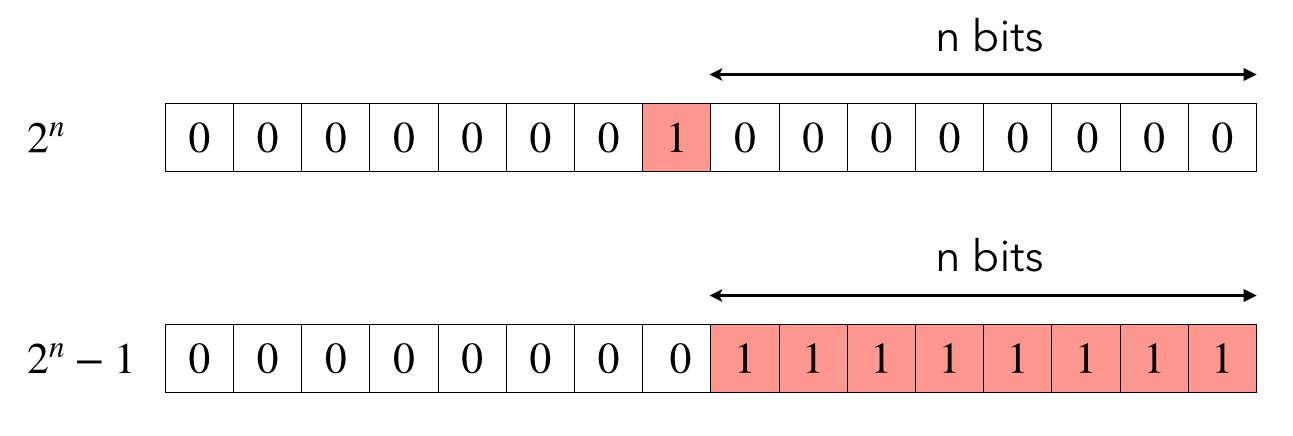
Un mot machine de n bits permet de représenter tous les nombres naturels compris entre 0 et $2^n − 1$. Ainsi, un octet permet de coder les entiers allant de $0 = (00)_{16} = (0000\,0000)_2$ à $255 = (\text{ff})_{16} = (1111\,1111)_2$, et 64 bits (soit 8 octets) tous les nombres allant de $0 = (0000\,0000\,0000\,0000)_{16}$ à $2^{64}−1 = (\text{ffff}\,\text{ffff}\,\text{ffff}\,\text{ffff})_{16}$.
Nombres entiers relatifs
Il faut un bit supplémentaire pour coder le signe. Le premier bit, 0 pour un nombre positif et 1 pour un nombre négatif, est donc réservé.
Ainsi, le plus grand entier relatif représentable sur n bits vaut $2^{n-1}-1$. Pour un processeur 64 bits, cela correspond à $2^{63}-1=(7\text{fff}\,\text{ffff}\,\text{ffff}\,\text{ffff})_{16}$
2**63-1
9223372036854775807
- codage binaire naturel signé
La méthode paraissant la plus simple pour coder les nombres relatifs est alors le codage binaire naturel signé : on place le bit de signe devant la valeur absolue de l’entier codé normalement sur $n-1$ bits. Par exemple, sur 4 bits, 3 est codé par le mot 0011 et -3 par 1011.
Simple, oui, mais cela pose 2 problèmes :
- il y a 2 représentations de 0 (les mots
0000et1000sur 4 bits), - les opérations arithmétiques ne sont pas faciles (l’addition “normale” de 3 et -3 codés ainsi sur 4 bits donnerait
1110, soit -6…).
- complément à 2
La solution qui a été adoptée pour éviter ces problèmes est le complément à 2 :
Ce codage découle du problème posé par l’addition précédente : comment faire pour que l’addition de 2 nombres opposés vaille 0 ? La solution est d’utiliser l’absence du bit $n+1$ dans un codage à $n$ bits. Par exemple, à 4 bits, si on additionne $5$ ($0101$) avec $11$ ($1011$), on obtient $16$ ($\color{red}{1}\color{green}{0000}$) qui devient $0$ ($\color{green}{0000}$) puisqu’il n’y a pas de 5e bit. Il suffit donc d’associer 11 à -5, et de la même façon, 8 à -8, 9 à -7, 10 à -6, 12 à -4, 13 à -3, 14 à -2, et 15 à -1.
De manière générale, pour un codage sur n bits, les $2^{n-1}$ premiers entiers, tous commençants par 0, sont les entiers positifs et on associe les $2^{n-1}$ entiers suivants, commençant par 1, donc négatifs, de façon à ce qu’il complète chaque entier positif à la puissance de 2 supérieure, $2^n$ (d’où “complément à 2”).
Les nombres négatifs sont donc placés au-dessus plutôt qu’en dessous et on peut visualiser ça comme un enroulement sur un cercle des nombres positifs et négatifs.
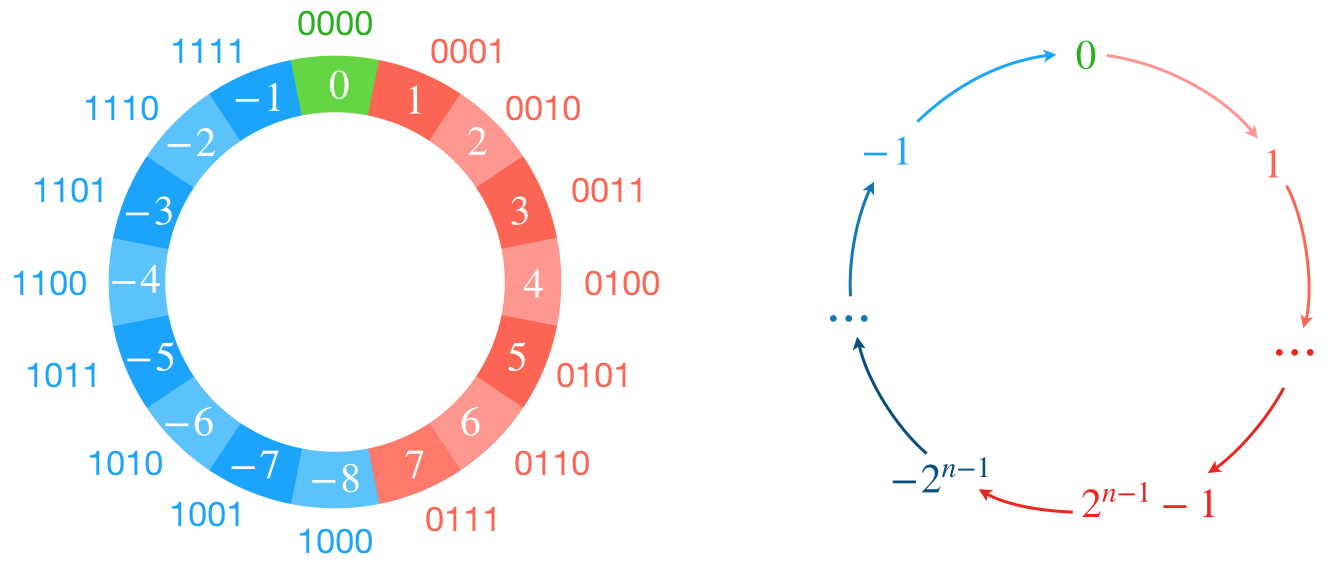
En pratique, si on veut le mot codant -3, il suffit d’inverser chaque bit du codage de 3 et d’ajouter 1 :
$0011 \rightarrow 1100$
$1100+1 = 1101$
donc $-3 \rightarrow 1101$
Dépassement de capacité :
On remarque qu’avec ce type de codage, un dépassement de capacité (ou overflow en anglais) ne lèvera pas d’erreur, mais aboutira à des valeurs aberrantes.
Supposons par exemple que l’on veuille additionner 5 et 7 sur un codage 4 bits. On obtiendra… -4 !
C’est un bug de ce type, un overflow, qui a fait exploser la fusée Ariane 5 lors de son vol inaugural (le vol 501) causant la perte de la fusée et de sa charge utile (4 satellites). Ce bug est un des plus coûteux de l’histoire (370 millions d’euros).
C’est au niveau de la plateforme inertielle (ensemble des capteurs, accéléromètres et gyroscopes, permettant de guider la fusée), héritée de la fusée précédente Ariane 4, que le bug apparut. Plus précisément, c’est le capteur d’accélération horizontale qui fut débordé pendant sa phase de calibrage (lors des premières 40 s du vol). Codée sur 8 bits, la valeur d’accélération maximum représentable était donc de $2^7-1=127$, ce qui était suffisant pour Ariane 4 (valeur max : 64). Mais plus puissante et avec une trajectoire de décollage différente, Ariane 5 engendre des accélérations horizontales qui peuvent être jusqu’à 5 fois plus fortes pendant la phase de décollage (valeur max : 300). Cela aboutit à une valeur absurde que le guidage essaya de compenser… boom.
Et comble de la frustration : ce calibrage en début de vol était devenu inutile pour Ariane 5.
Qu’en est-il de Python ?
Contrairement à la plupart des langages, Python n’alloue pas de taille à priori aux entiers. Par conséquent, ils peuvent dépasser la taille maximale adressable par le processeur et sont donc de précision arbitraire, la seule limite étant la taille totale de la RAM.
2**200
1606938044258990275541962092341162602522202993782792835301376
Si cela facilité pas mal les opérations arithmétiques sur les grands nombres, cela complique l’étude de la complexité, car si un entier prend plusieurs mots mémoires, la plupart de ses manipulations ne sont plus des étapes élémentaires.
D’autre part, certain package très utilisé, et particulièrement NumPy, utilisent des entiers de précision fixée.
import numpy as np
a = np.array(2**63-1)
a.dtype
dtype('int64')
Ajouter 1 à a va causer un overflow sans lever d’erreurs :
b = a+1
b
-9223372036854775808
a + b
-1
Exemple :
C’est bien en utilisant Numpy qu’on a été confronté au TP7 au problème du dépassement de capacité. Chaque couleur d’une image étant codée sur un octet dans un tableau Numpy, certaines opérations pouvaient provoquer un dépassement et donner des résultats bizarres.

Revenons sur la conversion d’une image couleur avec une profondeur de 24 bits (un octet par couleur) en une image 6 bits (2 bits pour chaque couleur).
Avec cette méthode, on a bien une image de 6 bits de profondeur mais elle paraît assombrie par rapport à l’originale.
L’idée est alors de décaler toutes les valeurs de $2^5$, mais cela provoque un dépassement de capacité !
Pour corriger cela, on peut convertir le tableau en 16 bits avant de lui ajouter $2^5$ puis le reconvertir à la fin en 8 bits :
imageconvertie = (imageoriginale.astype(np.uint16) // 2**6 * 2**6 + 2**5).astype(np.uint8)

Codage des nombres réels en machine
Écriture finie ou infinie
Un nombre décimal $x$ est un nombre pouvant s’écrire sous la forme $\frac{x}{10^n}$. Son développement décimal s’obtient en décomposant $x$ sur les puissances de 10 positives et négatives d’exposants allant au maximum jusqu’à -n : $\frac{5}{8}=0,625=\frac{625}{10^3} = \frac{6}{10^1}+ \frac{2}{10^2} + \frac{5}{10^3}$. Mais la plupart des nombres ne possède pas un développement décimal fini ($\frac{1}{3}=0,33333\cdots$ par exemple).
L’équivalent binaire des nombres décimaux correspond aux nombres dyadiques. Ainsi, $\frac{5}{8}=\frac{5}{2^3}$ est un nombre dyadique et son développement dyadique s’écrit : $\frac{5}{8}=\frac{1\times 2^2+0\times 2^1+1\times 2^0}{8}=\frac{1}{2^1}+\frac{0}{2^2}+\frac{1}{2^3}=(0,101)_2$
Comme pour les décimaux, la plupart des nombres ne possèdent pas un développement dyadique fini, mais cela ne correspond pas aux mêmes nombres !
C’est le cas par exemple de $0,1$ : $\frac{1}{10} = (0,0001\,1001\,1001\,1001\cdots)_2$.
La représentation de $0,1$ sera donc nécessairement tronquée par la machine :
0.1**2
0.010000000000000002
0.1**2 == 0.01
False
Conclusion : il faut réserver les tests d’égalité aux entiers ! Pour les flottants, il faut se restreindre à tester des inégalités.
Au lieu de vérifier l’égalité entre deux flottants, on se borne donc à vérifier qu’ils sont suffisamment proches en se fixant un écart minimal faible ($\varepsilon = 10^{-10}$ par exemple).
Exemple :
abs(0.1**2 - 0.01) < 1e-10
True
Écriture binaire de la partie fractionnaire d’un nombre
Pour convertir en binaire la partie fractionnaire d’un nombre en base 10, rien de plus simple :
- on multiplie la partie décimale par 2,
- si ça dépasse 1, on retire 1 au nombre obtenu, et on ajoute 1 à l’écriture binaire
- sinon, on garde la nombre obtenu, et on ajoute 0 à l’écriture binaire
- puis on recommence en multipliant par 2 le nombre obtenu précédemment.
Exemple avec 0,625 :
L’écriture binaire commence par “0,"
$0,625\times 2 = \textcolor{red}{1},25$ $\rightarrow$ “$0,\color{red}1$” (on garde $1,25-1 = 0,25$)
$0,25\times 2 = \textcolor{blue}{0},5$ $\rightarrow$ “$0,1\color{blue}0$"
$0,5\times 2 = \textcolor{red}1$ et comme $1-1=0$, on a fini $\rightarrow$ “$0,10\color{red}1$”
Exemple avec 0,1 :
$0,1\times 2 = \textcolor{blue}{0},2$ $\rightarrow$ “$0,\color{blue}0$"
$0,2\times 2 = \textcolor{blue}{0},4$ $\rightarrow$ “$0,0\color{blue}0$"
$0,4\times 2 = \textcolor{blue}{0},8$ $\rightarrow$ “$0,00\color{blue}0$"
$0,8\times 2 = \textcolor{red}{1},6$ $\rightarrow$ “$0,000\color{red}1$” (et on garde $1,6-1 = 0,6$)
$0,6\times 2 = \textcolor{red}{1},2$ $\rightarrow$ “$0,0001\color{red}1$” (on garde $1,2-1 = 0,2$)
$0,2\times 2 = \textcolor{blue}{0},4$ $\rightarrow$ “$0,00011\color{blue}0$"
$0,4\times 2 = \textcolor{blue}{0},8$ $\rightarrow$ “$0,000110\color{blue}0$"
…
Écrire une fonction
fractbin(n: float, c: int) -> :strqui donne l’écriture fractionnaire en binaire d’un nombre décimalnaveccchiffres après la virgule.
Nombres en virgule flottante
Nous connaissons la notation scientifique qui normalise tous les nombres décimaux avec une mantisse comprise entre 1 et 9,999… et une puissance de dix restituant la grandeur du nombre.
Les nombres en virgule flottante (ou au format flottant) peuvent être vus comme l’équivalent informatique de la notation scientifique.
La notation flottante comprend trois composantes :
- le signe s,
- la mantisse m,
- l’exposant e de la puissance de b.
Un nombre $x$ s’écrit donc $x=s\times m\times b^e$ où $b$ est la base.
En faisant varier l’exposant, on fait « flotter » la virgule.
Le format flottant est le format privilégié pour représenter les nombres décimaux en machine (la base est alors 2 bien sûr).
Norme IEEE-754
La norme elle-même n’est pas à connaître, mais son principe permet de comprendre comment les mots machines correspondant aux flottants sont construits.
Cette norme est actuellement le standard pour la représentation des nombres à virgule flottante en binaire.
Pour une architecture 64 bits, le signe est codé sur 1 bit, l’exposant sur 11 et la mantisse sur 52. Le format est alors dit double précision pour le distinguer du simple précision stocké sur 32 bits.

Comme le premier chiffre significatif d’un nombre binaire est nécessairement 1, ce 1 n’est pas inclus dans les 52 bits de la mantisse. Les 52 bits permettent donc 53 bits de précision grâce à ce bit caché. On dit alors que le flottant est normalisé.
Exemple : comment est représenté le nombre décimal $13256,625$ ?
$13256,625 = (11001111001000,101)_2 = 1,1001111001000101\times 2^{13}$
Donc l’exposant vaut 13, et comme on l’a dit, on omet le premier 1 dans la mantisse qui s’écrit donc :
$\color{blue}1001111001000101000000000000000000000000000000000000$ (les 16 bits après le premier 1 de l’écriture binaire de $13256,625$ suivis de 36 zéros).
L’exposant est représenté avec un décalage : on lui ajoute $2^{10}-1=1023$.
Cela permet de stocker des exposants allant de $-1022$ à $1023$ sur des valeurs toutes positives allant de $1$ à $2046$.
Dans notre cas, l’exposant est représenté avec la valeur $13+1023=1036=10000001100$
Au final, la représentation au format flottant 64 bits normalisé de $13256,625$ est :
$\color{teal}{0}\;\color{magenta}{10000001100}\;\color{blue}{1001111001000101000000000000000000000000000000000000}$
Elle est exacte.
Par contre, la représentation de $0,1$ est, elle, tronquée :
$\color{teal}{0}\;\color{magenta}{01111111011}\;\color{blue}{1001100110011001100110011001100110011001100110011010}$
En décimal, ce nombre correspond à $0,100000000000000005551115123126$.
Les soucis des flottants
En général, les 53 bits (en incluant le bit caché) permettent 15 chiffres significatifs en décimal ($\log_{10} 2^{53} = 15,95$).
Tout calcul impliquant un nombre de chiffres plus grands sera sujet à une erreur d’arrondi.
La limite supérieure de l’erreur d’approximation relative causée par l’arrondi est appelée epsilon de la machine $\varepsilon$.
Pour Python :
import sys
eps = sys.float_info.epsilon
eps
2.220446049250313e-16
Cette valeur est logiquement $2^{-52}$, la dernière position de la mantisse.
Conséquence de ces arrondis : lors de l’addition de deux nombres à l’écart relatif très important, il peut y avoir absorption du petit par le grand !
L’addition de flottants n’est plus associative.
(1 + 2.**53) - 2.**53
0.0
1 + (2**53 - 2**53)
1
Explication : $1+2^{53} = (1, \underbrace{000\cdots000}_\text{52 zéros}\,\color{red}{1}\color{black}{)_2 \times 2^{53}} \Rightarrow$ Le dernier 1 se voit tronqué.
Et c’est pour ça que le code suivant termine !
x = 1.0
p = 0
while x != x+1:
x *= 2
p += 1
print(x)
print(p)
9007199254740992.0
53
De plus, la multiplication de flottants n’est en général pas distributive.
a, b, c = 100, 0.1, 0.2
a*b + a*c
30.0
a*(b+c)
30.000000000000004
Beaucoup de calculs en flottants entraînent la perte de chiffres significatifs.
Les cas les plus spectaculaires intervenant lorsqu’on soustrait deux nombres très proches.
Prenons, pour simplifier, l’exemple de flottants décimaux dont la mantisse s’écrit sur 6 bits et représentons le calcul dont la forme exacte est :
$1,2345432 - 1,23451 = 0,0000332$
Notre système hypothétique est obligé de tronquer le premier terme $1,2345432 \rightarrow 1,23454$.
Le résultat de la soustraction donne alors :
$1,23454 - 1,23451 = 0,00003$
On n’a plus qu’un seul chiffre significatif alors que le résultat exact avec ses 3 chiffres significatifs pouvait très bien être représenté par notre système à mantisse de 6 bits.
On parle alors de catastrophic cancellation.
Même si les 15 chiffres significatifs des flottants double précision semblent beaucoup, des opérations répétées entraînent une cascade d’arrondis qui peuvent aboutir à des résultats dramatiques comme le montre l’exemple du missile patriot du TP.
Une autre conséquence de la manière dont les flottants sont gérés est l’existence de valeur minimale et maximale stockable.
Les calculs bayésiens, par exemple, requièrent de fréquentes multiplications entre petites probabilités. Mais en dessous d’une certaine valeur, un soupassement de capacité ou underflow amène le programme à afficher zéro.
P = 1
for i in range(1,101):
if (i<6 or P<1e-306):
print(P)
elif i == 10:
print('...')
P *= 5e-4
1
0.0005
2.5e-07
1.25e-10
6.250000000000001e-14
...
1.0097419586828971e-307
5.0487097934146e-311
2.5243548965e-314
1.2621776e-317
6.31e-321
5e-324
0.0
On voit que la précision est progressivement abaissée avec l’affichage de nombres dits subnormaux (ce processus est appelé “gradual underflow”) avant l’affichage de zéro.\
Le plus petit nombre qui peut être représenté avec une précision complète est :
sys.float_info.min
2.2250738585072014e-308
De l’autre côté, on a la possibilité d’un dépassement de capacité ou overflow. Le plus grand nombre affichable est :
sys.float_info.max
1.7976931348623157e+308