TP 10 : les graphes

TP10 : les graphes

Cliquez sur cette invitation pour récupérer le repository du TP.

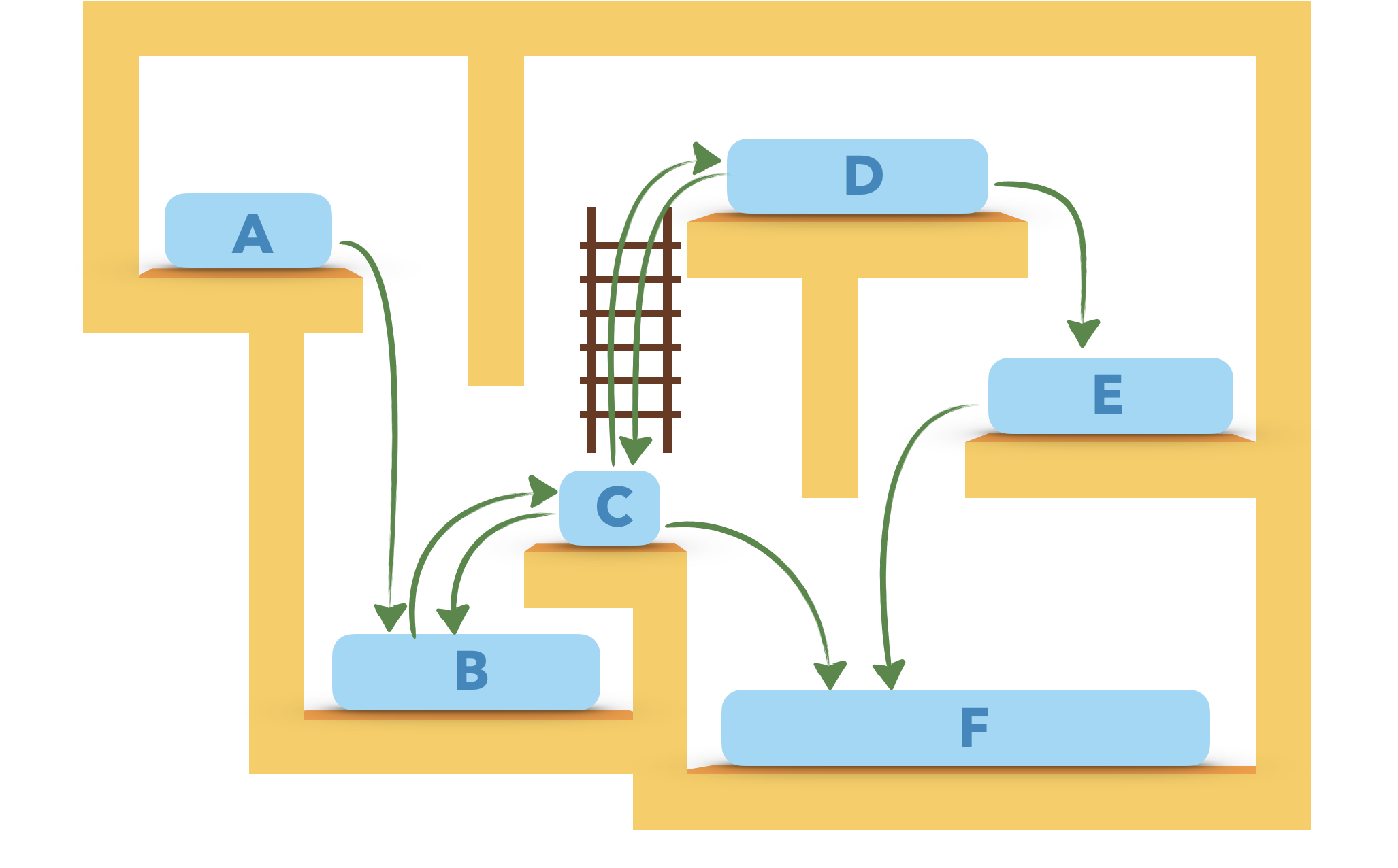
Le dessin ci-dessus peut se représenter par (choisir la bonne réponse) :

a : un graphe orienté

b : un graphe non orienté

Correction (cliquer pour afficher)

Un graphe orienté.

Le degré du sommet C vaut :

a : 2

b : 3

c : 5

Correction (cliquer pour afficher)

5

Le distance de F à C vaut :

a : 1

b : 3

c : $\infty$

Correction (cliquer pour afficher)

Comme il n'y a pas de chemin allant de F à C, la distance est dite par convention infinie.

En transformant les arcs en arêtes, quel serait le diamètre du graphe ?

a : 4

b : 5

c : $\infty$

Correction (cliquer pour afficher)

Le diamètre d'un graphe est la plus grande des distances entre deux sommets.
Ici, il vaut 4.

Listes et matrices d’adjacence

Construire le graphe G_la correspondant au dessin du haut sous la forme d’une liste d’adjacence en utilisant un dictionnaire (sur le modèle du cours).
Les sommets devront s’appeler "A","B","C","D","E" et "F".

Correction (cliquer pour afficher)

G_la = {"A":["B"],
        "B":["C"],
        "C":["B","D","F"],
        "D":["C","E"],
        "E":["F"],
        "F":[]}

Construire maintenant le graphe G_ma correspondant au dessin ci-dessus sous la forme d’une matrice d’adjacence (en suivant le modèle donné dans le cours).

Correction (cliquer pour afficher)

G_ma = [[0,1,0,0,0,0],
        [0,0,1,0,0,0],
        [0,1,0,1,0,1],
        [0,0,1,0,1,0],
        [0,0,0,0,0,1],
        [0,0,0,0,0,0]]

Manipulation d’un graphe

Ajouter un sommet à un graphe

Construire une fonction qui ajoute un sommet S à un graphe G orienté. Le graphe G est représenté par une liste d’adjacence et on donne en argument de la fonction la liste des prédécesseurs et des successeurs du sommet S ($Pred(S)$ et $Succ(S)$).

def ajouteSommet(G,S,pred,succ):
    """
    ajouteSommet(G: dict,S: str,pred: list,succ: list) -> G: dict
    préconditions: G est un graphe dont certains des sommets font partie de la liste pred et certains de la liste succ.
    S est le nom d'un sommet n'appartenenat pas à G.
    G est modélisé par une liste d'adjacence utilisant un dictionnaire.
    pred et succ sont les listes des prédécesseurs et des successeurs de S.
    postcondition: la fonction retourne le graphe mis à jour (muté) avec le sommet S ajouté.
    """
    # VOTRE CODE

Correction (cliquer pour afficher)

def ajouteSommet(G,S,pred,succ):
    G[S] = succ
    for sp in pred:
        G[sp].append(S)
    return G

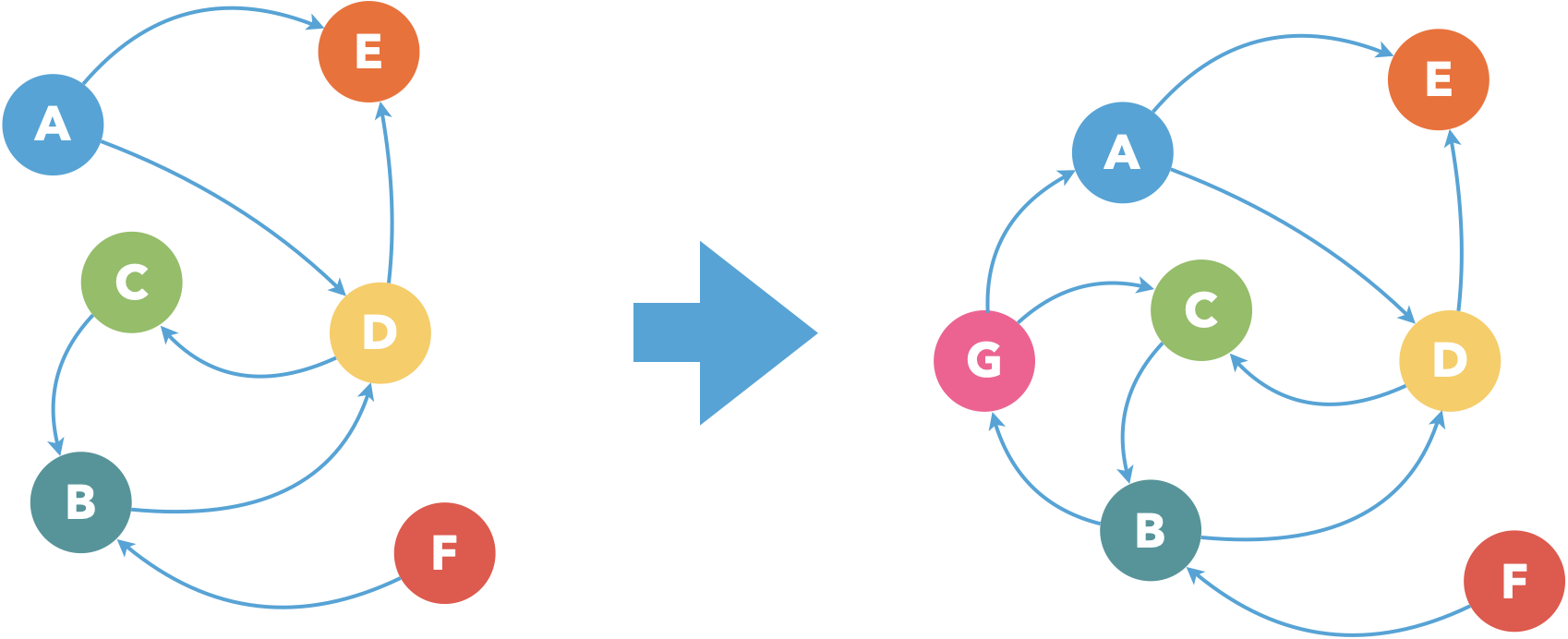
Le graphe de gauche est modélisé ci-dessous par une liste d’adjacence :

Graphe = {'A' : ['E','D'],
          'B' : ['D'],
          'C' : ['B'],
          'D' : ['C','E'],
          'E' : [],
          'F' : ['B']}

On souhaite lui ajouter le sommet 'G'.

Compléter au préalable les listes Pred et Succ contenant les prédécesseurs et les successeurs de 'G'.

Pred = []
Succ = []

Correction (cliquer pour afficher)

Pred = ['B']
Succ = ['A','C']

Testez ensuite votre fonction ajouteSommet pour vérifier que le graphe est modifié comme souhaité.

Correction (cliquer pour afficher)

ajouteSommet(Graphe,'G',Pred,Succ) donne alors :

{'A': ['E', 'D'],
'B': ['D', 'G'],
'C': ['B'],
'D': ['C', 'E'],
'E': [],
'F': ['B'],
'G': ['A', 'C']}

Retirer un sommet à un graphe

On souhaite maintenant construire la fonction retireSommet permettant de retirer un sommet d’un graphe.
Elle prend en argument le graphe et un sommet du graphe.
Vous utiliserez un assert pour vous assurer que le sommet passé en argument appartient bien augraphe.

def retireSommet(G,S):
    """
    retireSommet(G: dict,S: str) -> G: dict
    préconditions: G est un graphe et S est un de ses sommets.
    G est modélisé par une liste d'adjacence utilisant un dictionnaire
    postcondition: la fonction retourne le graphe mis à jour (muté) avec le sommet S en moins
    """
    # VOTRE CODE

Correction (cliquer pour afficher)

def retireSommet(G,S):
    assert S in G
    del G[S]
    for liste in G.values():
        if S in liste:
            liste.remove(S)
    return G

Reprenons le graphe précédent avant l’ajout du sommet 'G'.

Graphe = {'A' : ['E','D'],
          'B' : ['D'],
          'C' : ['B'],
          'D' : ['C','E'],
          'E' : [],
          'F' : ['B']}

Testez ensuite votre fonction retireSommet pour vérifier que le graphe est modifié comme souhaité.

Utilisation d’un module pour visualiser

import networkx as nx
from IPython.display import Image
import pandas as pd

Construisons la matrice d’adjacence d’un graphe non-orienté complet.

matrice = [[0, 3, 2, 2, 1, 6, 4, 2, 6, 5],
           [3, 0, 6, 6, 4, 3, 6, 5, 4, 5],
           [2, 6, 0, 6, 2, 3, 1, 1, 2, 6],
           [2, 6, 6, 0, 4, 3, 2, 2, 4, 6],
           [1, 4, 2, 4, 0, 3, 6, 1, 6, 2],
           [6, 3, 3, 3, 3, 0, 6, 2, 6, 6],
           [4, 6, 1, 2, 6, 6, 0, 4, 2, 5],
           [2, 5, 1, 2, 1, 2, 4, 0, 4, 2],
           [6, 4, 2, 4, 6, 6, 2, 4, 0, 2],
           [5, 5, 6, 6, 2, 6, 5, 2, 2, 0]]

Construisez à votre tour une matrice $10\times 10$ M semblable à la précédente en tirant chaque élément au hasard parmi la liste [1,2,3,4,5,6] grâce à la fonction choice du module random (choice(L) retourne un des éléments de L choisi au hasard).
Cette matrice devra n’avoir que des 0 dans sa diagonale et être symétrique.
Attention: le nom de la matrice doit être M.

from random import choice

n = 10 # nombre de sommets

# VOTRE CODE

Correction (cliquer pour afficher)

M = [[choice([1,2,3,4,5,6]) for i in range(n)] for j in range(n)]
for i in range(n):
    M[i][i] = 0
    for j in range(i):
        M[j][i] = M[i][j]

Si vous avez réussi à construire M vous pourrez utilisez votre matrice par la suite.

On transforme ensuite la matrice en dataframe pandas (pandas est un module de gestion de données très riche déjà utilisé dans le tp3 et un dataframe est un tableau à deux dimensions) qui sera reconnue par networkx et on lui ajoute des lettres en en-tête de ligne et de colonne pour nommer les sommets.

abc = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
labels = list(abc[:n])
M_df = pd.DataFrame(matrice, index=labels, columns=labels)
print(M_df)

	A	B	C	D	E	F	G	H	I	J
A	0	3	2	2	1	6	4	2	6	5
B	3	0	6	6	4	3	6	5	4	5
C	2	6	0	6	2	3	1	1	2	6
D	2	6	6	0	4	3	2	2	4	6
E	1	4	2	4	0	3	6	1	6	2
F	6	3	3	3	3	0	6	2	6	6
G	4	6	1	2	6	6	0	4	2	5
H	2	5	1	2	1	2	4	0	4	2
I	6	4	2	4	6	6	2	4	0	2
J	5	5	6	6	2	6	5	2	2	0

G_complet = nx.from_pandas_adjacency(M_df) # obtention du graphe networkx à partir de la dataframe

weights = [G_complet[u][v]['weight']*3 for u,v in G_complet.edges()] # liste des poids (*3)

# Tracé
options = {"font_size": 20,
           "font_weight":"bold",
           "node_size": 1000,
           "node_color": "#34A5DA",
           "edge_color": weights,  # couleur en fonction des poids
           "width": weights,       # épaisseur des arêtes en fonction des poids
           "edge_cmap": plt.cm.Set3,
           "with_labels": True,
           "font_color": "white",
           "linewidths": 5,
          }

pos = nx.shell_layout(G_complet)
fig = plt.figure(figsize=(12, 12))
nx.draw(G_complet,pos=pos,**options)
labels = nx.get_edge_attributes(G_complet,'weight')
nx.draw_networkx_edge_labels(G_complet, pos=pos,edge_labels=labels)
plt.show()

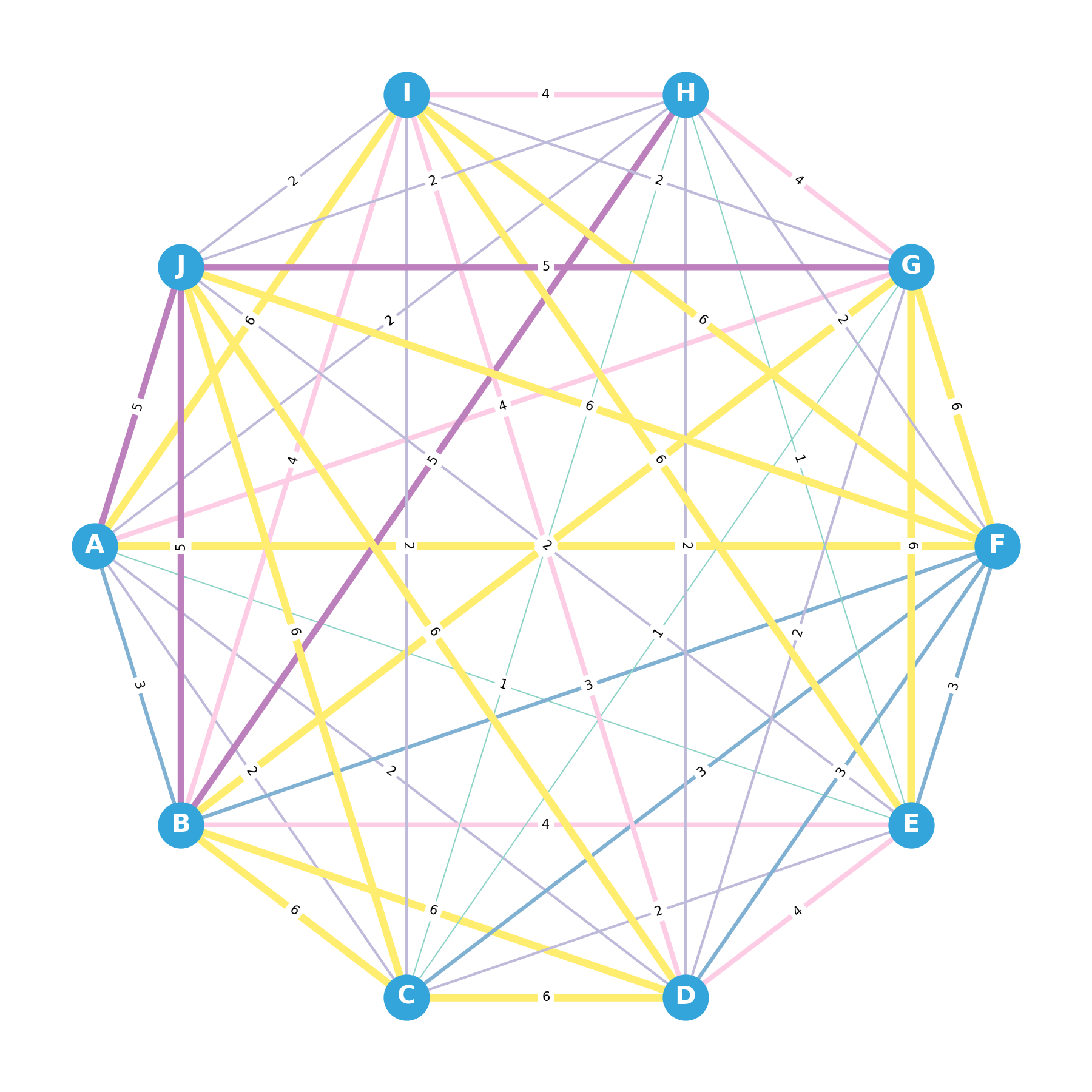
Transformez la matrice matrice en une liste d’adjacence G_la n’utilisant que des dictionnaires.
G_la devra ressembler à :

{'A': {'B': 3, 'C': 2, 'D': 2, 'E': 1, 'F': 6, 'G': 4, 'H': 2, 'I': 6, 'J': 5},
 'B': {'A': 3, 'C': 6, 'D': 6, 'E': 4, 'F': 3, 'G': 6, 'H': 5, 'I': 4, 'J': 5},
 'C': {'A': 2, 'B': 6, 'D': 6, 'E': 2, 'F': 3, 'G': 1, 'H': 1, 'I': 2, 'J': 6},
 'D': {'A': 2, 'B': 6, 'C': 6, 'E': 4, 'F': 3, 'G': 2, 'H': 2, 'I': 4, 'J': 6},
 'E': {'A': 1, 'B': 4, 'C': 2, 'D': 4, 'F': 3, 'G': 6, 'H': 1, 'I': 6, 'J': 2},
 'F': {'A': 6, 'B': 3, 'C': 3, 'D': 3, 'E': 3, 'G': 6, 'H': 2, 'I': 6, 'J': 6},
 'G': {'A': 4, 'B': 6, 'C': 1, 'D': 2, 'E': 6, 'F': 6, 'H': 4, 'I': 2, 'J': 5},
 'H': {'A': 2, 'B': 5, 'C': 1, 'D': 2, 'E': 1, 'F': 2, 'G': 4, 'I': 4, 'J': 2},
 'I': {'A': 6, 'B': 4, 'C': 2, 'D': 4, 'E': 6, 'F': 6, 'G': 2, 'H': 4, 'J': 2},
 'J': {'A': 5, 'B': 5, 'C': 6, 'D': 6, 'E': 2, 'F': 6, 'G': 5, 'H': 2, 'I': 2}}

Correction (cliquer pour afficher)

G_la = {}
for i in range(n):
    D = {}
    for j in range(n):
        if matrice[i][j] != 0:
            D[abc[j]] = matrice[i][j]
    G_la[abc[i]] = D

Une application concrète des graphes : l’arbre couvrant minimal

Supposons que chaque sommet du graphe précédent représente les nœuds d’un réseau que l’on souhaite relier à moindre coût. Ces sommets peuvent être des villes que l’on veut relier électriquement, des champs à irriguer, des serveurs à relier, etc. Les différents poids des arêtes matérialisent la difficulté ou le coût de la liaison entre les deux sommets.
Comment trouver facilement le moyen de relier tout le monde en minimisant les coûts ? Il faut trouver un arbre couvrant minimal du graphe.

Un arbre couvrant est un arbre (graphe sans cycle) qui rejoint tous les sommets d’un graphe connexe.
Un arbre couvrant minimal est un arbre couvrant dont la somme des poids des arêtes est minimale.

Chercher une solution par force brute devient rapidement impossible quand le nombre de sommets du graphe augmente. La formule de Cayley nous dit qu’il y aura $n^{n-2}$ arbres couvrants d’un graphe complet connexe comportant n sommets (avec seulement 100 sommets, cela fait plus de possibilités que le nombre d’atomes dans l’univers).

Quelle serait donc le type de complexité d’une exploration par force brute de tous les arbres couvrants ?

a : logarithmique en n

b : polynomiale en n

c : exponentielle en n

Correction (cliquer pour afficher)

Pire qu'exponentielle en fait, mais on classe généralement tout ça ($n!$, $,n^n$, etc.) sous l'étiquette exponentielle car c'est quoiqu'il arrive trop lent.

Grâce à l’algorithme de Prim, on peut trouver un arbre couvrant minimal d’un graphe connexe pondéré en temps raisonable !

Mais commençons d’abord par construire une fonction qui vérifie si un graphe est connexe ou non.
Pour cela, on va utiliser l’algorithme de parcours en profondeur (Deep-First Search) sur le graphe à tester en partant d’un sommet quelconque et vérifier que tous les sommets sont visités.

from collections import deque

def parcours_profondeur(G,depart):
    pile = deque()
    pile.append(depart)
    Vus = []
    while pile :
        sommet = pile.pop()
        if not sommet in Vus :
            pile += G[sommet]
            Vus.append(sommet)
    return Vus

Construisez la fonction verifConnexe qui vérifie si un graphe est connexe ou non.
Vous utiliserez la fonction parcours_profondeur dans votre code.
Vous pourrez ensuite tester ci-dessous si votre fonction fait le travail sur les deux listes d’adjacence G_la et Gt_nc.
Dans le premier cas, le graphe est évidemment connexe, et on a construit le deuxième pour qu’il ne le soit pas.

def verifConnexe(G):
    """
    verifConnexe(G: dict) -> bool
    précondition: G est un graphe sous la forme d'une liste d'adjacence représentée par un dictionnaire comme ci-dessus
    postcondition: la fonction retourne True si le graphe est connexe, False sinon
    """
    # VOTRE CODE

Correction (cliquer pour afficher)

def verifConnexe(G):
    depart = list(G.keys())[0]
    Sommets = parcours_profondeur(G,depart)
    if len(Sommets) == len(G):
        return True
    else:
        return False

# Construction d'un graphe G_nc non connexe
G_nc = nx.Graph()
G_nc.add_nodes_from([i for i in range(1,9)])
color_map = ['red' if node <=4 else 'green' for node in G_nc]
G_nc.add_edges_from([(1, 2), (1, 3),(2,4),(1,4),(5,7),(6,7),(5,8),(7,8)])
posi = nx.kamada_kawai_layout(G_nc)
options = {"node_size": 200,
           "node_color": color_map,
           "edge_color": color_map,
           "linewidths": 1,
           "width": 1,
           "with_labels": False,
          }
G_nc_la = nx.to_dict_of_dicts(G_nc)
nx.draw(G_nc,posi,**options)

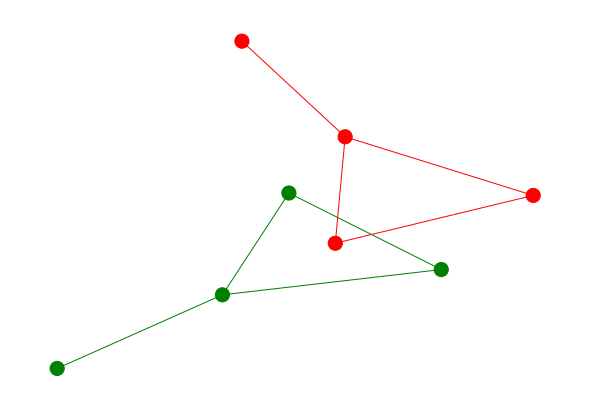
print('G_la est connexe :',verifConnexe(G_la))
print('G_nc_la est connexe :',verifConnexe(G_nc_la))

G_la est connexe : True
G_nc_la est connexe : False

Implémentons maintenant une version lente (quadratique) de l’algorithme de Prim.

Comme Dijkstra, Prim est un algorithme glouton. À chaque itération, il se jette sur l’arête de poids le plus faible permettant de traverser la frontière entre l’ensemble des sommets déjà inspectés et l’ensemble des autres. Une fois l’arête choisie, on ajoute le sommet non inspecté qu’elle relie à l’ensemble des sommets inspectés.

Intégrez à l’algorithme ci-dessous une assertion testant si le graphe donné en argumant est bien connexe et ajoutez une variable cout à l’algorithme qui enregistre le coût de l’arbre final retourné et qui devra elle aussi être retournée.
La sortie doit donc devenir : return A, cout

def Prim(G):
    """
    Prim(G : dict) -> A : liste de tuples , cout : nombre
    G est donné sous la forme d'une liste d'adjacence implémenté par un dictionnaire
    A est une liste d'arêtes représentées par un tuple (A,B) où A et B sont les deux sommets délimitant l'arête
    cout est le coût de l'arbre A (somme des pondération des arêtes constituant A)
    postcondition : A doit être un arbre couvrant minimal
    """
    inf = float('inf')
    NX = list(G.keys()) # un dictionnaire n'est pas ordonné donc pas indiçable d'où la transformation en liste
    S0 = NX[0] 
    X = [S0]
    NX.remove(S0)
    A = []
    while NX != []:
        # invariant : A est un arbre couvrant minimal de X
        Min = inf
        for S1 in X:
            for S2 in NX:
                if G[S1].get(S2,inf) < Min: # get(clé,v0) renvoie la valeur liée à la clé si la clé existe et v0 sinon (permet d'éviter les "key error")
                    Min = G[S1][S2] # là, on sait que S2 est bien un voisin de S1
                    Fmin = S2
                    Dmin = S1
        X.append(Fmin)
        NX.remove(Fmin)
        A.append((Dmin,Fmin))
    return A

Correction (cliquer pour afficher)

def Prim(G):
    assert verifConnexe(G) # assertion demandée
    inf = float('inf')
    NX = list(G.keys())
    S0 = NX[0]
    X = [S0]
    NX.remove(S0)
    A = []
    cout = 0 # initialisation du cout
    while NX != []:
        Min = inf
        for S1 in X:
            for S2 in NX:
                if G[S1].get(S2,inf) < Min:
                    Min = G[S1][S2]
                    Fmin = S2
                    Dmin = S1
        X.append(Fmin)
        NX.remove(Fmin)
        A.append((Dmin,Fmin))
        cout += Min # incrémentation du cout
    return A,cout

Traçons maintenant l’arbre couvrant minimal trouvé par Prim.

A,cout = Prim(G_la)
H = nx.Graph()
for S in abc[:n]:
    H.add_node(S)
for S1,S2 in A:
    H.add_edge(S1,S2,weight=10)
F = nx.compose(G_complet,H)

weights = [5 if F[u][v]['weight']==10 else 0 for u,v in F.edges()]

options = {"font_size": 20,
           "font_weight":"bold",
           "node_size": 1000,
           "node_color": "#34A5DA",
           "edge_color": weights,
           "width": weights,
           "edge_cmap": plt.cm.bwr,
           "with_labels": True,
           "font_color": "white",
           "linewidths": 1,
          }

fig = plt.figure(figsize=(12, 12))
nx.draw(F,pos=pos,**options)
plt.show()
print(f"Coût de l'arbre : {cout}")

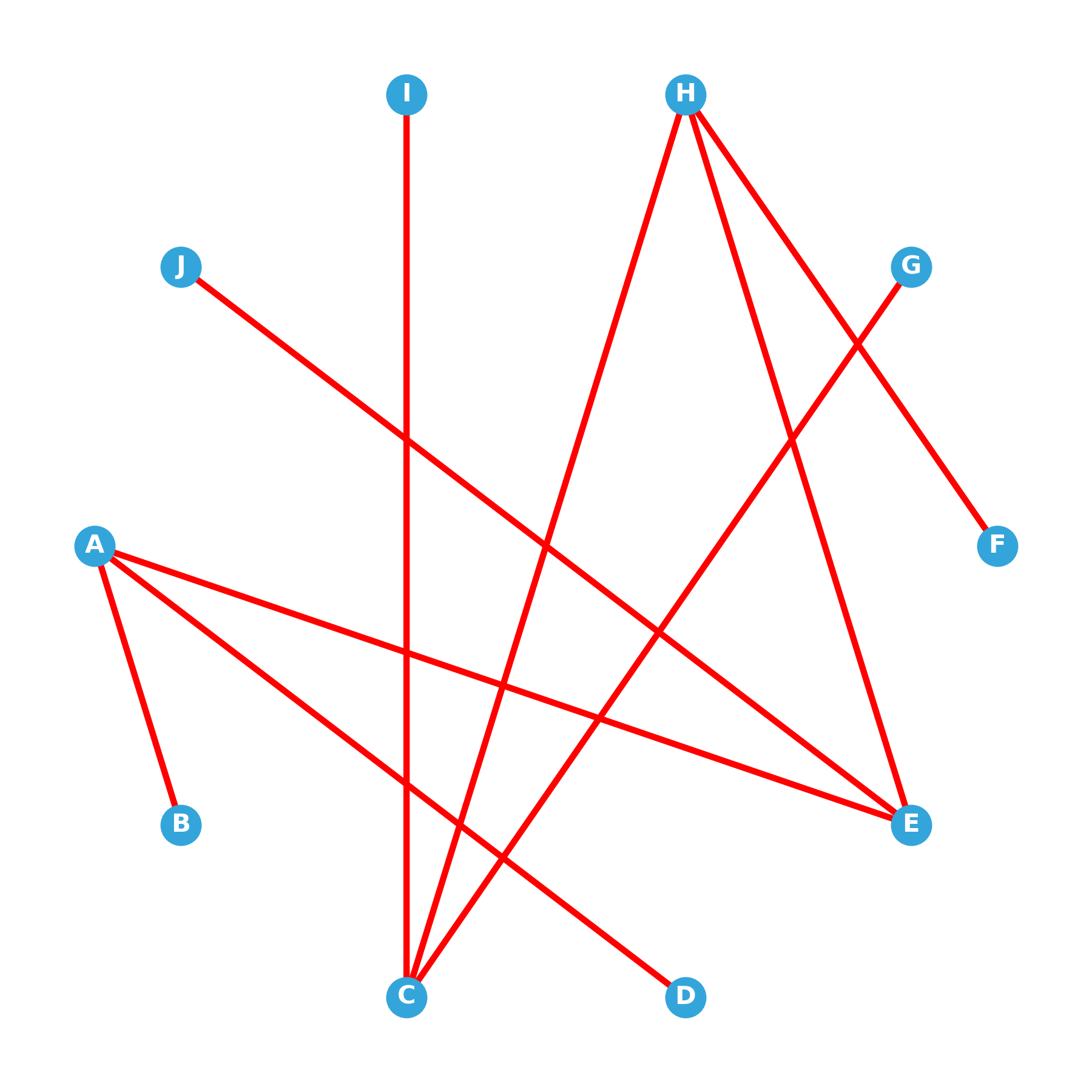
Coût de l'arbre : 15

Et voilà ! En deux coups de cuillère à pot, on a trouvé un arbre couvrant minimal sans s’infliger l’inspection systématique des $10^8$ arbres couvrants possibles…

Lien entre structures de données et graphes, exemple du tas

Le tas est une structure de données permettant d’implémenter une file de priorité dont le rôle est d’obtenir rapidement le plus petit élément d’un ensemble.
On peut se représenter un tas par un arbre binaire presque complet ordonné.

Pour implémenter un tas, on retranscrit l’arbre binaire sous la forme d’une liste.

En vous aidant de la vidéo ci-dessus, choisir parmi les listes suivantes celle qui peut représenter un tas :

a : [3,5,8,5,13,7,9,6,12,15,18,11,12,10]
b : [3,5,8,5,13,11,11,6,12,15,18,11,11,12,10]
c : [3,5,8,5,13,11,9,6,12,15,18,11,12]

Correction (cliquer pour afficher)

a : le parent à la position 3 a un enfant plus petit que lui (position 6)

b : le parent à la position 7 a un enfant plus petit que lui (position 15)

c : tout va bien

Construire une fonction plusPetitEnfant qui retourne la position du petit enfant d’un élément dans le tas.
La fonction prend en argument le tas (représenté sous la forme d’une liste) et la position du parent.
La fonction retourne la position du plus petit enfant.
Si l’élément n’a pas d’enfant, la fonction retourne None.
Attention : les positions dans le tas vont de 1 à n (et non de 0 à n-1) où n est le nombre d’éléments dans le tas.

def plusPetitEnfant(tas,position):
    """ 
    plusPetitEnfant(tas: list, position: int) -> int ou Nonetype
    """
    # VOTRE CODE

Si Tas = [3,7,8,8,7,12,9,9,8,8,8,13] et pos = 3, alors plusPetitEnfant(Tas,pos) doit retourner 7 (car à la position 3, on trouve 8 dont les deux enfants 12 et 9 sont aux positions 6 et 7).

Correction (cliquer pour afficher)

def plusPetitEnfant(tas,position):
    n = len(tas)
    if 2*position > n:
        return None
    elif 2*position == n:
        return 2*position
    else:
        if tas[2*position-1] <= tas[2*position]:
            return 2*position
        else:
            return 2*position+1

Construire les fonctions insert et extractMin (pour cette dernière, pensez à utiliser plusPetitEnfant).
On supposera que le tas ne contient que des entiers.

def insert(tas,x):
    """
    insert(tas: list , x: int) -> Nonetype
    la fonction doit ajouter un élément au tas de manière à ce qu'il reste un arbre binaire presque complet
    tout en respectant l'invariant : les valeurs des parents doivent être inférieures à celles des enfants.
    la fonction ne retourne rien.
    """
    # VOTRE CODE

Correction (cliquer pour afficher)

def insert(tas,x):
    tas.append(x)
    n = len(tas)
    enfant = n
    parent = enfant//2
    while enfant > 1 and tas[enfant-1] < tas[parent-1]:
        tas[enfant-1],tas[parent-1] = tas[parent-1],tas[enfant-1]
        enfant = parent
        parent = enfant//2

Test :

Tas = [3,7,8,8,7,12,9,9,8,8,8,13]
insert(Tas,1)
print(Tas)

[1, 7, 3, 8, 7, 8, 9, 9, 8, 8, 8, 13, 12]

def extractMin(tas):
    """
    extractMin(tas: list) -> Min: int 
    la fonction doit retirer la racine du tas 
    tout en respectant l'invariant : les valeurs des parents doivent être inférieures à celles des enfants.
    """
    # VOTRE CODE

Correction (cliquer pour afficher)

def extractMin(tas):
    n = len(tas)
    # on place la racine à la fin et on l'extrait
    tas[n-1],tas[0] = tas[0],tas[n-1]
    Min = tas.pop()
    n -= 1
    # Si le tas ne contient plus qu'1 ou 0 élément, c'est fini
    if n == 0 or n == 1:
        return Min
    # on identifie ensuite le plus petit des deux enfants de la nouvelle racine (ou l'unique enfant s'il n'y en a qu'un...)
    parent = 1
    enfant = plusPetitEnfant(tas,parent)
    # tant que le plus petit enfant est plus petit que son parent, on les permute
    while tas[enfant-1] < tas[parent-1]:
        tas[enfant-1],tas[parent-1] = tas[parent-1],tas[enfant-1]
        # nouveaux parents et enfants
        parent = enfant
        if not plusPetitEnfant(tas,parent):
            break # si le nouveau parent n'a pas d'enfant
        else:
            enfant = plusPetitEnfant(tas,parent)
    return Min

Test :

Tas = [3,7,8,8,7,9,12,9,8,8,8,10]
m = extractMin(Tas)
print(m,Tas)

3 [7, 7, 8, 8, 8, 9, 12, 7, 8, 10, 8]

Construisons maintenant un tri par tas et montrons qu’il est bien plus rapide que le tri par sélection dont il est issu.

def triParSelection(liste):
    n = len(liste)
    for i in range(n-1):
        min = i
        for j in range(i+1,n):
            if liste[j]<liste[min]:
                min = j
        if min != i:
            liste[i], liste[min] = liste[min], liste[i]
    return L

def triParTas(liste):
    T = []
    Ltrie = []
    n = len(liste)
    for e in liste:
        insert(T,e) # on construit un tas à partir de la liste
    for i in range(n):
        Ltrie.append(extractMin(T)) # la recherche du min est remplacé par extractMin
    return Ltrie

L = [-13,12,5,1,95,4]
print(triParSelection(L))
print(triParTas(L))

[-13, 1, 4, 5, 12, 95]
[-13, 1, 4, 5, 12, 95]

from time import time
from random import randint
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = (15, 5)

I, T_trisel, T_tritas = [], [], []
for i in range(100,1000,1):
    L = []
    L = [randint(0,i) for k in range(i)]
    start1 = time()
    triParSelection(L)
    stop1 = time()
    T_trisel.append(stop1-start1)
    start2 = time()
    triParTas(L)
    stop2 = time()
    T_tritas.append(stop2-start2)
    I.append(i)

plt.plot(I,T_trisel,label="tri par sélection")
plt.plot(I,T_tritas,label="tri par tas")

plt.xlabel('taille de la liste')
plt.ylabel("temps d'exécution (s)")
plt.legend()

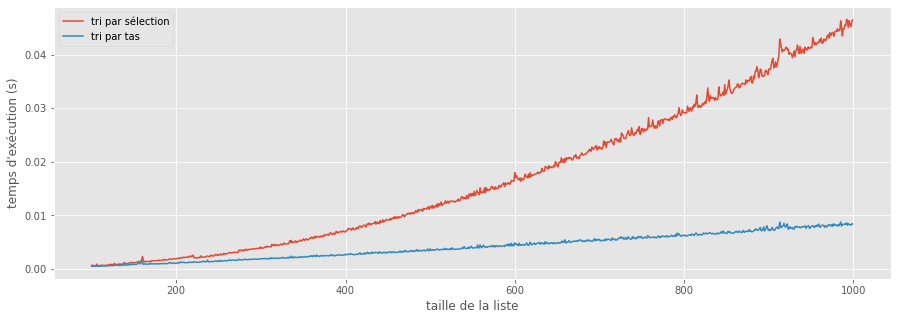
Commentaire (cliquer pour afficher)

Le tri par tas rejoint donc le tri fusion et le tri rapide dans la catégorie des tris comparatifs quasilinéaires (meilleur complexité possible pour un tri à base de comparaisons).

Les graphes nous ont donc ici permis de mettre au point une structure de données capable d’upgrader tout algorithme nécessitant une détermination répétée d’un plus petit (ou grand) élément dans un ensemble.

Parcours d’un graphe

Détecteur de cycle

Les graphes orientés sont générallement utilisés pour représenter un ensemble de dépendances (l’ensemble des prérequis d’un cours, l’ensemble des installations nécessaires au fonctionnement d’un programme, etc…).

Et la présence de cycles dans de tels graphes est synonyme de bloquage (exemple : pour faire la première tâche, vous attendez la seconde, et pour faire la seconde, vous attendez la première…).

Quelle que soit l’application, détecter les cycles est donc primordial pour éviter de se retrouver dans ce type de situation.

Une idée pour détecter un cycle est d’utiliser à nouveau le parcours en profondeur : si on tombe sur un sommet déjà exploré au cours de la progression dans une branche, alors on a affaire à un cycle.

Point important : on suppose ici que les graphes donnés en argument à la fonction sont non orientés.

Le problème que pose ce type de graphe pour la recherche de cycle est la présence systématique du sommet considéré dans la liste de ses voisins (si ‘A’ est le voisin de ‘B’ alors ‘B’ est le voisin de ‘A’) puisqu’un graphe non-orienté permet les aller-retour.

On oriente alors dans un premier temps le graphe non orienté donné en argument en retirant systématiquement de la liste des voisins d’un sommet les sommets dont lui-même est le voisin. On ne sera ainsi plus piégé par un aller-retour entre deux voisins. On peut s’assurer ensuite de la présence d’un cycle si le parcours en profondeur rencontre un sommet présent dans Vus.

Ajoutez donc à la fonction un bout de code qui construit un graphe Go orienté à partir de G.

from collections import deque

def detecteCycles(G,depart):
    """
    detecteCycles(G: dict, depart) -> bool
    depart est une des clés de G
    detecteCycles doit retourner True si un cycle est rencontré
    """
    pile = deque()
    pile.append(depart)
    Vus = {s : False for s in G}
    # on transforme G en un graphe orienté Go
    Go = copy.deepcopy(G) # on veut éviter de modifier G qui est mutable
    # VOTRE CODE
    while pile:
        sommet = pile.pop()
        if not Vus[sommet]:
            Voisins = Go[sommet].copy()
            pile += Voisins
            Vus[sommet] = True
        else: 
            return True
    return False

Correction (cliquer pour afficher)

On ajoute ces 3 lignes avant le while :

for s1 in Go:
    for s2 in Go[s1]:
        Go[s2].remove(s1) # sans deepcopy, on modifierait G

Testez votre fonction sur les trois graphes suivants :

G1 = {'A' : ['B'],
      'B' : ['A','C'],
      'C' : ['B','D','E'],
      'D' : ['C','E'],
      'E' : ['C','D']}
G2 = {'A' : ['B','E'],
      'B' : ['A','C'],
      'C' : ['B','D'],
      'D' : ['C','E'],
      'E' : ['A','D']}
G3 = {'A' : ['B','E'],
      'B' : ['A','C'],
      'C' : ['B','D'],
      'D' : ['C'],
      'E' : ['A']}

Correction (cliquer pour afficher)

print(detecteCycles(G1,'A'))
detecteCycles(G2,'A')
detecteCycles(G3,'A')

True
True
False

Plus court chemin

Une autre application ultra importante des graphes : trouver le plus vite possible le plus court chemin entre deux points.

On peut presque toujours modéliser un déplacement comme un chemin sur un graphe (ou plutôt une chaîne dans le cas présent car nos graphes ne seront pas orientés).

Représentons par exemple la carte d’un petit jeu vidéo sous forme de graphe.
Pour cela, on transforme chaque lieu possible en un sommet et chaque transition possible d’un point à un autre comme une arête.

Créons une petite carte de 20 cases sur 20 avec des déplacements possibles horizontaux, verticaux mais aussi diagonaux d’une case à une case voisine.
Tous les arcs reçoivent d’abord le même poids de 1.

carte = {}
imax = 20
jmax = 20
for i in range(imax):
    for j in range(jmax):
        poids_voisins = {}
        if i > 0:
            poids_voisins[(i-1,j)] = 1
        if j > 0:
            poids_voisins[(i,j-1)] = 1
        if i > 0 and j > 0:
            poids_voisins[(i-1,j-1)] = 1
        if i > 0 and j < jmax-1:
            poids_voisins[(i-1,j+1)] = 1
        if i < imax-1:
            poids_voisins[(i+1,j)] = 1
        if j < jmax-1:
            poids_voisins[(i,j+1)] = 1
        if i < imax-1 and j > 0:
            poids_voisins[(i+1,j-1)] = 1
        if i < imax-1 and j < jmax-1:
            poids_voisins[(i+1,j+1)] = 1
        carte[(i,j)] = poids_voisins

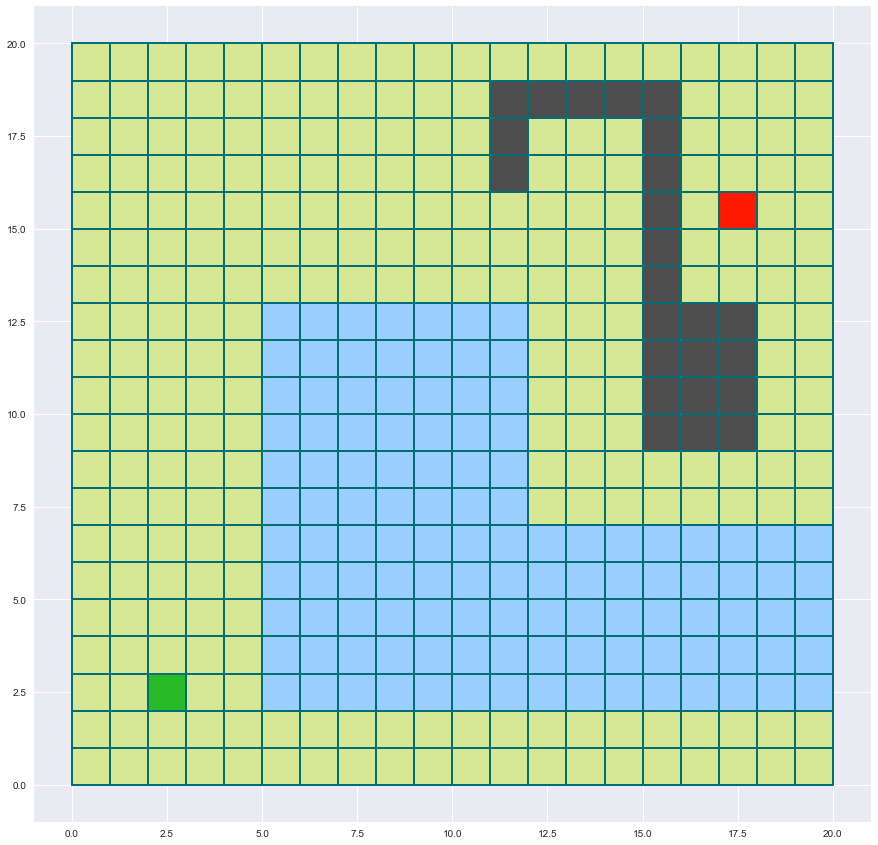
Compliquons notre carte en y rajoutant différents environnements : des marécages où il est difficile de se mouvoir et des murs infranchissables.
Pour modéliser les marécages on va modifier les pondérations : on augmente le poids des arêtes amenant à des sommets s’y trouvant. Et pour les murs, on va retirer du graphe les sommets correspondant.

dessin = {s : 1 for s in carte.keys()} # dictionnaire aidant pour le tracé

# marécages composés de deux rectangles en L
limites_marecages_1 = ((5,11),(2,12)) # le 1er rectangle s'étend de 5 à 19 en largeur, et de 5 à 12 en hauteur
for sommet in carte.keys():
    for voisin in carte[sommet].keys():
        i,j = voisin
        if limites_marecages_1[0][0]<=i<=limites_marecages_1[0][1] and limites_marecages_1[1][0]<=j<=limites_marecages_1[1][1]:
            carte[sommet][voisin] = 5
limites_marecages_2 = ((12,20),(2,6)) # 2eme rectangle
for sommet in carte.keys():
    for voisin in carte[sommet].keys():
        i,j = voisin
        if limites_marecages_2[0][0]<=i<=limites_marecages_2[0][1] and limites_marecages_2[1][0]<=j<=limites_marecages_2[1][1]:
            carte[sommet][voisin] = 5
# pour reconnaître les sommets dans le marécage lors du dessin
for i in range(limites_marecages_1[0][0],limites_marecages_1[0][1]+1):
    for j in range(limites_marecages_1[1][0],limites_marecages_1[1][1]+1):
        dessin[(i,j)] = 5
for i in range(limites_marecages_2[0][0],limites_marecages_2[0][1]+1):
    for j in range(limites_marecages_2[1][0],limites_marecages_2[1][1]+1):
        dessin[(i,j)] = 5

# murs (on retire les sommets concernés (y compris des voisins))
limites_murs = ((11,16),(17,11),(16,11),(15,11),(17,12),(16,12),(15,12),(15,13),(15,14),(15,15),(15,16),(15,17),(15,18),(14,18),(13,18),(12,18),(11,18),(11,17),(15,10),(16,10),(17,10),(15,9),(16,9),(17,9))
# chaque couple (a,b) correspond aux coordonnées d'une case de mur
for sommet in carte.copy().keys():
    for voisin in carte[sommet].copy().keys():
        i,j = voisin
        if (i,j) in limites_murs:
            del carte[sommet][voisin]
for sommet in carte.copy().keys():
    i,j = sommet
    if (i,j) in limites_murs:
        del carte[sommet]

Définissons les sommets de départ et d’arrivée.

depart = (2,2)
arrivee = (17,15)

Et construsions enfin une fonction permettant de tracer la carte en faisant apparaître les marécages, les murs et les points de départ et d’arrivée.

import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
plt.style.use('seaborn')
fig, ax = plt.subplots(figsize=(15,15))

def trace_terrain(dim,dep,arr):
    coul_bords = (0/255,110/255,118/255)
    coul_marec = (155/255,207/255,255/255)
    coul_prairie = (214/255,232/255,147/255)
    coul_murs = (0.3,0.3,0.3)
    coul_depart = (39/255,187/255,40/255)
    coul_arrivee = (255/255,25/255,0/255)
    for i in range(dim[0]):
        for j in range(dim[1]):
            if (i,j) not in carte:
                ax.add_patch(Rectangle((i,j), 1, 1,
                                       edgecolor = coul_bords,
                                       facecolor = coul_murs,
                                       fill=True,
                                       lw=2))
            elif dessin[(i,j)] == 1:
                ax.add_patch(Rectangle((i, j), 1, 1,
                                       edgecolor = coul_bords,
                                       facecolor = coul_prairie,
                                       fill=True,
                                       lw=2))
            else:
                ax.add_patch(Rectangle((i, j), 1, 1,
                                       edgecolor = coul_bords,
                                       facecolor = coul_marec,
                                       fill=True,
                                       lw=2))
    ax.add_patch(Rectangle(dep, 1, 1,
                 edgecolor = coul_bords,
                 facecolor = coul_depart,
                 fill=True,
                 lw=2))
    ax.add_patch(Rectangle(arr, 1, 1,
                 edgecolor = coul_bords,
                 facecolor = coul_arrivee,
                 fill=True,
                 lw=2))
    ax.autoscale_view()

trace_terrain((20,20),depart,arrivee)

Recherche en largeur

Utilisons l’algorithme de recherche en largeur (Breadth-First Search ou BFS) vu en cours pour tenter de trouver la plus petite chaîne de sommets reliant le départ à l’arrivée.

def recherche_largeur(G,depart,arrivee):
    file = [(depart,[depart])]    
    Vus = {}
    while file:
        sommet,chemin = file.pop(0)
        if sommet == arrivee:
            return chemin,Vus
        if not sommet in Vus:
            for s in G[sommet]:
                nv_chemin = chemin+[s]
                file.append((s,nv_chemin))
            Vus[sommet] = True
    return False

Chaîne obtenue :

recherche_largeur(carte,depart,arrivee)[0]

[(2, 2), (3, 2), (4, 2), (5, 2), (6, 2), (7, 2), (8, 2), (9, 2), (10, 2), (11, 2), (12, 3), (13, 4), (14, 5), (15, 6), (16, 7), (17, 8), (18, 9), (18, 10), (18, 11), (18, 12), (17, 13), (16, 14), (17, 15)]

Traçons la chaîne en rose sur la carte :

trace_terrain((20,20),depart,arrivee)
for sommet in recherche_largeur(carte,depart,arrivee)[0][1:-1]:
    ax.add_patch(Rectangle(sommet,1, 1,edgecolor=(0/255,110/255,118/255),facecolor=(255/255,209/255,247/255),fill=True,lw=2))
fig

On constate donc que la recherche en largeur trouve un chemin très court qui évite bien le mur.

Visualisons aussi (en les blanchissant) l’ensemble des sommets inspectés par l’algorithme pour trouver son chemin.

trace_terrain((20,20),depart,arrivee)
for sommet in recherche_largeur(carte,depart,arrivee)[1]:
    ax.add_patch(Rectangle(sommet,1,1,edgecolor=(0/255,110/255,118/255),facecolor=(1,1,1,0.8),fill=True,lw=2))
fig

Quasiment toute la carte a été inspectée…

Répondez aux trois questions suivantes :

le chemin trouvé est-il le plus court possible indépendemment des pondérations ?

le chemin trouvé est-il le plus court possible si on prend en compte les pondérations ?

l’algorithme est-il efficace en terme de nombre de sommets inspectés ?

Correction (cliquer pour afficher)

oui

non

non

Dijkstra

Passons de la recherche en largeur à l’algorithme de Dijkstra. On utilise l’implémentation du cours avec des tas (file de priorité) fournis par le module heapq.

import heapq

def Dijkstra(G, depart, arrivee):
    Scores = {sommet : float('inf') for sommet in G}
    Preds = {sommet : None for sommet in G}
    Scores[depart] = 0
    Vus = {}
    tas = [(0, depart)]
    while tas:
        score_actuel, sommet_actuel = heapq.heappop(tas)
        if sommet_actuel == arrivee:
            return Preds,Scores,Vus
        if score_actuel == Scores[sommet_actuel]:          
            score_voisin = G[sommet_actuel]
            for voisin in score_voisin.keys():
                if voisin not in Vus:
                    Vus[voisin] = True
                score = score_actuel + score_voisin[voisin]
                if score < Scores[voisin]:
                    Scores[voisin] = score
                    Preds[voisin] = sommet_actuel
                    heapq.heappush(tas, (score, voisin))

Preds = Dijkstra(carte,depart,arrivee)[0]

Définissez une fonction qui reconstitue la plus petite chaîne à partir de la liste des prédécesseurs fournie par Dijkstra.

def reconstruction_chaine(predecesseurs,depart,arrivee):
    """
    reconstruction_chemin(predecesseur: dict , depart: tuple , arrivee: tuple) -> chemin: liste de tuples
    predecesseur est un dictionnaire qui pour chaque clé sous forme de tuple (x,y) (un des sommets) donne son prédécesseur là aussi sous forme de tuple (x',y').
    la liste retournée, chaine, doit contenir la liste des sommets (chaque sommet est un tuple (x,y)) allant du depart à l'arrivee.
    """
    s = arrivee
    chaine = [s]
    # VOTRE CODE
    return chaine

Correction (cliquer pour afficher)

def reconstruction_chaine(predecesseurs,depart,arrivee):
    s = arrivee
    chaine = [arrivee]
    while s != depart :
        s = predecesseurs[s]
        chaine = [s] + chaine
    return chaine

chaine_Dijk = reconstruction_chaine(Preds,depart,arrivee)

Vérifiez que votre chaîne est bien la même que celle ci-dessous :

chaine_Dijk = [(2, 2), (1, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (1, 9), (2, 10), (3, 11), (4, 12), (5, 13), (6, 14), (7, 15), (8, 16), (9, 17), (10, 18), (11, 19), (12, 19), (13, 19), (14, 19), (15, 19), (16, 18), (16, 17), (16, 16), (17, 15)]

Traçons la chaîne obtenue.

trace_terrain((20,20),depart,arrivee)
for sommet in chaine_Dijk[1:-1]:
    ax.add_patch(Rectangle(sommet,1,1,edgecolor=(0/255,110/255,118/255),facecolor=(255/255,209/255,247/255),fill=True,lw=2))
fig

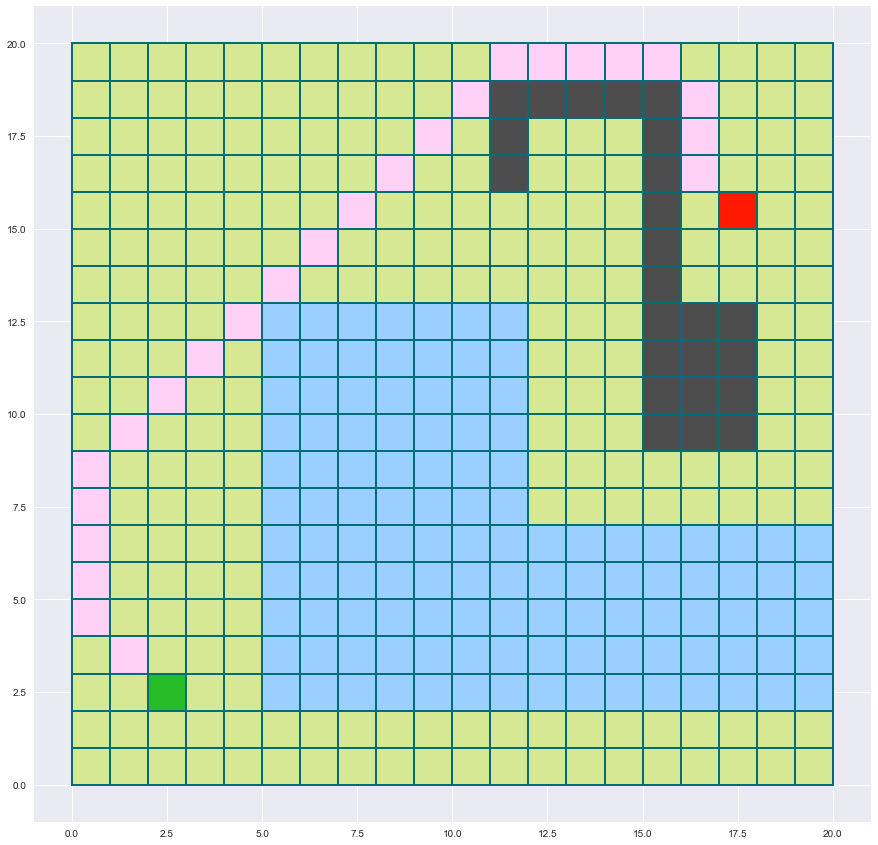
On constate que le chemin trouvé par Dijkstra prend maintenant soin de contourner le marécage.

trace_terrain((20,20),depart,arrivee)
for sommet in Dijkstra(carte,depart,arrivee)[2]:
    ax.add_patch(Rectangle(sommet,1,1,edgecolor=(0/255,110/255,118/255),facecolor=(1,1,1,0.8),fill=True,lw=2))
fig

À nouveau, une grande partie de la carte est inspectée.

Répondez aux trois questions suivantes :

le chemin trouvé est-il le plus court possible indépendemment des pondérations ?

le chemin trouvé est-il le plus court possible si on prend en compte les pondérations ?

l’algorithme est-il efficace en terme de nombre de sommets inspectés ?

Correction (cliquer pour afficher)

non

oui

non

Ajout d’une heuristique

Pour améliorer la vitesse des algorithmes précédents, on va leur ajouter une heuristique. Une heuristique est une petite recette, une règle simple, que l’algorithme va suivre pour s’économiser des étapes.

Le point noir des algorithmes précédents est qu’ils semblent contraints de parcourir quasiment toute la carte avant d’être sûr d’avoir trouvé le bon chemin.
On va les aider en les guidant vers l’arrivée.

L’heuristique va donc consister à guider le choix du prochain sommet de manière à ce qu’il diminue la distance jusqu’à l’arrivée. On le dirrige en quelque sorte vers sa destination…

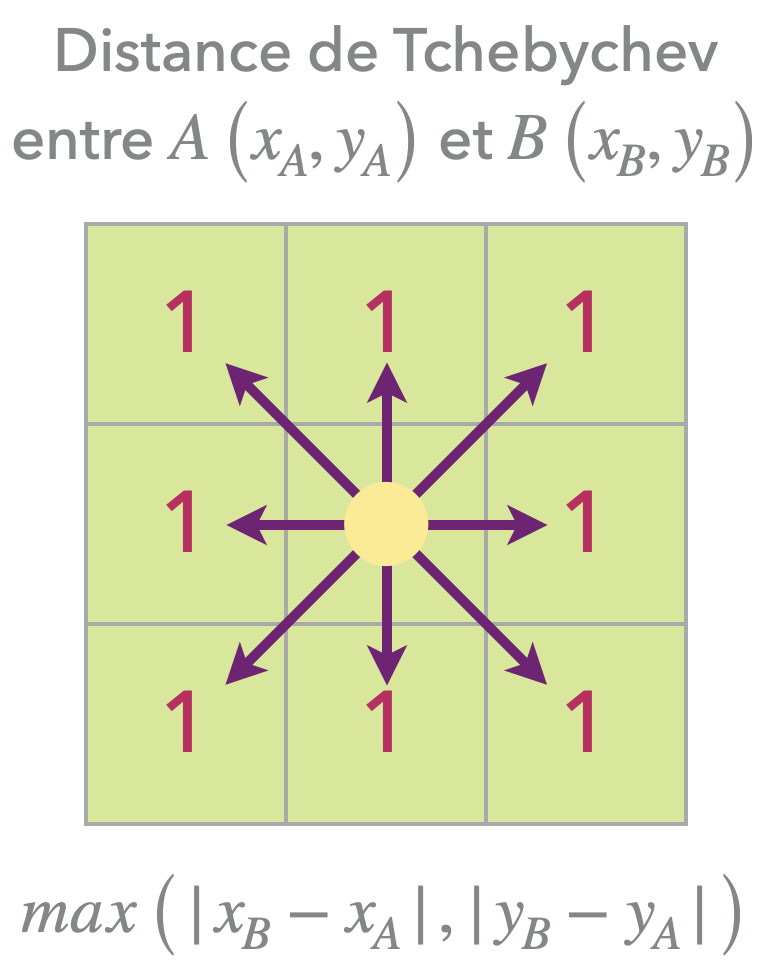
Implémentons donc une fonction distance qui donne la distance entre deux sommets A et B.
Mais quelle distance ? Plusieurs définition non équivalentes sont possibles : distance euclidienne, distance de Manhattan…
Ici, on va utiliser la distance de Tchebychev qui correspond à la distance sur un échiquier où les mouvements en diagonale coûte 1.

def distance(A,B): 
    x_A,y_A = A
    x_B,y_B = B
    X = abs(x_B-x_A)
    Y = abs(y_B-y_A)
    return max(X,Y)

Implémentons maintenant une variante de la recherche en largeur qui intègre l’heuristique grâce à un tas : pour chaque nouveau voisin inspecté, on calcule sa distance à l’arrivée puis on l’ajoute à un tas avec cette distance comme clé de classement.
On s’assure ainsi à chaque itération de retirer du tas le sommet rapprochant le plus de la destination finale.
Il s’agit à nouveau d’un algorithme glouton.

import heapq

def bfs_glouton(G,depart,arrivee):
    tas = [(0, depart)]
    Vus = {}
    Preds = dict()
    Preds[depart] = None
    while tas:
        dist_actuelle, sommet_actuel = heapq.heappop(tas) # on retire le sommet le plus proche de l'arrivée
        if sommet_actuel == arrivee:
            return Preds,Vus
        for voisin in G[sommet_actuel]:
            if voisin not in Vus:
                Vus[voisin] = True
            if voisin not in Preds:
                dist = distance(arrivee, voisin)
                heapq.heappush(tas, (dist, voisin)) # on place dans le tas le voisin affublé de sa distance
                Preds[voisin] = sommet_actuel

chaine_glouton = reconstruction_chaine(bfs_glouton(carte,depart,arrivee)[0],depart,arrivee)

trace_terrain((20,20),depart,arrivee)
for sommet in chaine_glouton[1:-1]:
    ax.add_patch(Rectangle(sommet,1,1,edgecolor=(0/255,110/255,118/255),facecolor=(255/255,209/255,247/255),fill=True,lw=2))
fig

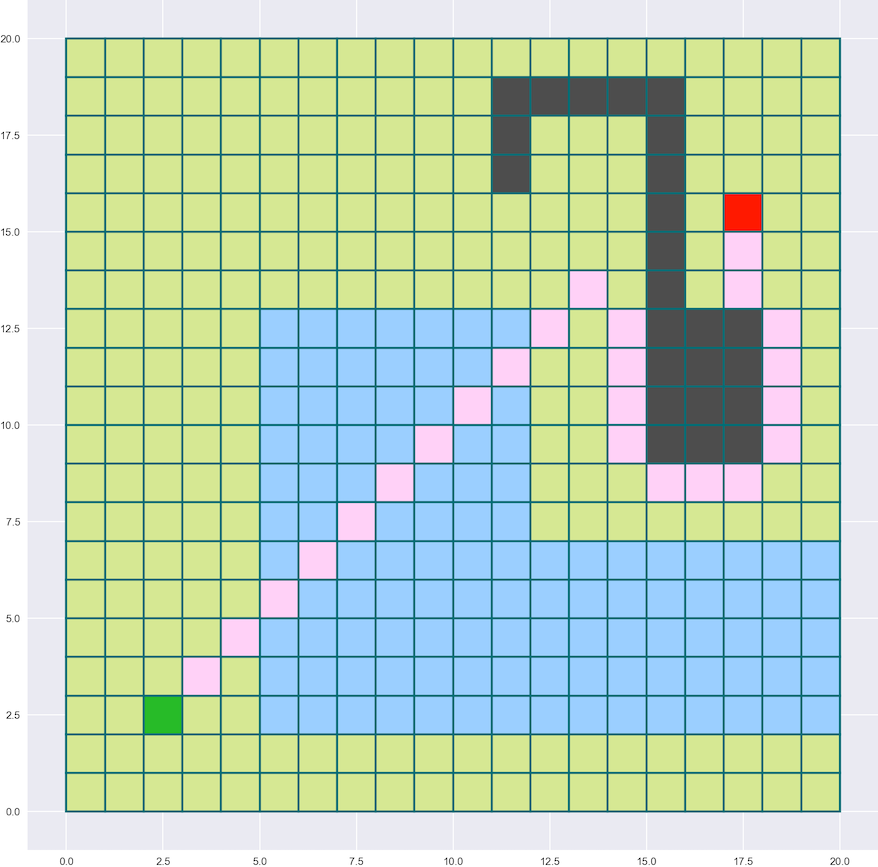
On voit que le chemin se dirige tout de suite vers l’arrivée, jusqu’à rencontrer un mur…

trace_terrain((20,20),depart,arrivee)
for sommet in bfs_glouton(carte,depart,arrivee)[1]:
    ax.add_patch(Rectangle(sommet,1,1,edgecolor=(0/255,110/255,118/255),facecolor=(1,1,1,0.8),fill=True,lw=2))
fig

Le nombre de sommets inspectés a spectaculairement diminué !

Répondez aux trois questions suivantes :

le chemin trouvé est-il le plus court possible indépendemment des pondérations ?

le chemin trouvé est-il le plus court possible si on prend en compte les pondérations ?

l’algorithme est-il efficace en terme de nombre de sommets inspectés ?

Correction (cliquer pour afficher)

non

non

oui

A*

Appliquons maintenant l’heuristique à l’algorithme de Dijkstra. On obtient l’algorithme A* (A étoile ou A star).

def Astar(G, depart, arrivee):
    Scores = {sommet : float('inf') for sommet in G}
    Preds = {sommet : None for sommet in G}
    Scores[depart] = 0
    Vus = {}
    tas = [(0, 0, depart)]
    while tas:
        _, score_actuel, sommet_actuel = heapq.heappop(tas) # on utilise par convention '_' pour déballer un élément d'un tuple dont on ne fera pas usage.
        if sommet_actuel == arrivee:
            return Preds,Scores,Vus
        if score_actuel == Scores[sommet_actuel]:          
            score_voisin = G[sommet_actuel]
            for voisin in score_voisin.keys():
                if voisin not in Vus:
                    Vus[voisin] = True
                score = score_actuel + score_voisin[voisin]
                if score < Scores[voisin]:
                    Scores[voisin] = score
                    Preds[voisin] = sommet_actuel
                    heuristique = score + distance(voisin,arrivee)
                    heapq.heappush(tas, (heuristique, score, voisin))

chaine_Astar = reconstruction_chaine(Astar(carte,depart,arrivee)[0],depart,arrivee)

trace_terrain((20,20),depart,arrivee)
for sommet in chaine_Astar[1:-1]:
    ax.add_patch(Rectangle(sommet,1,1,edgecolor=(0/255,110/255,118/255),facecolor=(255/255,209/255,247/255),fill=True,lw=2))
fig

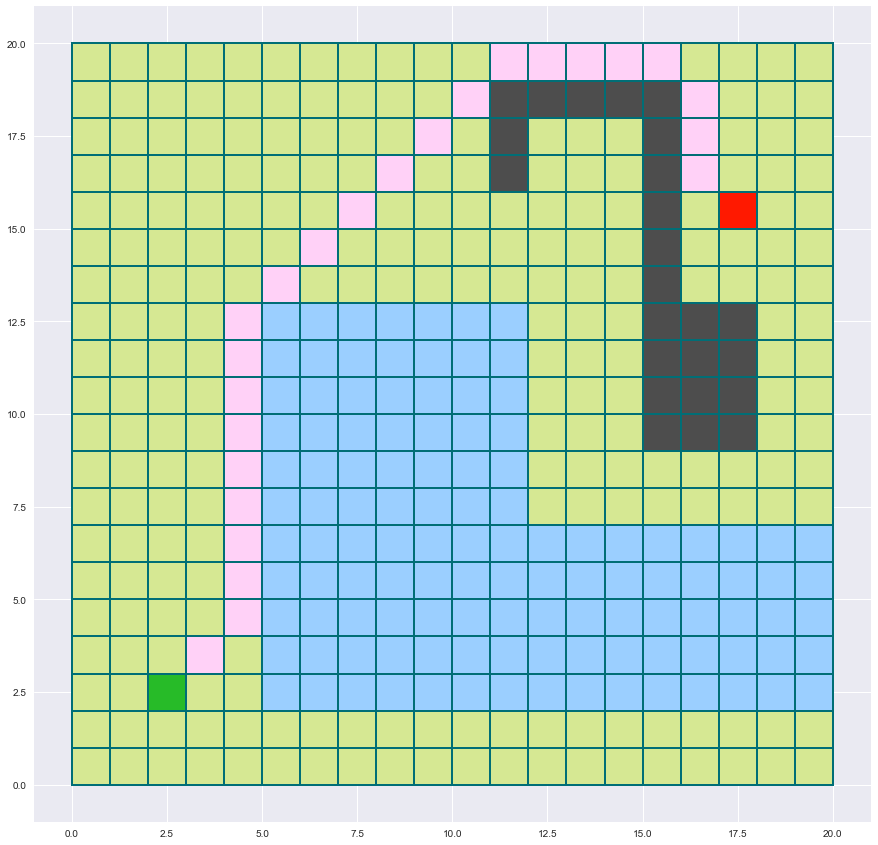
trace_terrain((20,20),depart,arrivee)
for sommet in Astar(carte,depart,arrivee)[2]:
    ax.add_patch(Rectangle(sommet,1,1,edgecolor=(0/255,110/255,118/255),facecolor=(1,1,1,0.8),fill=True,lw=2))
fig

Répondez aux trois questions suivantes :

le chemin trouvé est-il le plus court possible indépendemment des pondérations ?

le chemin trouvé est-il le plus court possible si on prend en compte les pondérations ?

l’algorithme est-il efficace en terme de nombre de sommets inspectés ?

Correction (cliquer pour afficher)

non

oui

oui

Évolutions comparées de recherche_largeur et de Dijkstra :
Évolutions comparées de bfs_glouton et de Astar (vidéo ralentie 2$\times$ par rapport à la précédente) :

	A	B	C	D	E	F	G	H	I	J
A	0	3	2	2	1	6	4	2	6	5
B	3	0	6	6	4	3	6	5	4	5
C	2	6	0	6	2	3	1	1	2	6
D	2	6	6	0	4	3	2	2	4	6
E	1	4	2	4	0	3	6	1	6	2
F	6	3	3	3	3	0	6	2	6	6
G	4	6	1	2	6	6	0	4	2	5
H	2	5	1	2	1	2	4	0	4	2
I	6	4	2	4	6	6	2	4	0	2
J	5	5	6	6	2	6	5	2	2	0

	A	B	C	D	E	F	G	H	I	J
A	0	3	2	2	1	6	4	2	6	5
B	3	0	6	6	4	3	6	5	4	5
C	2	6	0	6	2	3	1	1	2	6
D	2	6	6	0	4	3	2	2	4	6
E	1	4	2	4	0	3	6	1	6	2
F	6	3	3	3	3	0	6	2	6	6
G	4	6	1	2	6	6	0	4	2	5
H	2	5	1	2	1	2	4	0	4	2
I	6	4	2	4	6	6	2	4	0	2
J	5	5	6	6	2	6	5	2	2	0

	A	B	C	D	E	F	G	H	I	J
A	0	3	2	2	1	6	4	2	6	5
B	3	0	6	6	4	3	6	5	4	5
C	2	6	0	6	2	3	1	1	2	6
D	2	6	6	0	4	3	2	2	4	6
E	1	4	2	4	0	3	6	1	6	2
F	6	3	3	3	3	0	6	2	6	6
G	4	6	1	2	6	6	0	4	2	5
H	2	5	1	2	1	2	4	0	4	2
I	6	4	2	4	6	6	2	4	0	2
J	5	5	6	6	2	6	5	2	2	0