Algorithmes pour l’Intelligence Artificielle
L’intelligence arificielle (IA) est une discipline scientifique qui a vu officiellement le jour en 1956. Elle repose sur la conjecture selon laquelle toutes les fonctions cognitives, en particulier l’apprentissage, le raisonnement, le calcul, la perception, la mémorisation, voire la découverte scientifique ou la créativité artistique, peuvent être décrites avec une précision telle qu’il serait possible de les reproduire sur des ordinateurs.
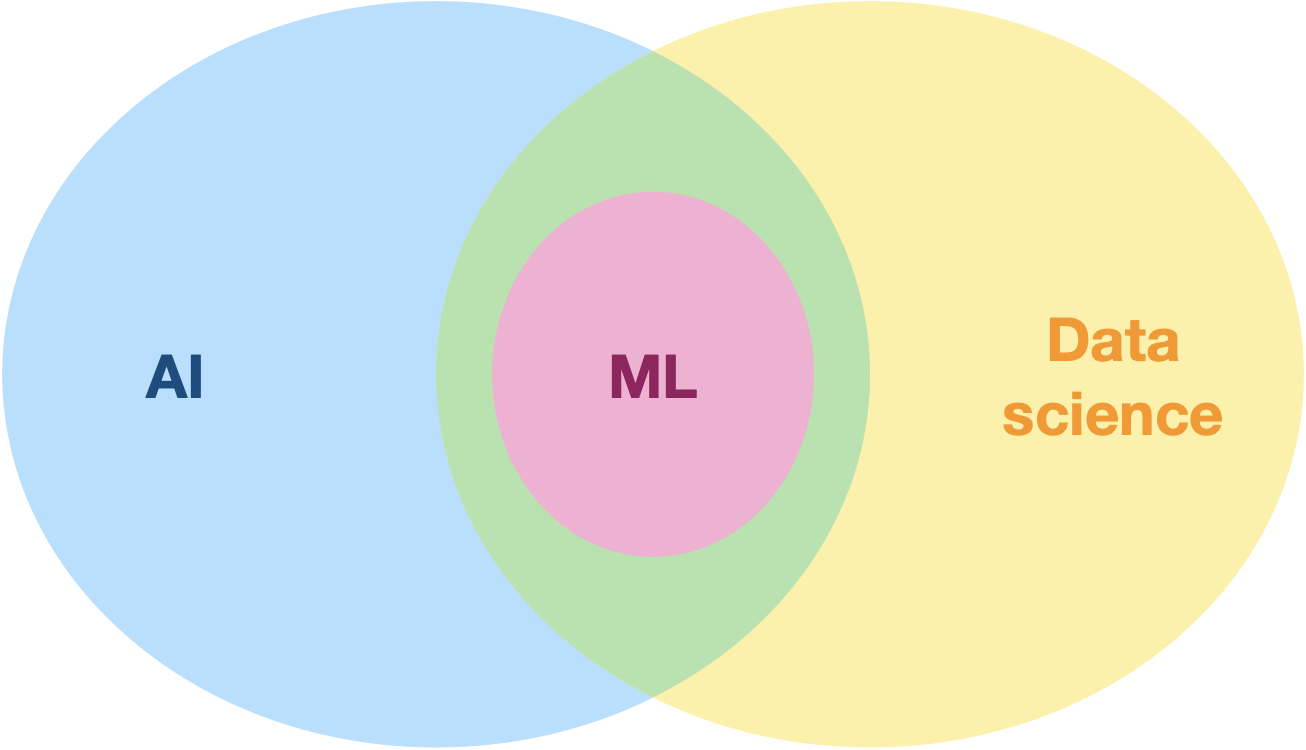
L’apprentissage automatique (Machine Learning) est à l’intersection de l’IA et d’un autre champ scientifique : la science des données (data science).
Arthur Samuel définit l’apprentissage automatique ainsi en 1959 :
La capacité à apprendre sans avoir été spécifiquement programmé pour.
En pratique, il s’agit de produire des réponses adaptées aux données fournies en entrée (identifier des motifs, des tendances, construire des modèles, faire des prédictions). L’apprentissage automatique n’est donc ni plus ni moins que du traitement de données visant à prédire des résultats en fonction des données entrantes.
L’infographie suivante survole le domaine.
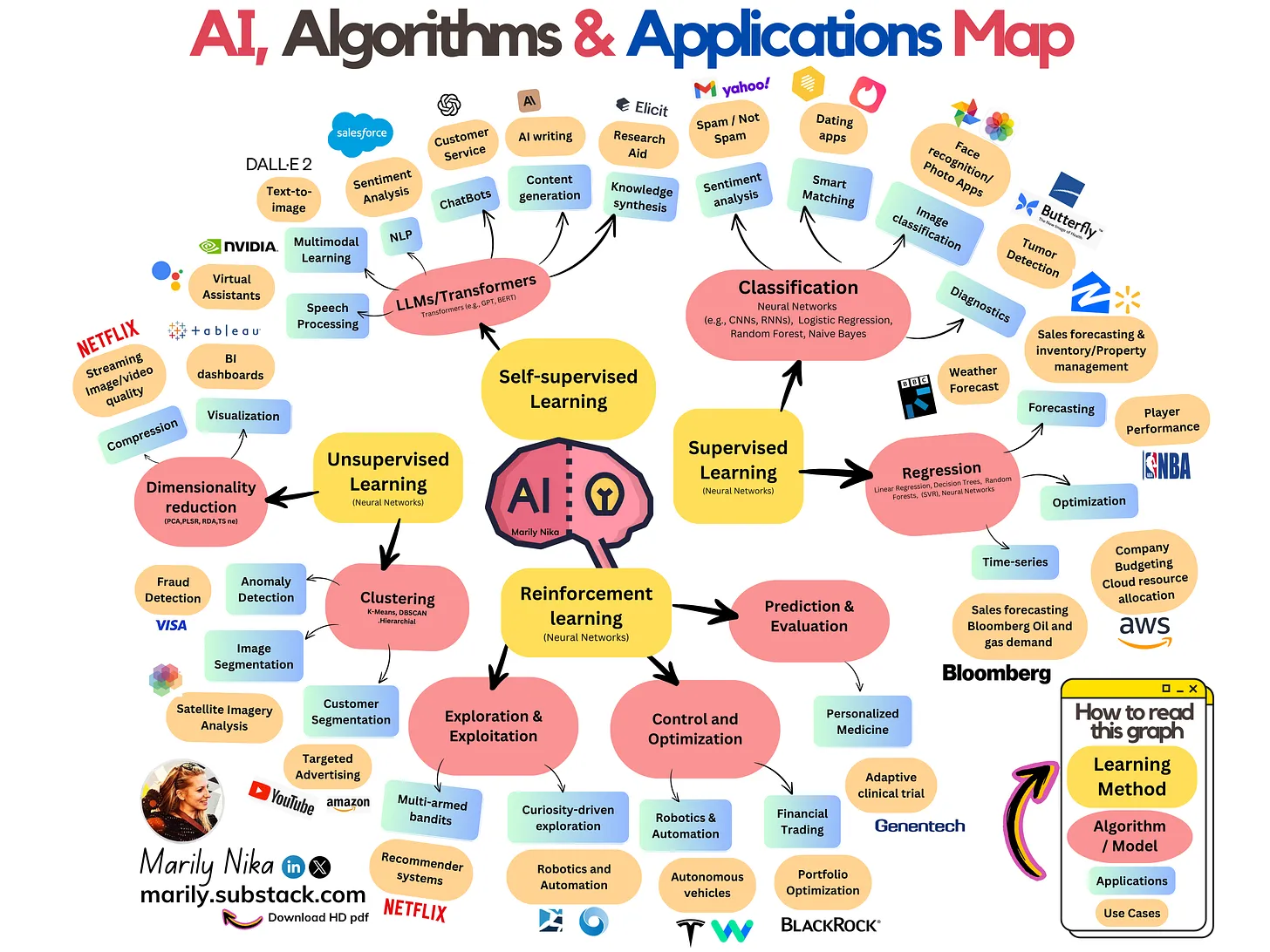
On va s’intéresser dans ce cours à l’apprentissage automatique dit “classique”1 qui regroupe des algorithmes très simples nés dans les années 50 et toujours utilisés aujourd’hui à peu près partout.
Cette branche classique de l’apprentissage automatique se décompose prinicipalement en deux familles d’algorithmes : l’apprentissage supervisé et son pendant, l’apprentissage non supervisé. Nous allons étudier un algorithme star de chacune de ces familles.
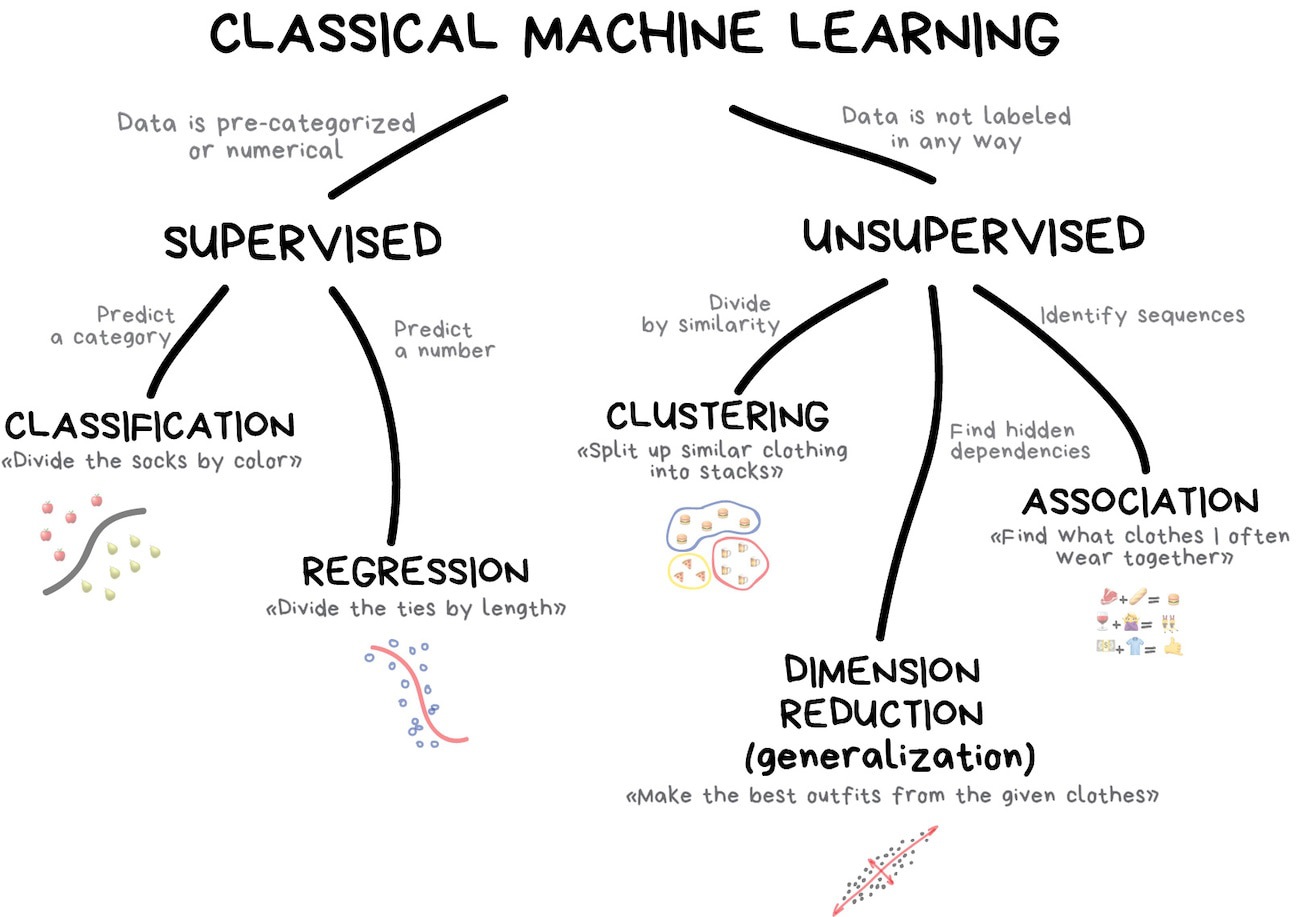
Algorithme des k plus proches voisins – Exemple d’apprentissage supervisé
L’algorithme des k plus proches voisin (k-nearest neighbors ou KNN) est une des techniques les plus simples en apprentissage automatique. Sa facilité d’utilisation et sa rapidité en font un outil de choix dans l’industrie.
KNN est un algorithme d’apprentissage supervisé ; cela signifie que l’algorithme nécessite des données classifiées en amont qui vont lui servir à trouver la bonne étiquette pour d’autres données non encore classifiées.
Suivant la nature de l’étiquette, KNN peut servir à :
- une classification des nouvelles données si les étiquettes sont des catagories ;
- une régression si les étiquettes sont des nombres.
Principe
KNN enregistre, dans un premier temps, tous les points de données étiquetées qui vont lui servir à l’apprentissage (c’est le training set). Puis, quand arrive un point de donnée non étiqueté, l’algorithme calcule sa distance aux autres points et sélectionne les k plus proches. On a alors deux cas possibles :
- si les étiquettes sont des catégories, l’algorithme calcule le mode des catégories des voisins sélectionnés (catégorie la plus représentée).
- si les étiquettes sont des nombres, l’algorithme calcule la moyenne des étiquettes des voisins sélectionnés.
L’algorithme des k plus proches voisins est non paramétrique dans le sens où aucun modèle mathématique de classification ou régression n’est construit à partir des données (pas de paramètre à ajuster) puisque toutes les données d’apprentissage sont enregistrées telles quelles.
Cela signifie qu’on ne présuppose rien de particulier sur les données (à part que des points proches appartiennent à la même catégorie). L’algorithme est donc particulièrement robuste (les données parlent d’elles-même) et simple à mettre à jour (suffit d’ajouter les nouvelles données d’apprentissage).
Choix de k
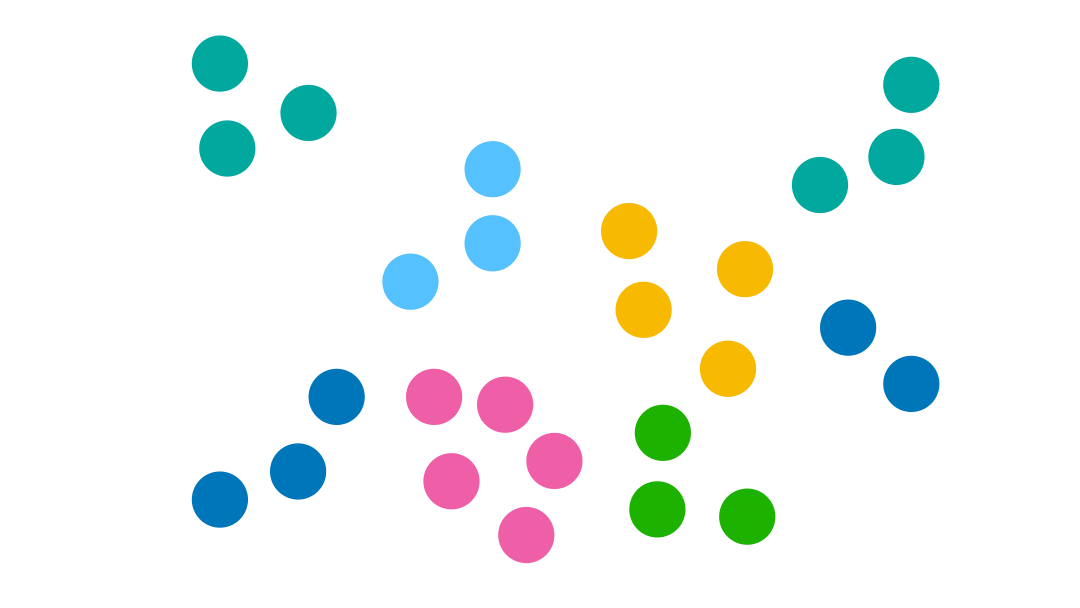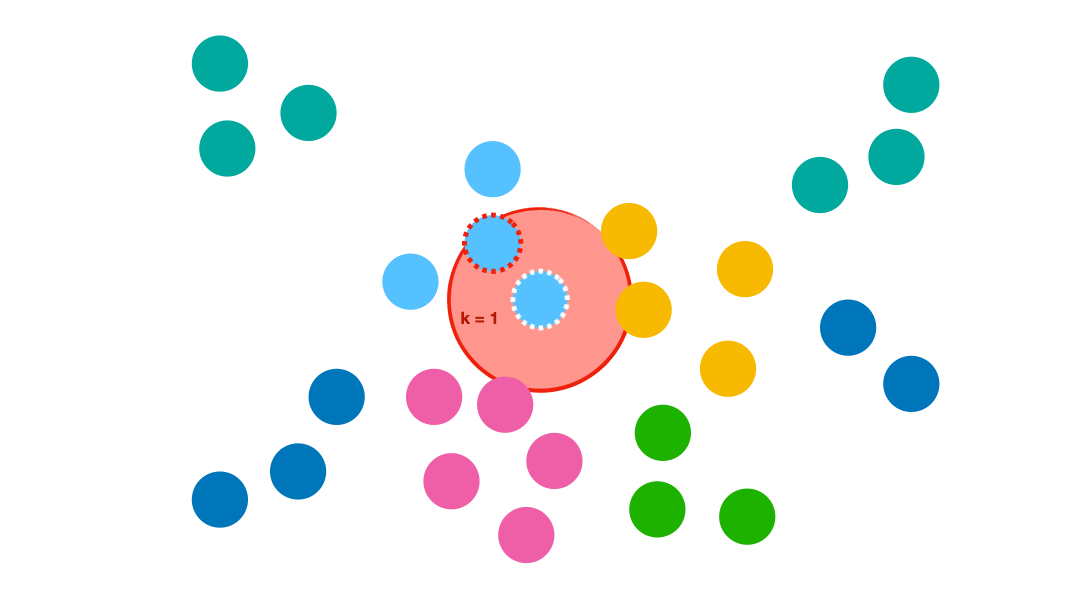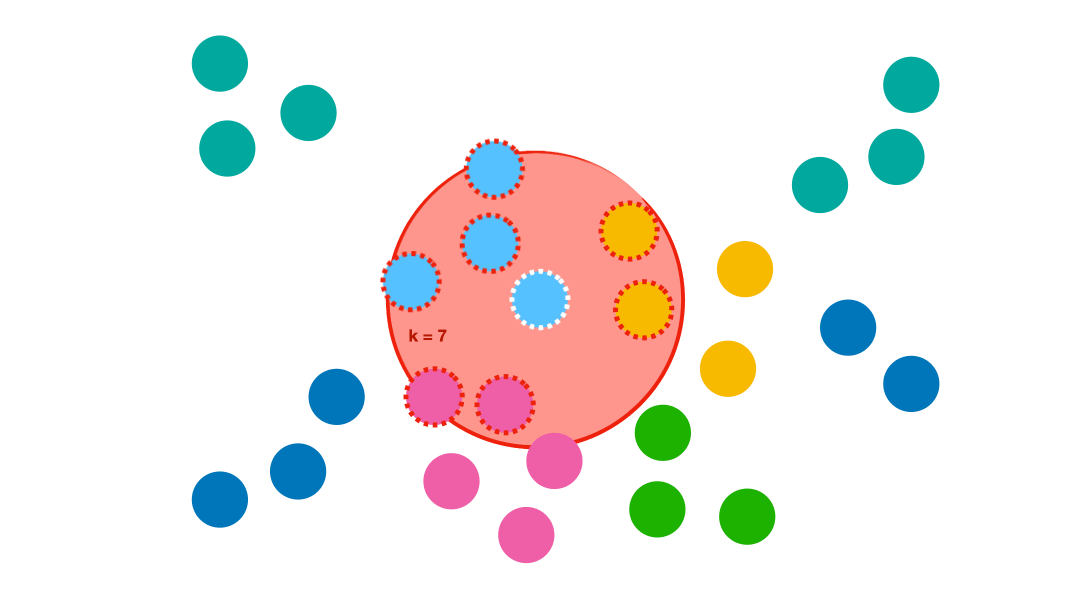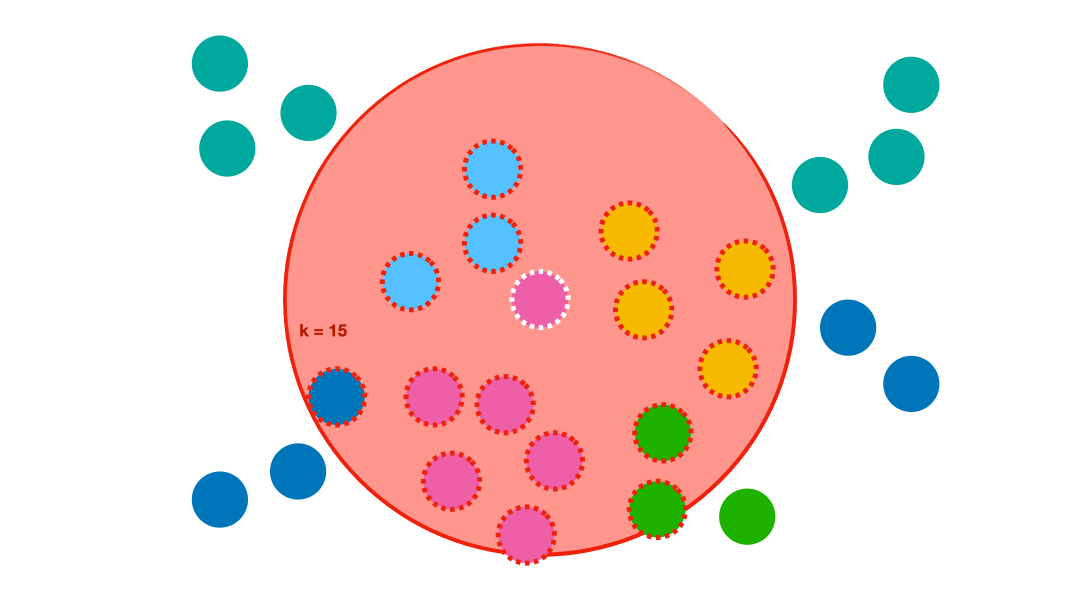
Comme le montre la petite animation ci-dessus, le choix de k modifie le résultat obtenu.
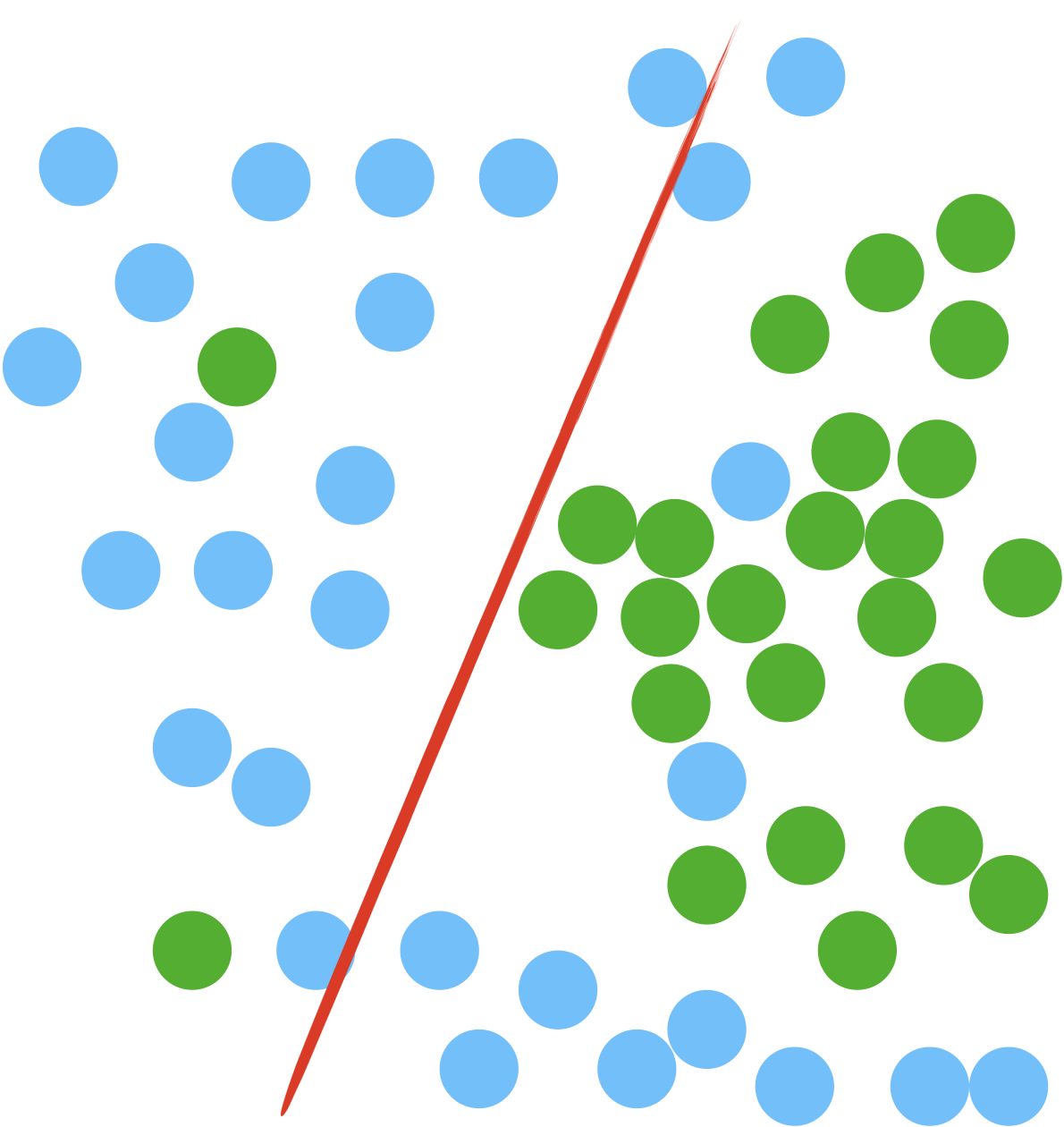
- Si k est trop petit, le moyennage est faible et donc la variabilité va être très grande. On parle alors de surapprentissage (overfitting).
- En augmentant k, les résultats obtenus se stabilisent (vote de la majorité) et les erreurs diminuent, jusqu’au moment où la boule à l’intérieur de laquelle se fait le moyennage devient trop grosse, amenant in fine l’algorithme a choisir systématiquement la catégorie majoritaire, quel que soit le point… On augmente alors le biais (ici, le biais est le préjudice en faveur du plus grand nombre). L’ajustement ne suit plus les variations, on parle de sous-apprentissage (underfitting).
Pour résumer :
| variance | biais | Cas d’une régression | Cas d’une classification | |
|---|---|---|---|---|
| k trop petit $\rightarrow$ overfitting | forte | faible | 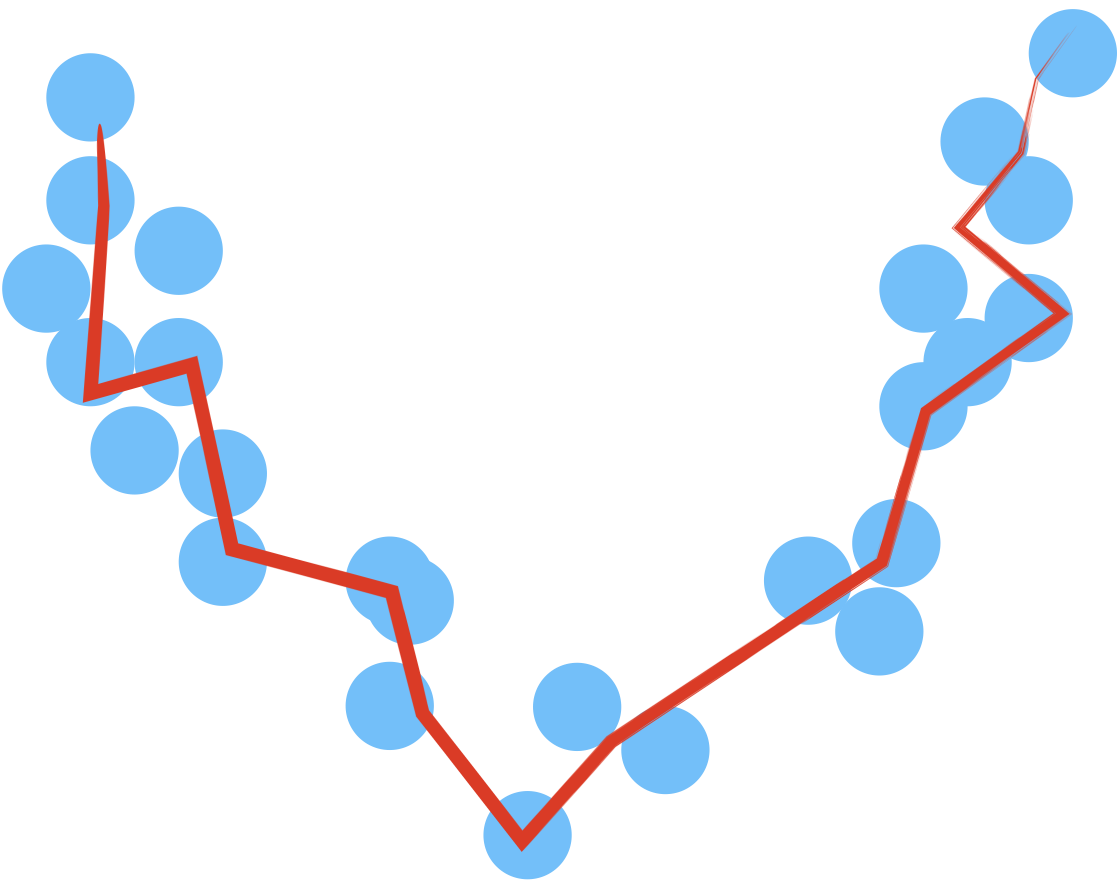 |
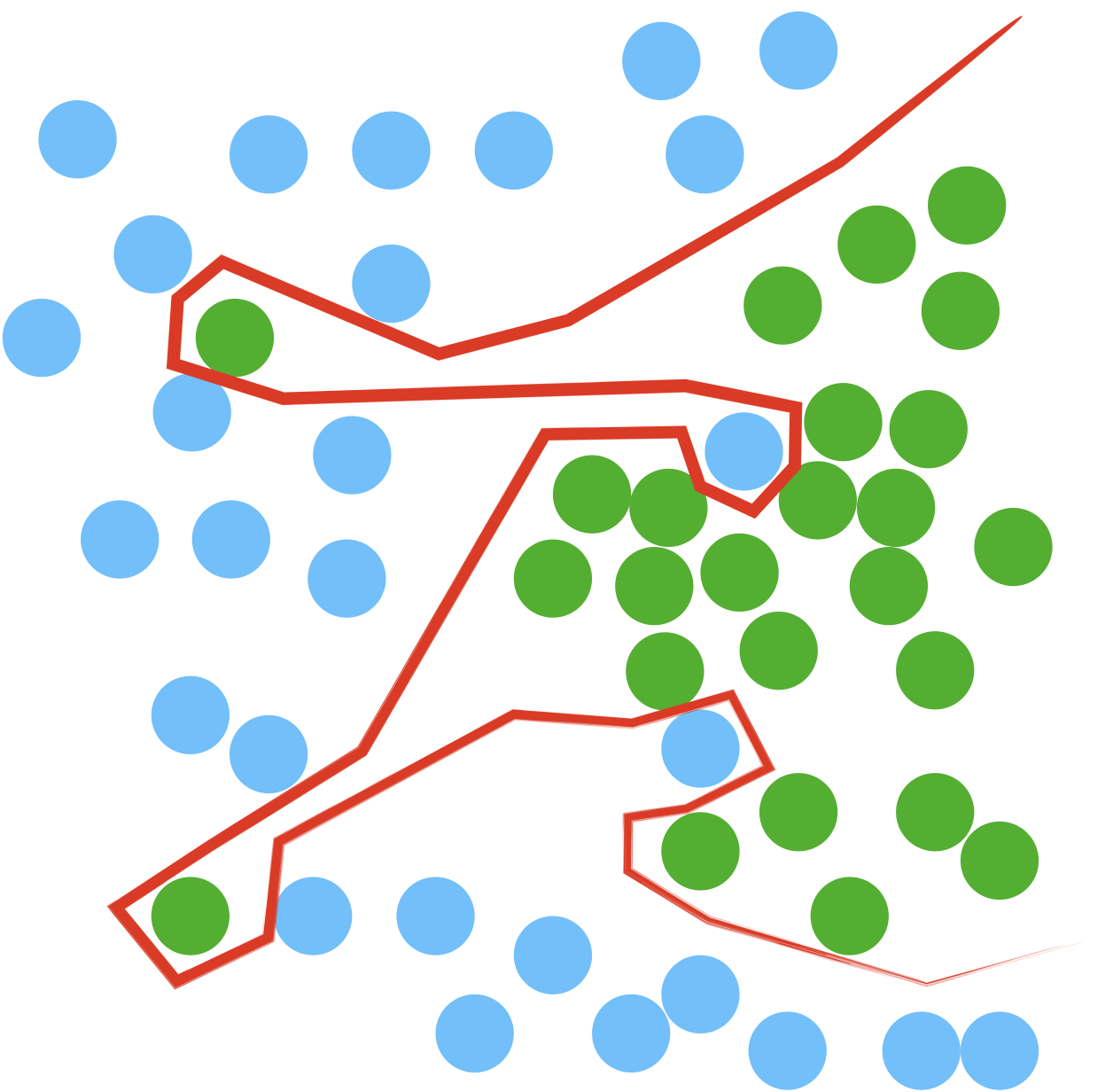 |
| k trop grand $\rightarrow$ underfitting | faible | fort | 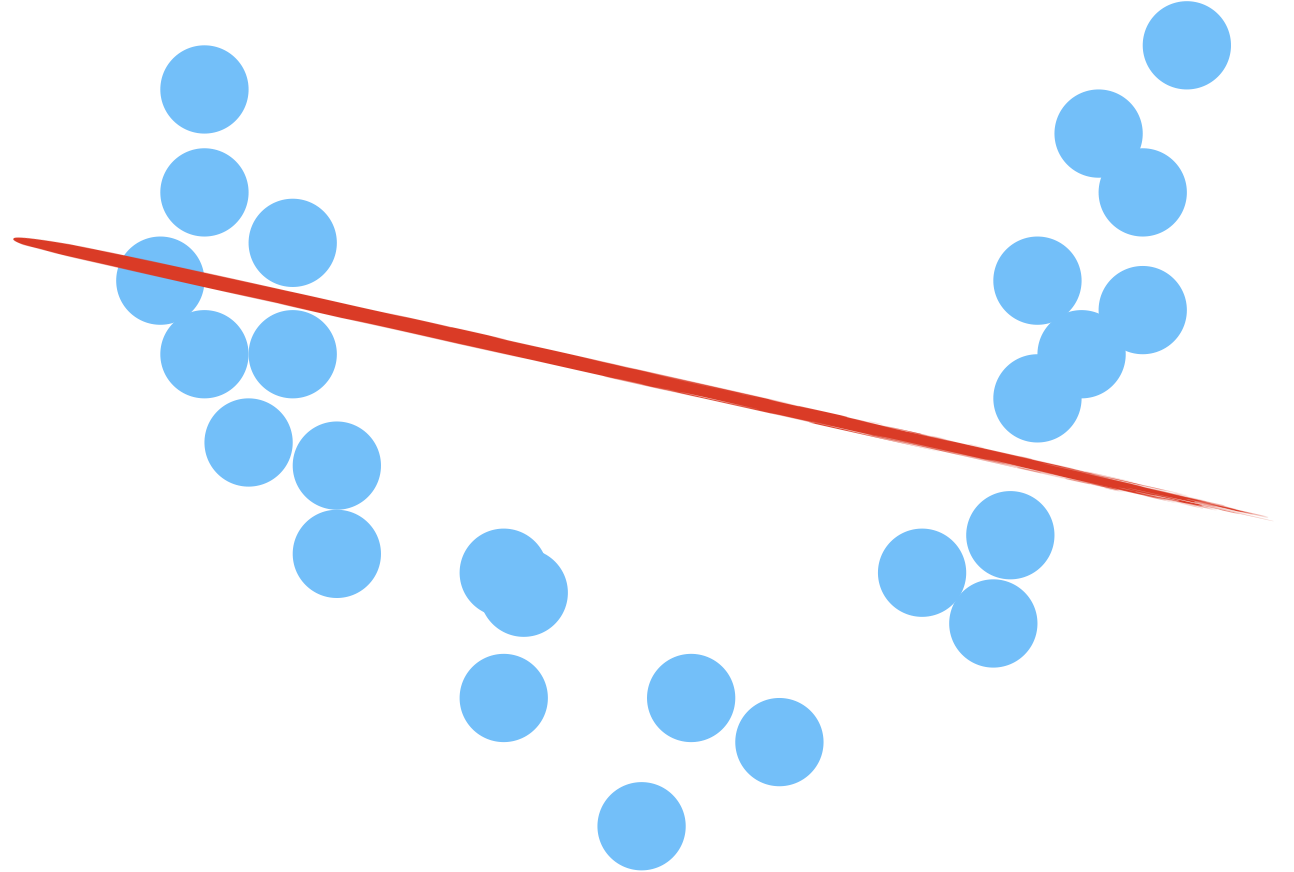 |
 |
Lorsqu’on ne connaît rien sur les données, on peut toujours commencer par prendre la racine carrée du nombre de points dans l’ensemble d’entraînement comme k de départ.
Le choix de k est donc affaire de compromis. Pour le rendre plus scientifique, on peut chercher à mesurer la performance de l’algorithme pour différentes valeurs de k.
Mais comment mesure-t-on la performance d’un algorithme d’apprentissage automatique ?
Validation – Matrice de confusion
La matrice de confusion permet d’évaluer la qualité des prédictions d’un algorithme.
Prenons l’exemple de l’utilisation de KNN sur une banque d’images de chiffres écrits à la main et plus spécifiquement concentrons-nous sur sa capacité à reconnaître des “3”.

On découpe l’espace en 4 cadrans. Sur une dimension, on regroupe d’un côté les données pertinentes (les 3) et de l’autre le reste des données (les non 3), et on décompose l’autre dimension en prédictions positives (les 3 prédits) et négatives (les non 3 prédits).
Puis on compte dans chaque cadran le nombre de données correspondant au recouvrement des prédictions et de la réalité. Un nom issu du vocabulaire des diagnostics médicaux est attribué à chacun de ces cadrans :
- les vrais positifs VP (les 3 identifiés comme des 3),
- les vrais négatifs VN (les non 3 identifiés comme des non 3),
- les faux positifs FP (les non 3 identifiés comme des 3),
- les faux négatifs FN (les 3 identifiés comme des non 3).
À partir de ces effectifs, on peut calculer 3 grandeurs permettant d’évaluer la qualité de la prédiction :
Nombre de données bien prédites parmi les prédictions positives : $$\frac{VP}{VP+FP}$$
Nombre de données bien prédites parmi les données positives :
$$\frac{VP}{VP+FN}$$
$$\frac{VP+VN}{VP+VN+FP+FN}$$
Un algorithme peut très bien être très précis (les prédictions positives sont bien des 3), mais peu sensible, avec un faible taux de rappel (parmi tous les 3, peu ont été identifiés).
À l’inverse, on peut avoir une bonne sensibilité (la plupart des vrais 3 ont été identifiés comme tel), mais peu précis (beaucoup de chiffres identifiés comme des 3 sont en fait d’autres chiffres).
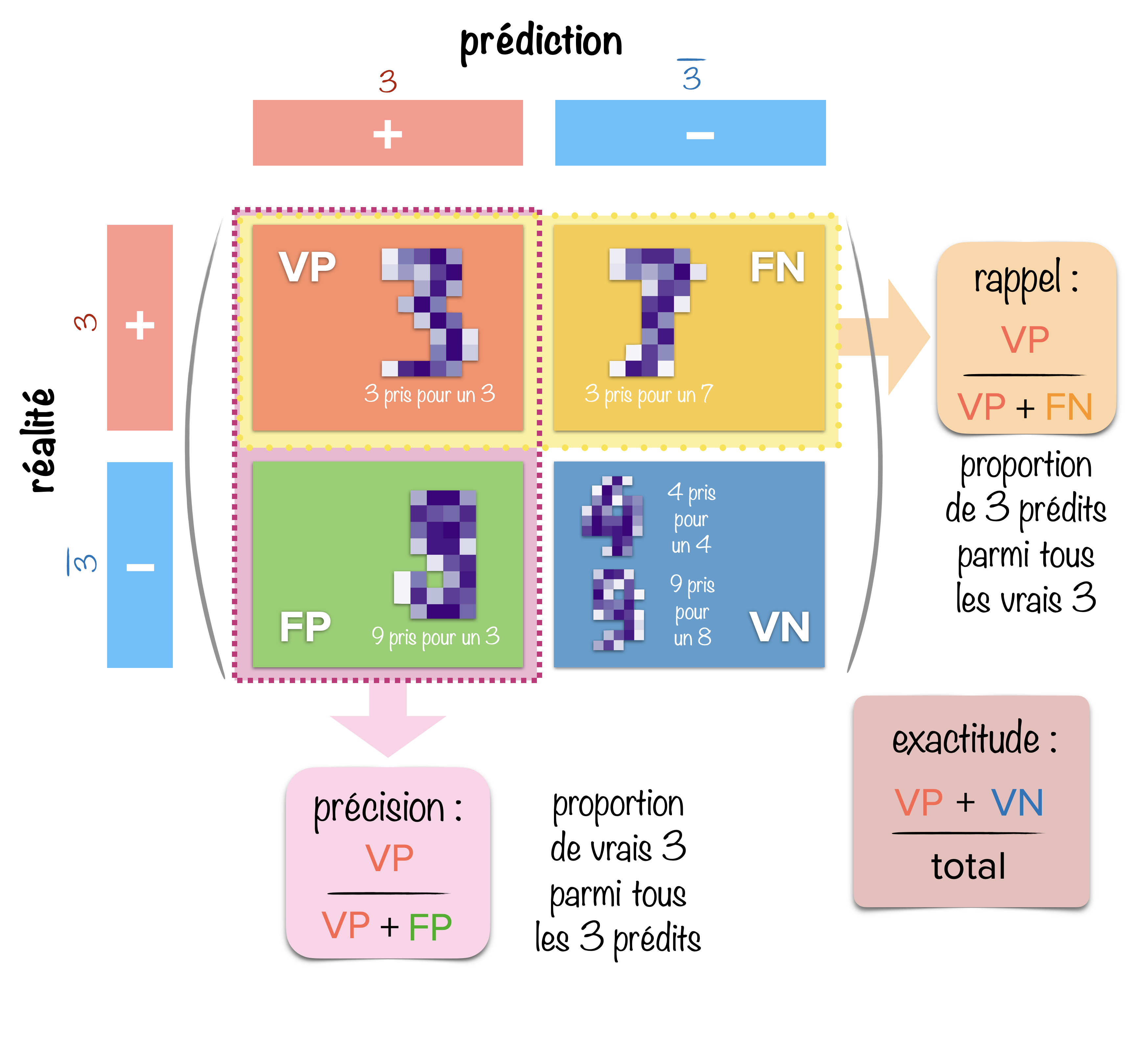
On peut tout aussi bien définir la matrice de confusion avec les prédictions sur les lignes et la réalité sur les colonnes.
Maintenant qu’on sait évaluer l’algorithme, cherchons la valeur de k qui maximise l’exactitude.
Dans le graphe ci-dessous, on a tracé l’exactitude de l’algorithme pour la reconnaissance des “9” en fonction de la valeur de k (ce sont les mêmes jeux de données test et d’apprentissage que dans le TP).
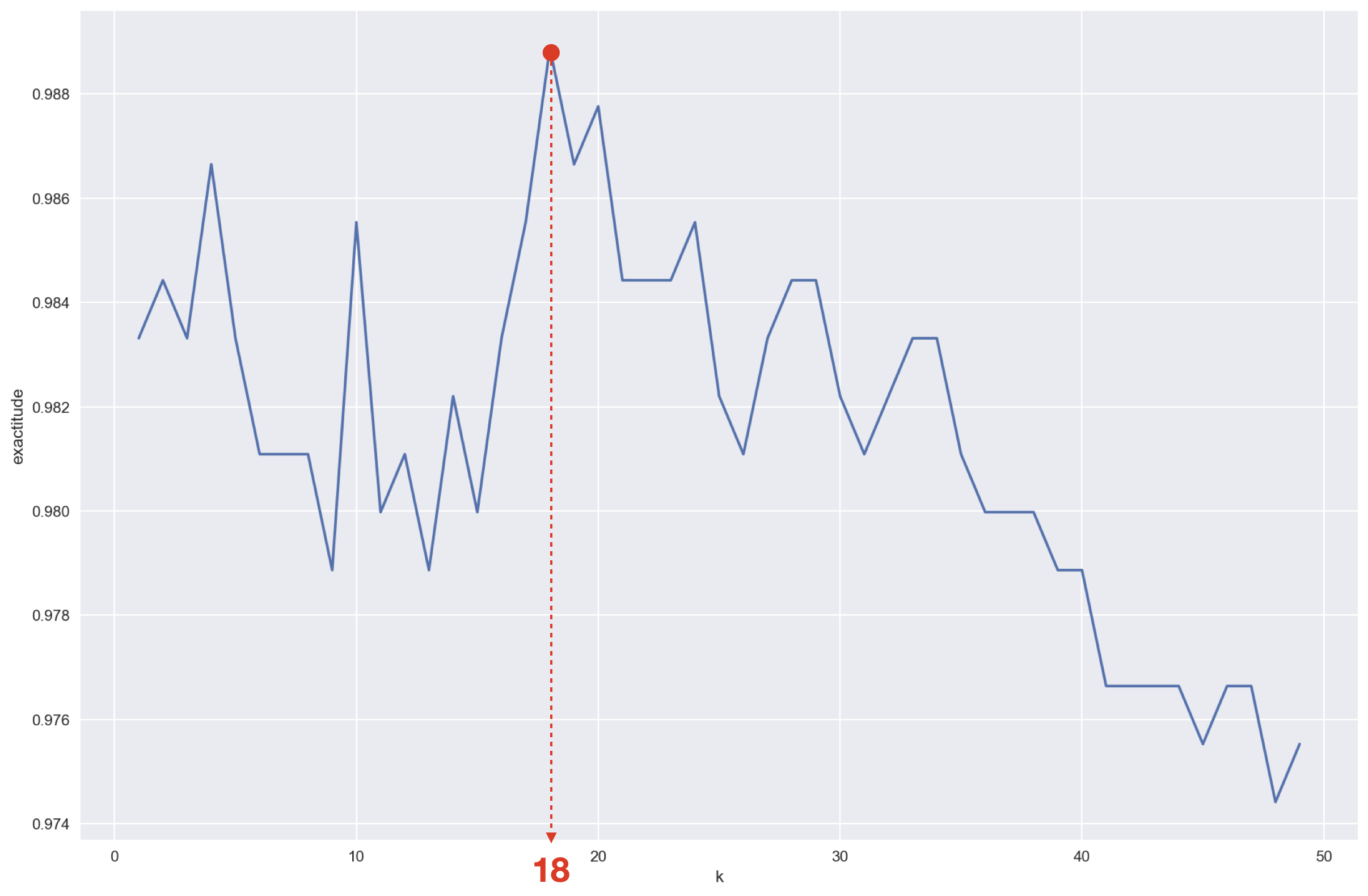 Si notre but est de reconnaître le mieux possible les 9 manuscrits, il semblerait que la valeur de k optimale soit 18.
Si notre but est de reconnaître le mieux possible les 9 manuscrits, il semblerait que la valeur de k optimale soit 18.
Algorithme des k-moyennes – Exemple d’apprentissage non supervisé
Le boulot de l’algorithme des k-moyennes (k-means) n’est pas d’étiqueter les données, mais de les regrouper par famille. C’est donc un algorithme de partitionnement des données (clustering).
Contrairement à KNN, l’algorithme des k-moyennes ne nécessite pas de données préétiquetées. Il fait ainsi parti des algorithmes d’apprentissage automatique non-supervisé (il se débrouille tout seul avec les données mystères).
Par contre, l’algorithme partage avec KNN sa grande simplicité d’emploi et son efficacité qui le rendent lui aussi très populaire dans l’industrie.
Principe
L’algorithme dépend d’un seul paramètre en plus des données : le nombre de partitions (clusters) k.
On commence par choisir k points au hasard dans l’espace des données (il peut s’agir de k points de données ou de k autres points). Ce sont les k centres (ou centroïdes).
Plus les points choisis au départ sont éloignés les uns des autres, mieux c’est. Une amélioration de l’algorithme de base proposée en 2007, k-means++, s’en assure.
On attribue ensuite à chaque centre tous les points de données qui lui sont le plus proches, formant ainsi k groupes.
Enfin, on déplace chaque centre au barycentre de son groupe.
On répète les deux dernières opérations (attribution des points les plus près et déplacement des centres) tant que les centres bougent d’une itération à l’autre.

L’algorithme vise à résoudre au final un problème d’optimisation ; son but est en effet de trouver le minimum de la distance entre les points à l’intérieur de chaque partition.
Mathématiquement, étant donné un ensemble de points $(x_1,x_2,\ldots,x_n)$, on cherche à partitionner les $n$ points en $k$ ensembles $S=\{S_1,S_2,\ldots,S_k\}$ en minimisant la grandeur : $$I = \sum_{i=1}^{k}\sum_{x_j \in S_i}||x_i-\mu_i||^2$$ où $\mu_i$ est le barycentre des points dans $S_i$.
$I$ est la variance intra-classe ou inertie intra-classe (terme surtout utilisé en anglais).
Choix de k
Choisir le bon nombre de clusters est crucial pour l’algorithme des k-moyennes, comme l’illustre l’exemple suivant :
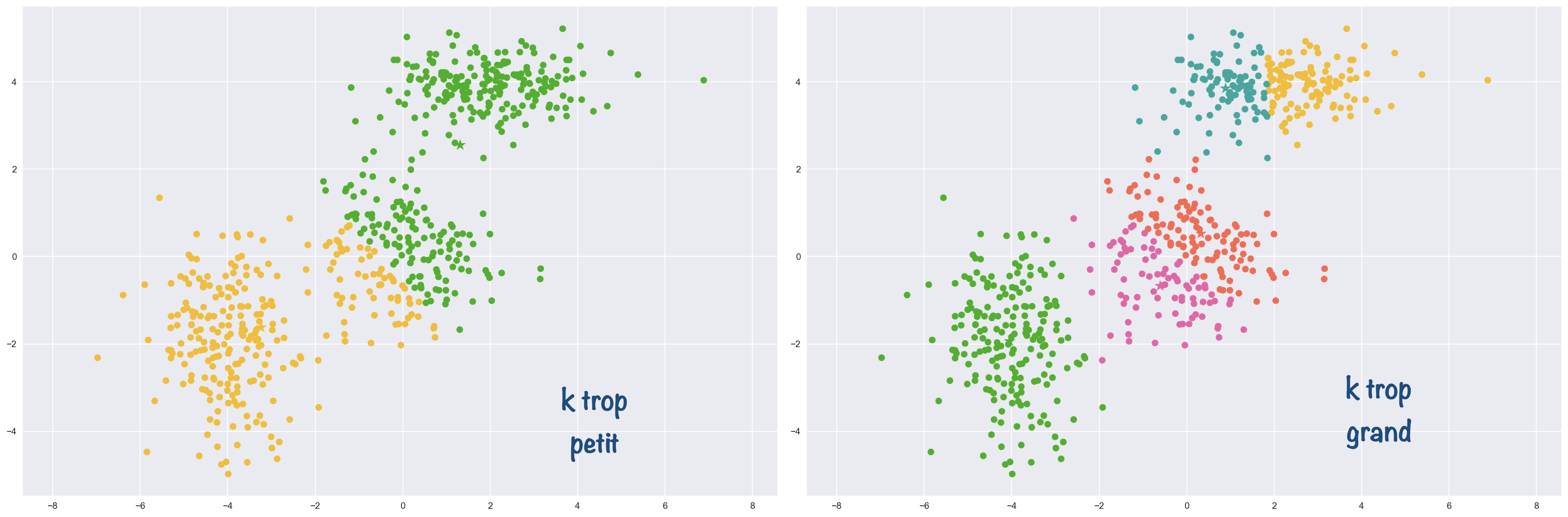
Mais ce n’est pas toujours simple (contrairement à l’exemple) de deviner le bon nombre de clusters juste en inspectant les données. Alors comment faire ?
On pourrait se dire qu’il suffit de prendre le modèle avec la plus faible inertie. Mais malheureusement, l’inertie n’est pas une métrique adaptée au choix de k puisqu’elle ne fait que descendre quand k augmente… Logique : plus il y a de clusters, plus la distance intra-cluster diminue !
Traçons l’inertie en fonction de k pour y voir plus clair :
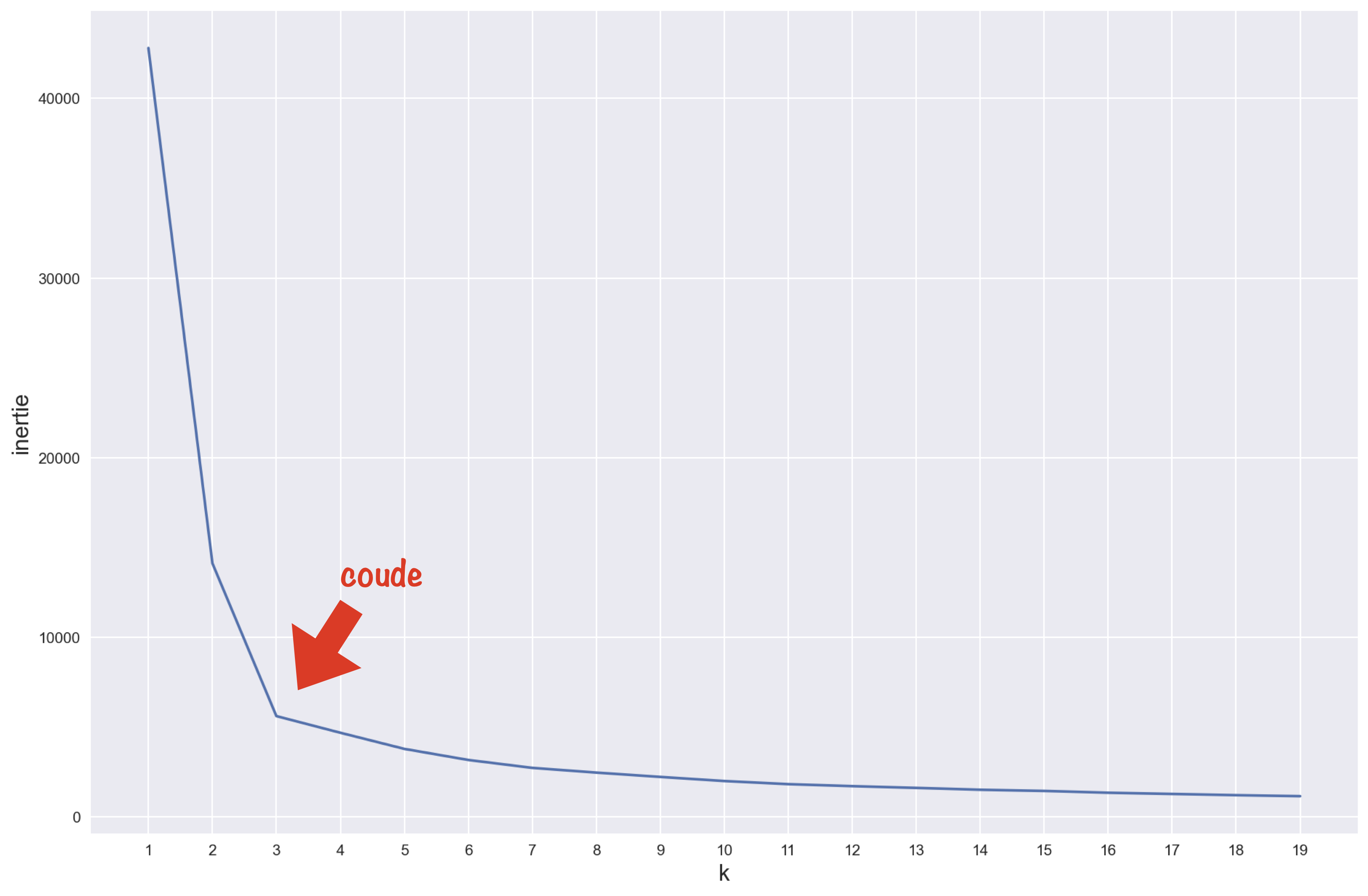
On remarque qu’ici, le nombre de clusters idéal correspond au point d’inflexion de la courbe (ou, si on imagine un bras, au coude).
Confirmons en simulant des données séparées en 5 tas et en retraçant la courbe.
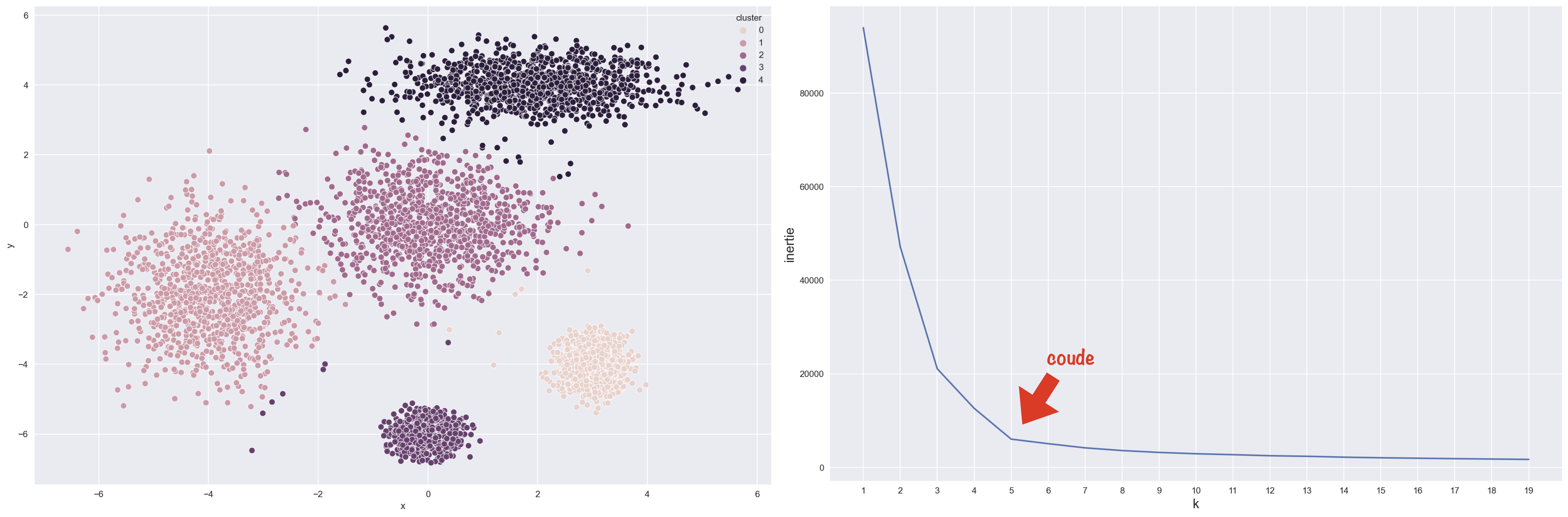
Là encore, le coude indique le nombre k idéal.
On semble donc avoir trouver une tactique utilisable lorsqu’on n’a pas d’autres indices.
Il existe des méthodes plus précises pour déterminer k, mais elles sont aussi plus gourmandes en calcul. La plus répandue utilise les coefficients de silhouette de chaque point (différence entre la distance moyenne avec les points du même groupe (cohésion) et la distance moyenne avec les points des autres groupes voisins (séparation)).

Limites
L’algorithme des $k$-moyennes se confronte à une difficulté classique en apprentissage automatique, et plus généralement pour tout problème d’optimisation : obtenir un minimum global plutôt qu’un minimum local.
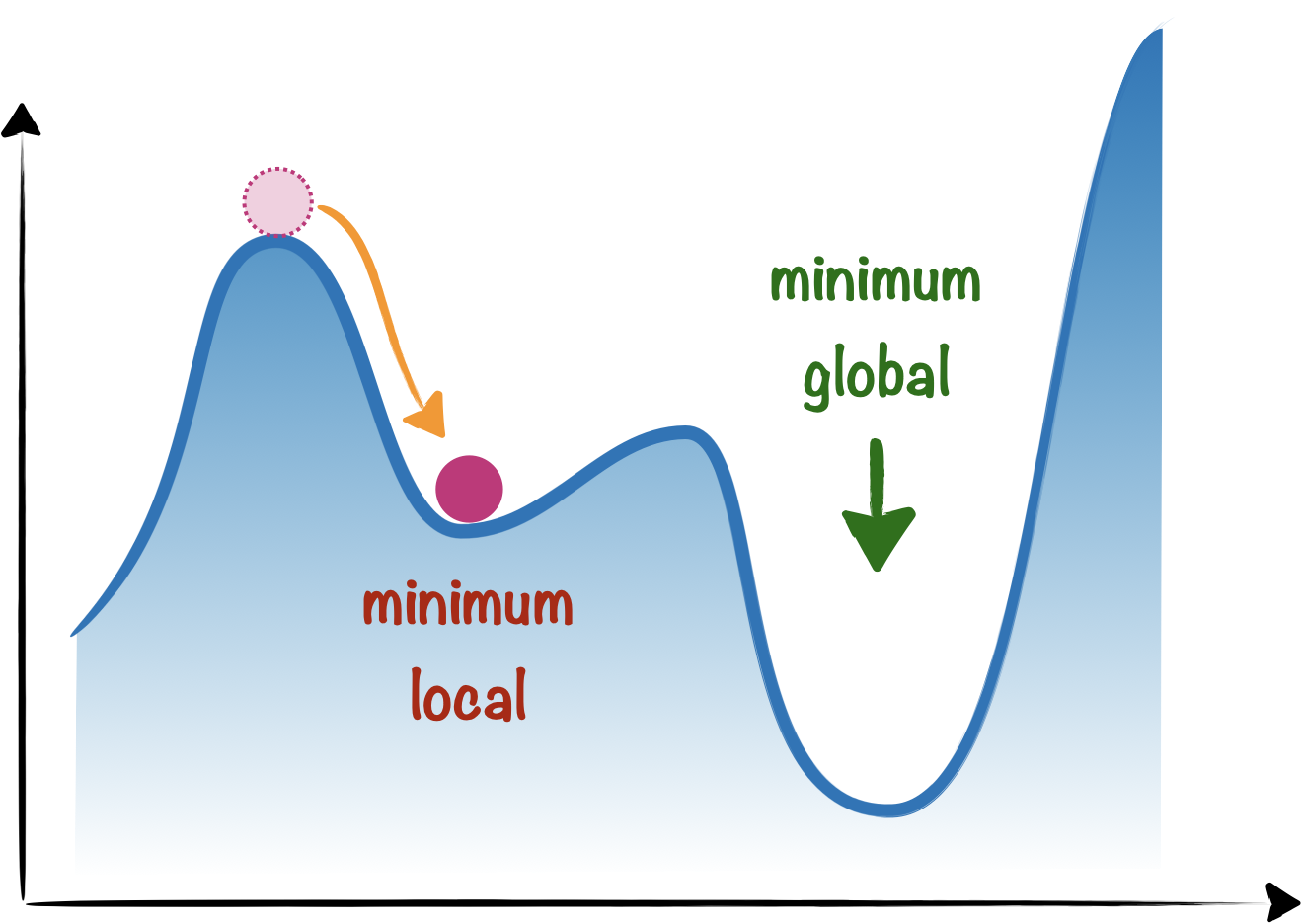
La convergence vers un des minima locaux dépend crucialement de la position initiale des centres.
Dans l’exemple suivant, on obtient 3 partitionnements différents pour 3 initialisations différentes des centres.
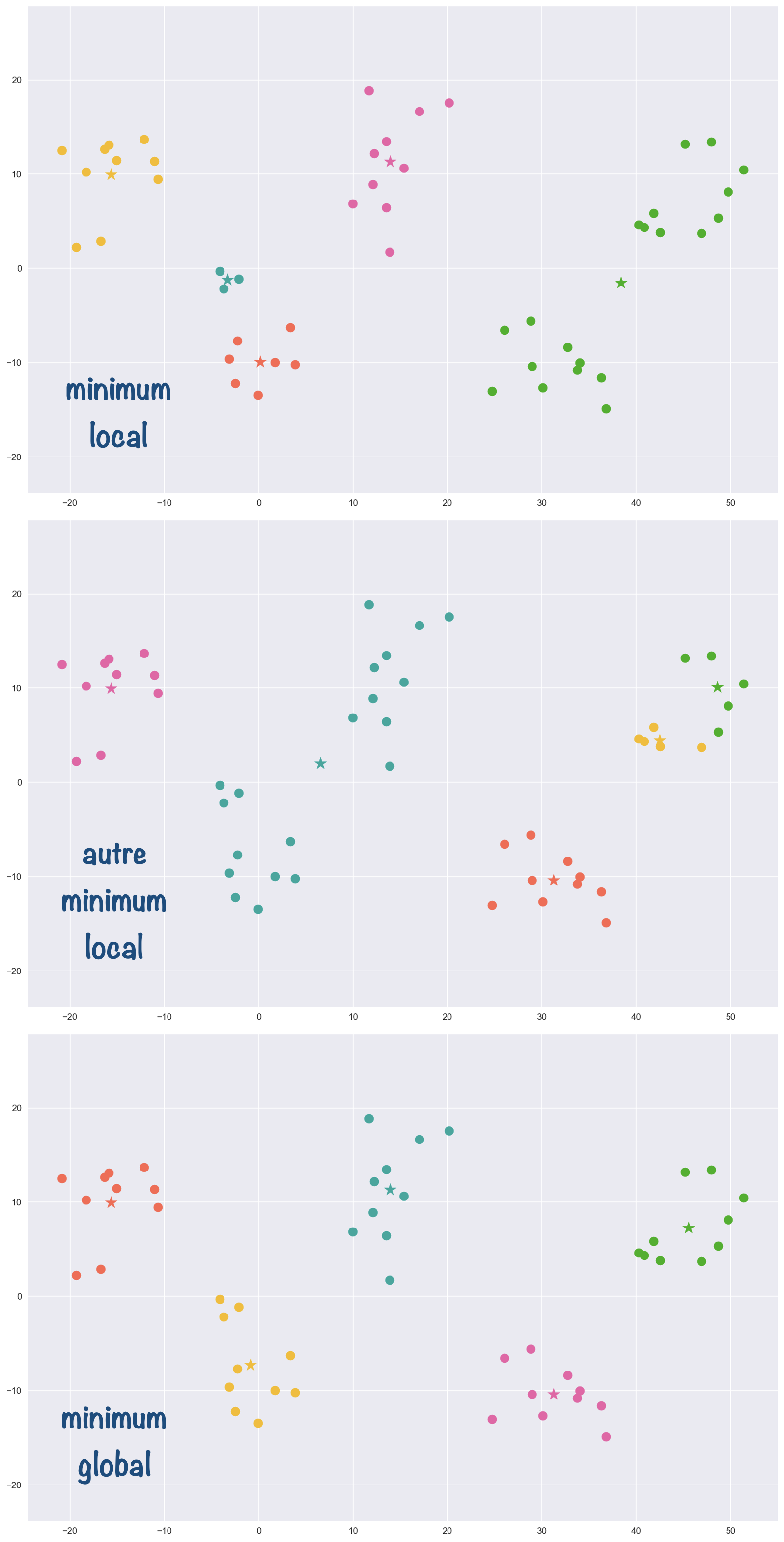
On vérifie que les centres sont bien bloqués sur leur position dans les deux premiers cas puisqu’aucun changement d’attribution n’est possible.
Dans l’algo classique, pour pallier au mieux ce problème, on initialise les centres aléatoirement et on relance l’algorithme un certain nombre de fois pour ne garder au final que la solution qui minimise l’inertie intra-classe.
Autre souci des k-moyennes : des difficultés pour partitionner des clusters de différentes tailles, différentes densités ou des formes non sphériques.
Applications
L’algorithme des k-moyennes ne présuppose rien sur les données et peut s’avérer, par le fait, très utile en première approche.
C’est bien ce rôle de défricheur qu’on a donné à l’algorithme dans le TP3 lors de l’analyse de l’enquête mondiale sur le bonheur pour créer des groupes de pays similaires et tenter de comprendre ce qui les rassemble.
L’algorithme permet aussi de trancher des débats de la plus haute importance sur les couleurs comme “est-ce plus vert que bleu ?” en organisant un combat entre les centroïdes de chaque couleur.
Dans la même veine, on peut utiliser k-moyennes pour segmenter une image par couleur (voir TP13), ce qui peut s’avérer intéressant pour des données satellite par exemple. Le choix de k correspond alors au nombre de couleurs qu’on veut garder.
L’exemple ci-dessous est issu du TP :

La simplicité de k-moyennes en fait un bon outil de dégrossissage des données, y compris sur des données déjà étiquetées. Cela permet de réduire leur dimensionnalité, avant d’utiliser des algorithmes plus complexes d’apprentissage supervisé.
Jeux d’accessibilité sur un graphe
Cette partie du cours a moins à voir avec les jeux vidéo qu’avec la modélisation de systèmes réactifs (automate bancaire, système-environnement), les problèmes de contrôle, la théorie de la décision, les problèmes de routage sur Internet, l’économie… Autant de domaînes admettant une description en terme d’opposition entre adversaires sur une arêne (un des adversaires pouvant modéliser l’environnement). La détermination d’une stratégie gagnante résout alors le problème posé en assurant sa correction.
L’arène
On entendra ici par jeu :
- des jeux à deux joueurs ($J_1$ et $J_2$ ou Eve et Adam)
- à information complète : les deux joueurs savent tout (pas comme aux cartes)
- alternés (pas comme à chifoumi)
- non randomisés (pas de hasard)
L’arène dans laquelle le jeu prend place est un graphe orienté biparti.
Un graphe biparti (ou bipartite) $G$ est un graphe dont l’ensemble des sommets peut être divisé en deux sous-ensembles de sommets disjoints $S_1$ et $S_2$ ($S_1$ et $S_2$ sont une partition de $S$ : $S_1\cup S_2=S$, $S_1\cap S_2=\varnothing$) tels que chaque arête de $G$ a une extrémité dans $S_1$ et l’autre dans $S_2$.

Un graphe est biparti si on peut colorier tous les sommets du graphe avec seulement deux couleurs de manière à ce que deux sommets voisins n’aient jamais la même couleur (on parle alors de 2-coloriage).
On peut montrer qu’un graphe est biparti si et seulement si il ne possède pas de cycle de longueur impaire.
Démonstration de “graphe biparti $\Leftrightarrow$ pas de cycle impair” :
On montre $\Rightarrow$ en constatant l’impossibilité d’un 2-coloriage sur un cycle impair. Donc tout graphe contenant un cycle impair ne peut pas être biparti.
Et on montre $\Leftarrow$ en essayant de créer un 2-coloriage depuis un sommet ; tant qu’on ne rencontre pas de cycle, pas de problème.
Tous les sommets à une distance impaire du sommet de départ sont coloriés d’une couleur et tous ceux à une distance paire sont coloriés de l’autre couleur.
Donc un graphe sans cycle est toujours biparti.
Place aux cycles maintenant. Supposons que deux des chemins partant d’un sommet se rejoignent, alors on a deux possibilités :
- la jonction se fait entre deux sommets de couleurs différentes et le 2-coloriage reste possible.
Dans ce cas, on joint un chemin de longueur pair et un chemin de longueur impair, ce qui donne un cycle de longueur pair (avec le +1 de l’arête de la jonction).- la jonction se fait entre sommets de la même couleur rendant impossible le 2-coloriage.
Dans ce deuxième cas, on obtient nécessairement un cycle de longueur impaire puisqu’on joint deux chemins de la même parité (+ 1 de l’arête de jonction).Seuls les cycles impairs font donc échouer le 2-coloriage. Tout graphe non biparti contient au moins un cycle impair.
Retournons aux jeux…
Deux joueurs, $J_1$ et $J_2$, s’affrontent sur un graphe orienté biparti $G=(S,A)$ où $S$ est constitué des sommets contrôlés par le joueur 1, $S_1$, et de ceux contrôlés par le joueur 2, $S_2$. Chaque sommet est une position valide du jeu et chaque arête est un mouvement autorisé entre ces positions.
Il manque encore une condition de gain pour rendre le jeu intéressant ; dans le cas d’un jeu d’accessibilité, on attribue à chaque joueur un sous-ensemble de sommets correspondant à des états gagnants qu’il convient d’atteindre pour… gagner. Il peut aussi exister un sous-ensemble de sommets correspondant à des états de partie nulle.
Un jeu d’accessibilité est alors défini par un quadruplet $(G,S_1,S_2,F)$ où $(G,S_1,S_2)$ est une arène et $F$ est l’ensemble des sommets gagnants pour $J_1$.
Exemples
Chomp
Chomp est un jeu où les deux adversaires mangent à tour de rôle des carrés de chocolat d’une tablette avec la “contrainte” de manger tous les carrés à droite et au-dessus du carré choisi. Le perdant doit manger le brocoli qui reste à la fin.
Eve commence le jeu avec la tablette ci-dessous composé de 5 carrés. Il existe alors 9 configurations possibles, pas toutes atteignables par les deux joueurs.
Traçons l’arène (les ronds bleus sont les positions contrôlées par Eve et les carrés roses par Adam).
$F$ (sommet gagnant pour Eve) est le carré rose avec un brocoli puisque l’atteindre signifie qu’Adam se retrouve avec le légume à manger.

Une des nombreuses variantes du jeu de Nim
Un tas d’allumettes est disposé devant Eve et Adam. Eve joue en premier et peut retirer autant d’allumettes qu’elle le souhaite du moment qu’elle en prend au moins une et qu’elle en laisse au moins une. C’est ensuite au tour d’Adam de retirer des allumettes avec pour tous les tours qui suivent une contrainte supplémentaire : on ne peut pas retirer plus de deux fois le nombre d’allumettes prises par son adversaire au tour précédent. Le joueur qui retire la dernière allumette gagne. Il n’y a pas de match nul.
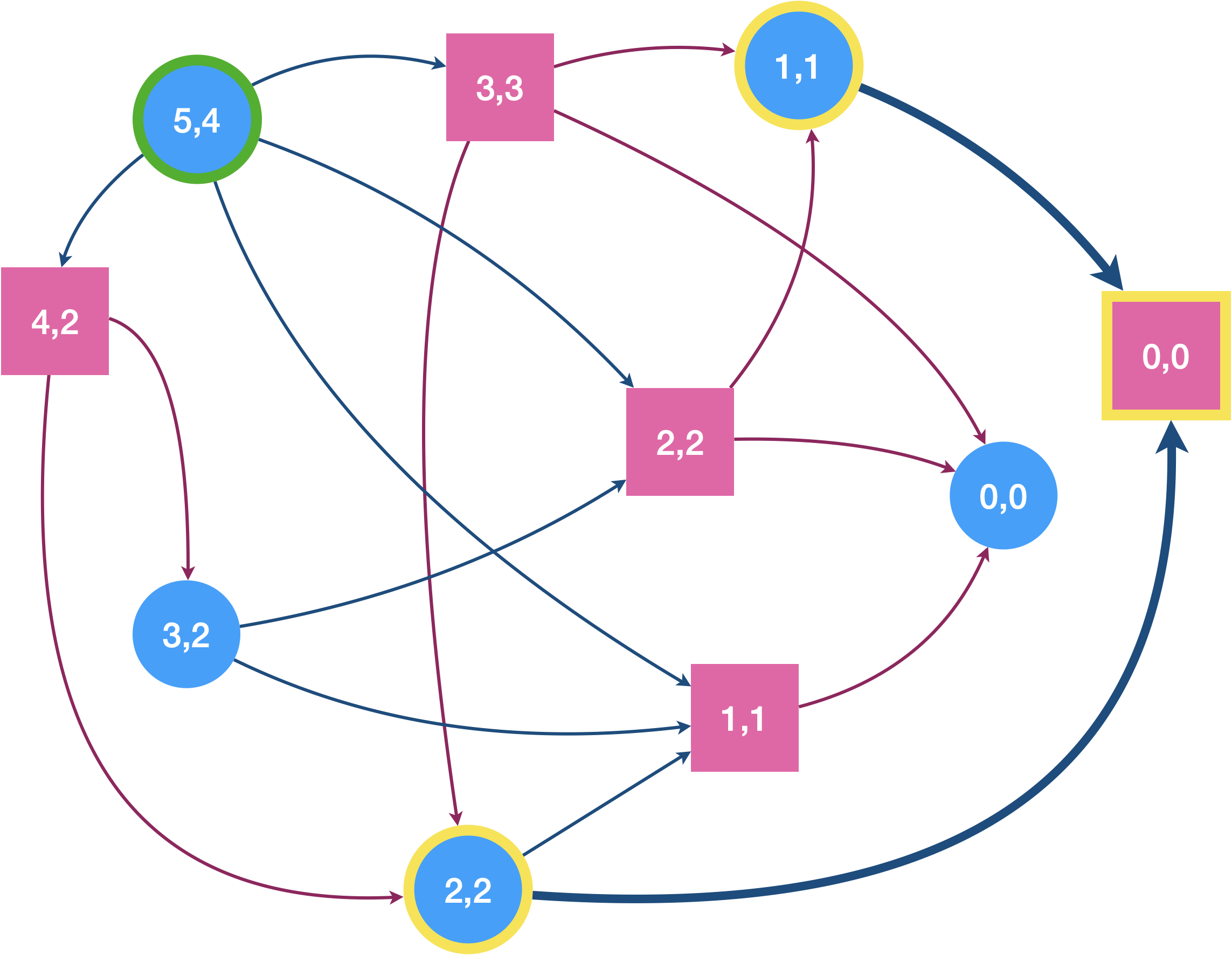
Traçons le graphe du jeu en supposant que l’on commence avec 5 allumettes et étiquetons les sommets avec le couple (nombre d’allumettes présentes, nombres d’allumettes prenables). L’étiquette du nœud de départ est donc (5,4).
On a indiqué en jaune le sommet à atteindre pour Eve (sommet de $F$).
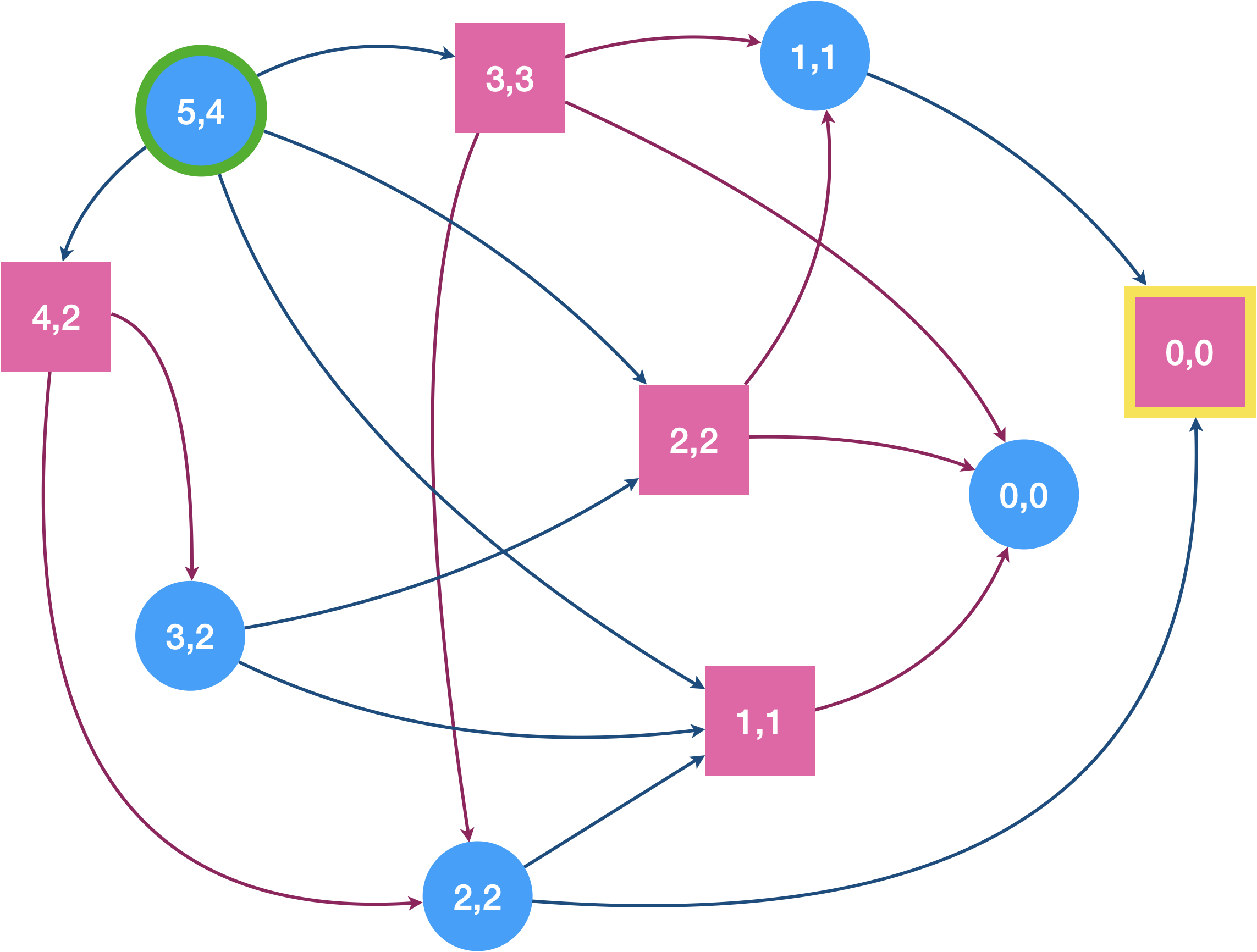
Le graphe est ici plutôt simple, mais on verra dans le TP que pour des nombres d’allumettes plus grand, on sera content de pouvoir confier la tâche de sa construction à python.
Ce jeu est une variante du jeu de Nim (voir TP) comme en fait tout jeu impartial à deux joueurs (théorème de Sprague-Grundy). Un jeu impartial est un jeu tour par tour dans lequel les coups autorisés, ainsi que les gains obtenus, dépendent uniquement de la position, et pas du joueur dont c’est le tour. C’est le cas de Chomp qui est donc, lui aussi, un jeu de Nim déguisé… Un jeu qui n’est pas impartial est appelé jeu partisan (le morpion ou les échecs par exemple).
Morpion (tic-tac-toe)
Pas besoin de rappeler les règles du morpion (oxo en belgique).
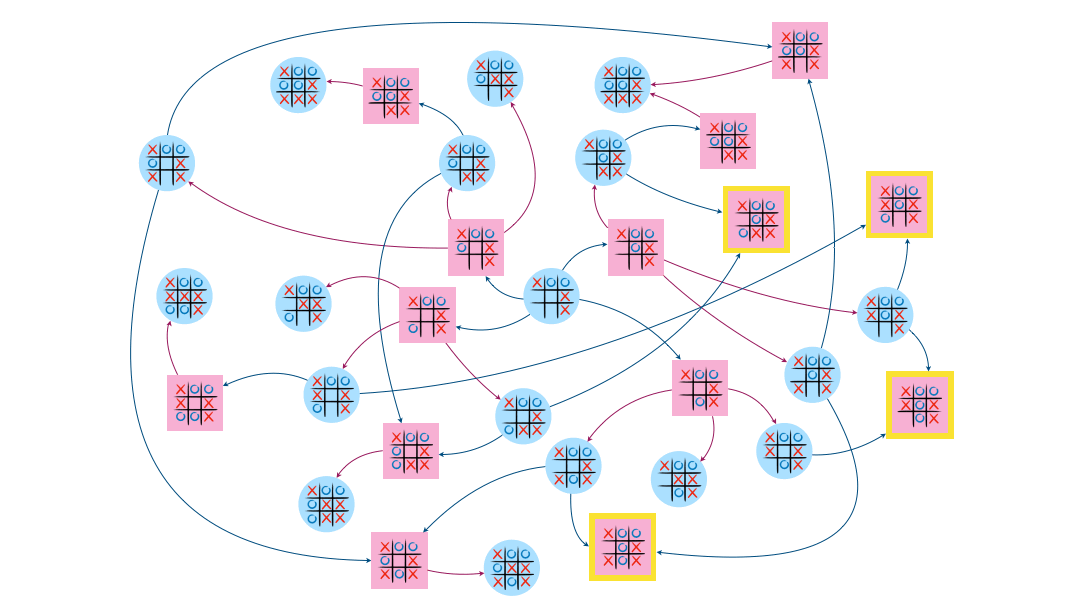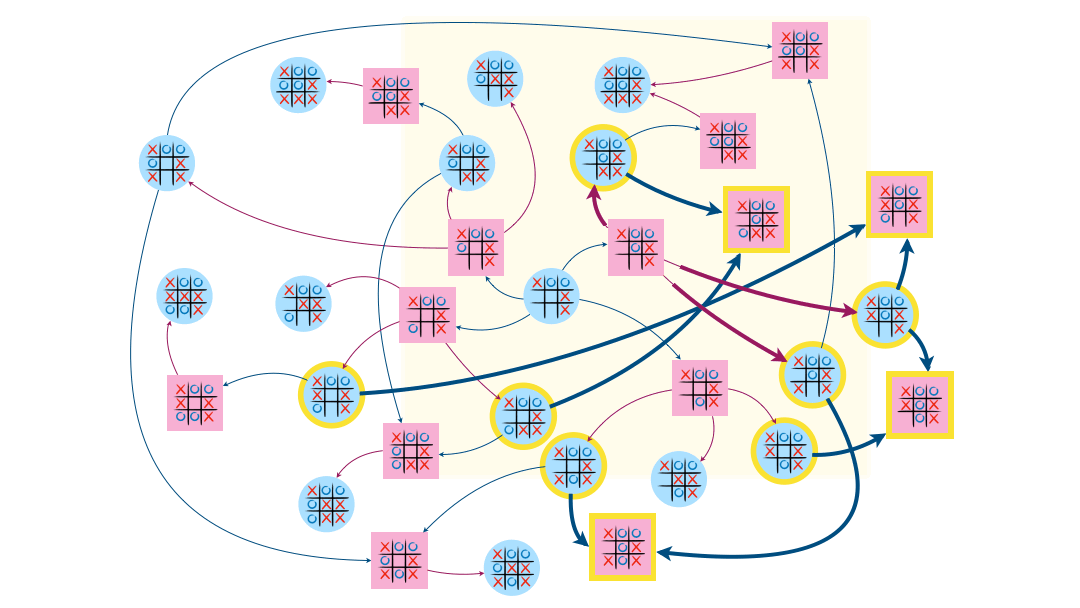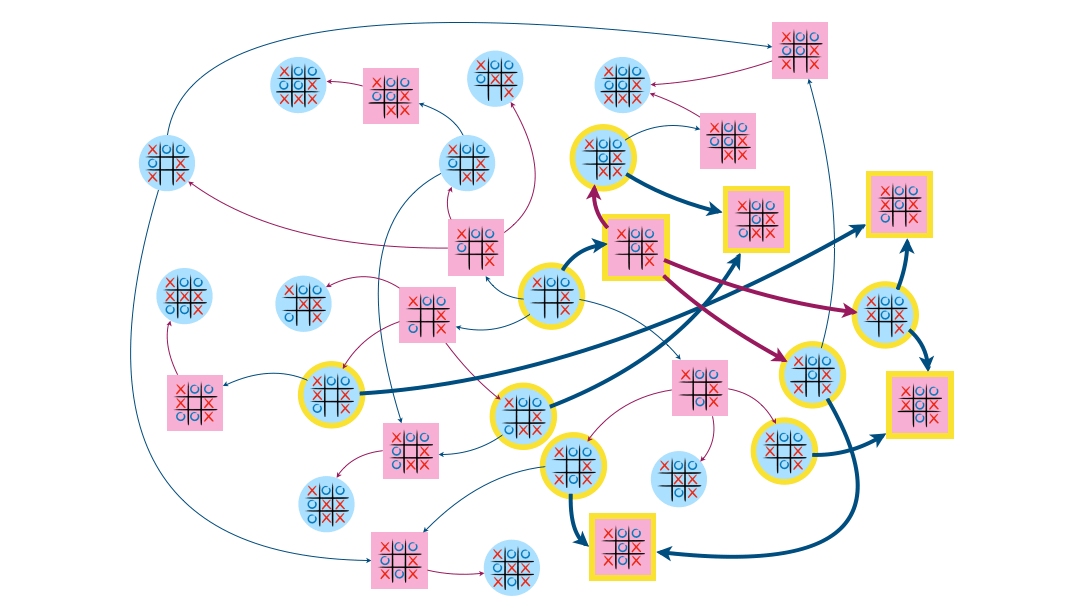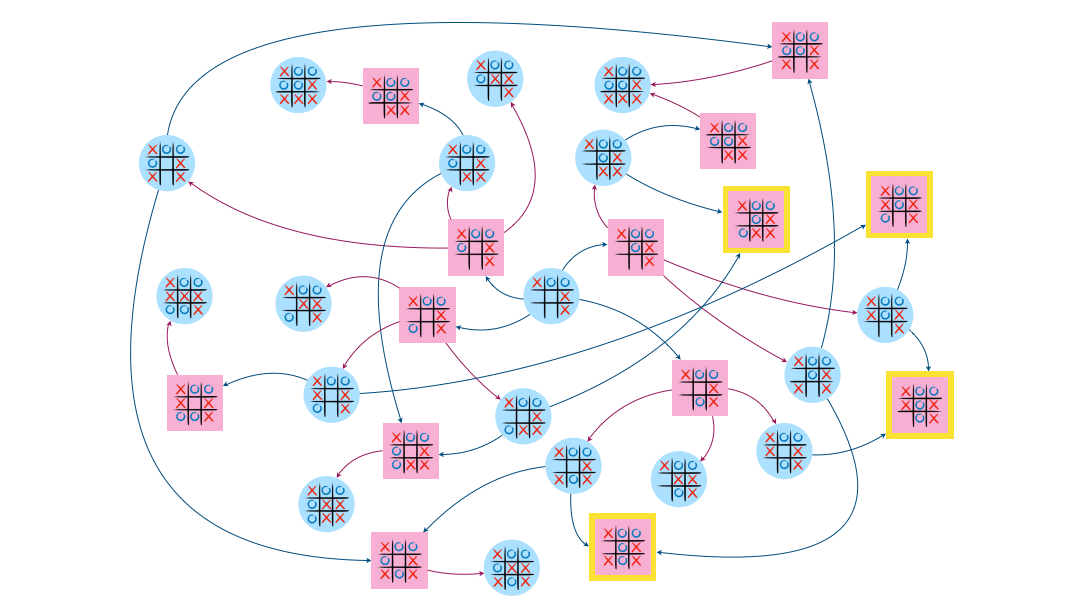
Dans cet exemple, Eve démarre sur un jeu déjà avancé, elle a les ronds.
Cette fois-ci, $F$ contient plusieurs sommets (toujours indiqués en jaune).
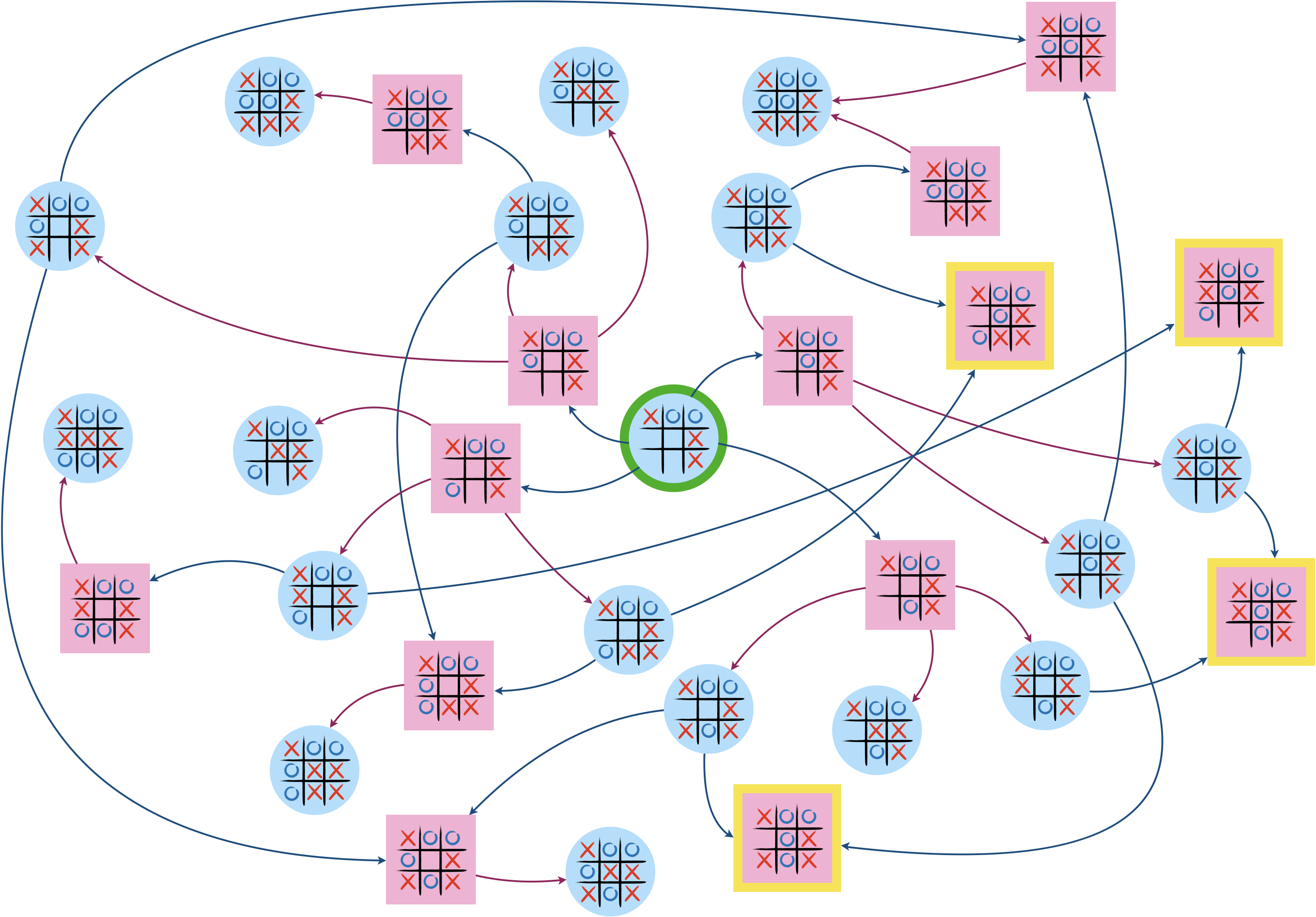
Stratégie
Gagner la partie, c’est arriver sur un sommet de $F$. Comment savoir si Eve peut ou non gagner selon sa position de départ ? Et si elle le peut, comment mettre au point pour elle une stratégie gagnante ?
Positions gagnantes et attracteurs
Pour déterminer l’ensemble des positions gagnantes pour Eve sur l’arène, on travaille récursivement depuis les sommets de $F$ en suivant les deux préceptes suivants :
- un sommet d’Eve est gagnant si un de ses arcs sortants le lie à un sommet gagnant.
Eve n’a alors plus qu’à emprunter ce chemin.
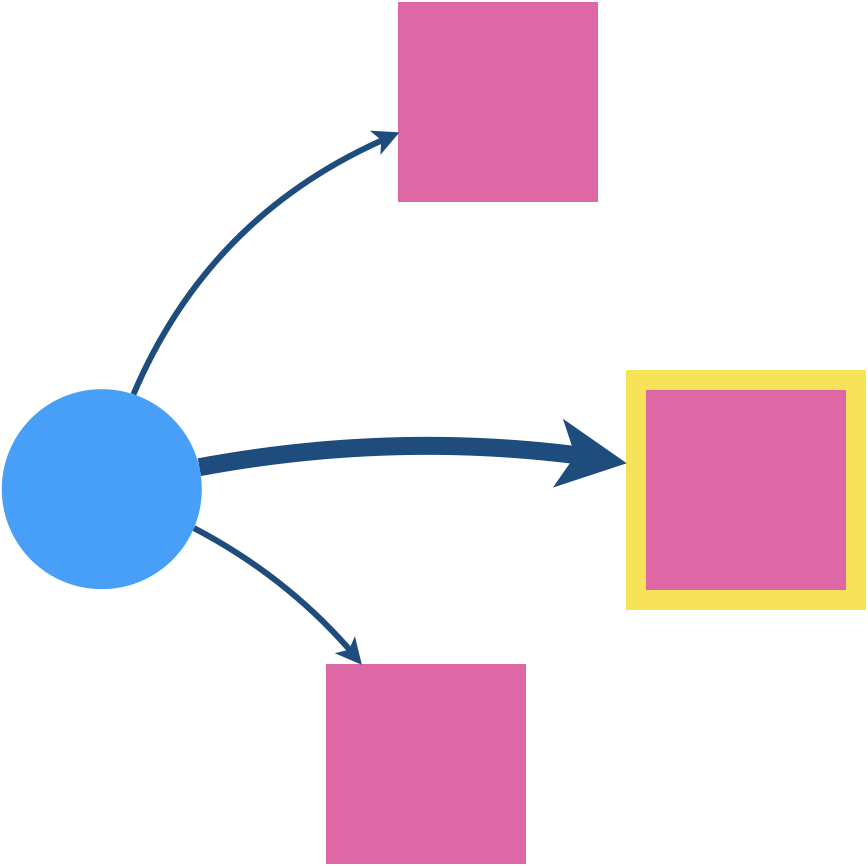
- un sommet d’Adam est gagnant (pour Eve) si tous ses arcs sortants le lie à un sommet gagnant.
En effet, Adam ne peut alors pas éviter de mettre Eve dans une position gagnante.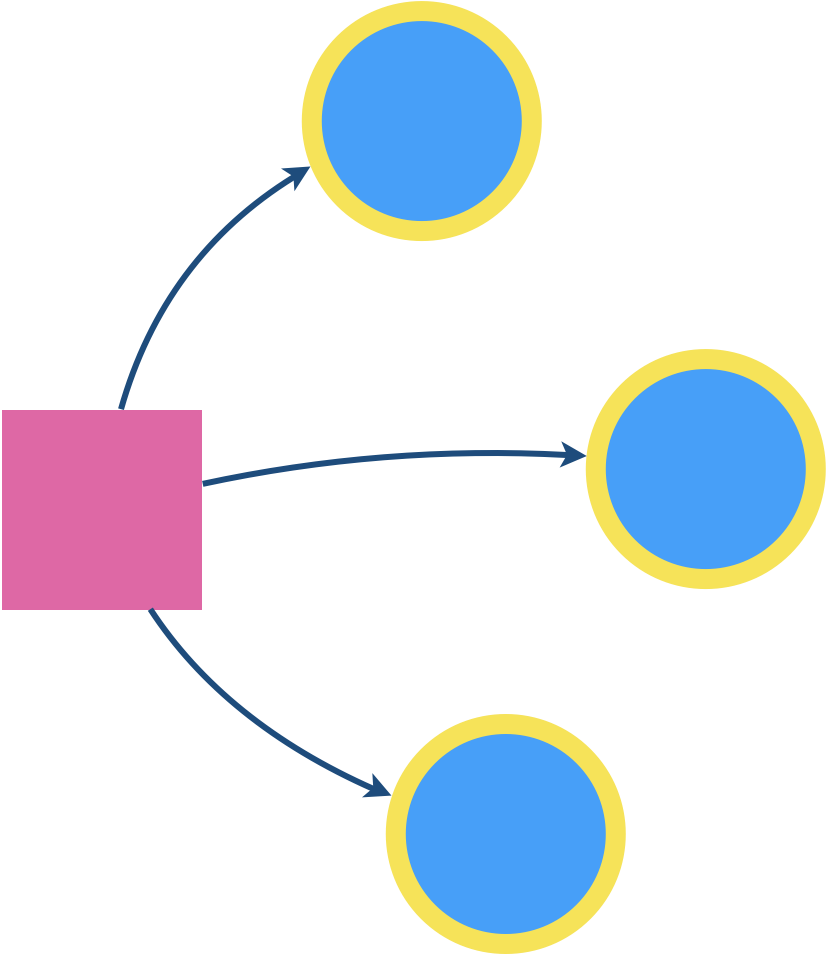
Formalisons un peu tout ça en définissant la suite $Attr_i(F)$ qui contient l’ensemble des sommets gagnants après $i$ étapes : $$ \begin{array}{lll} Attr_0(F) &= &F \\ Attr_{i+1}(F) &= &Attr_{i}(F) \\ &&\cup \{s \in S_1|Succ(s)\cap Attr_i(F) ≠ \varnothing \} \\ &&\cup \{s\in S_2| Succ(s)\subseteq Attr_i(F)\} \end{array} $$ Étant donné que $Attr_i(F) \subseteq Attr_{i+1}(F) \subseteq S$, pour tout $i≥0$, si on suppose le graphe fini, la suite est croissante et bornée et donc stationnaire (à partir d’un certain $i=i_0$, $Attr_i(F)$ est constante, et si $|G|=n$, $i_0$ vaut au plus $n-1$).
On appelle attracteur de $F$ pour le joueur $J_1$ la limite de $Attr_i(F)$. On le note $Attr(F)$.
Tout sommet dans l’attracteur est une position gagnante pour $J_1$.
Le complémentaire d’un attracteur est appelé piège. Si le joueur 1 est sur une position n’appartenant pas à son attracteur (et donc à son piège), cela signifie que :
- si c’est son tour, tous les mouvements possibles restent dans le piège,
- si c’est le tour de l’adversaire, celui-ci a toujours au moins une possibilité de laisser le joueur 1 dans le piège.
Cette position est donc perdante…
Détermination “à la main” de l’attracteur dans les exemples précédents
L’attracteur dans l’exemple du jeu Chomp contient 9 sommets, dont le somme de départ.
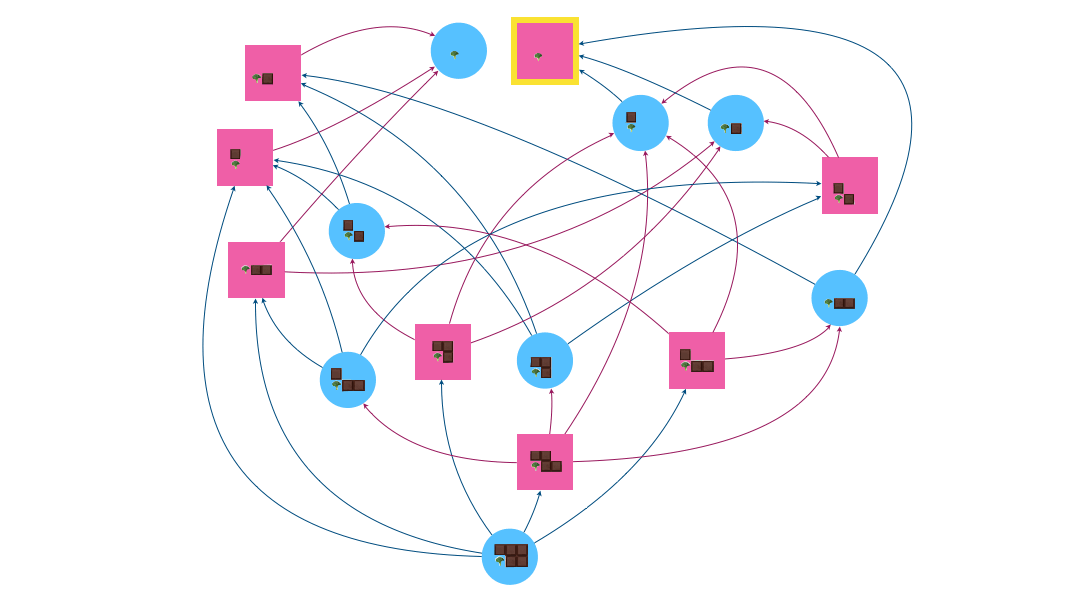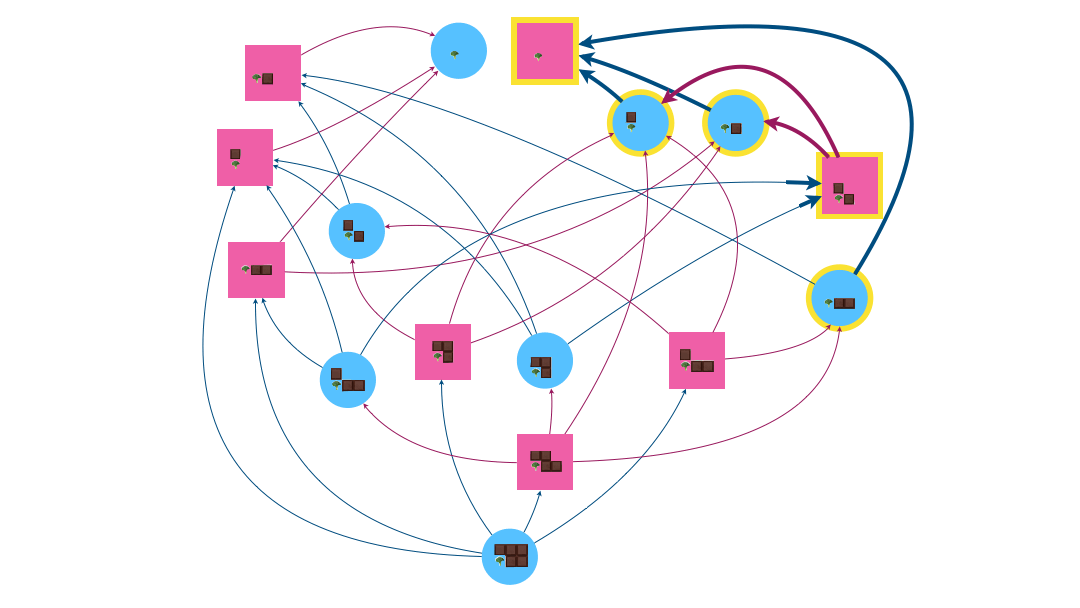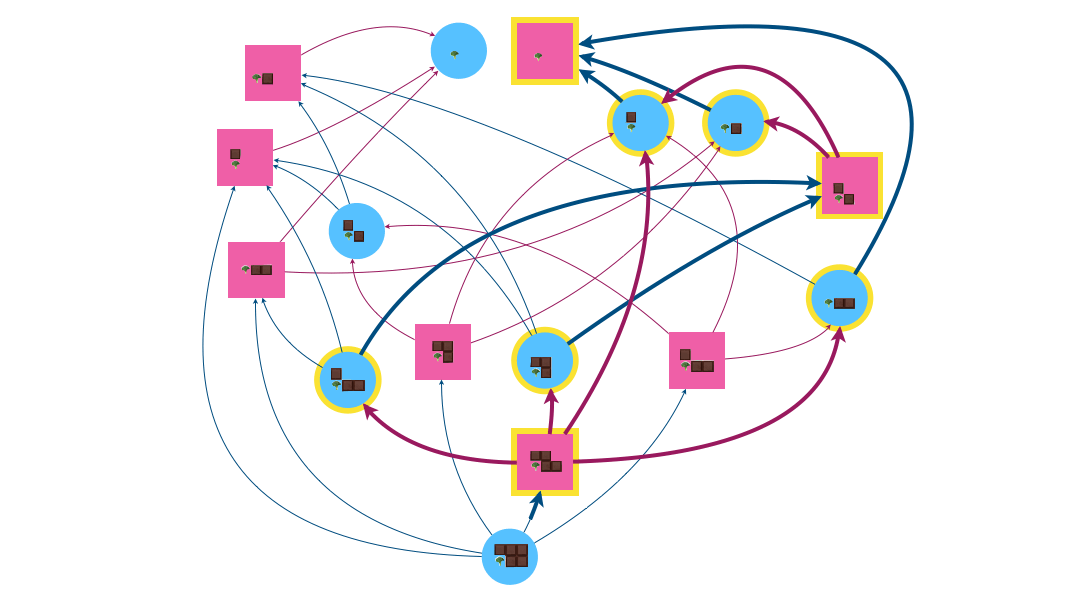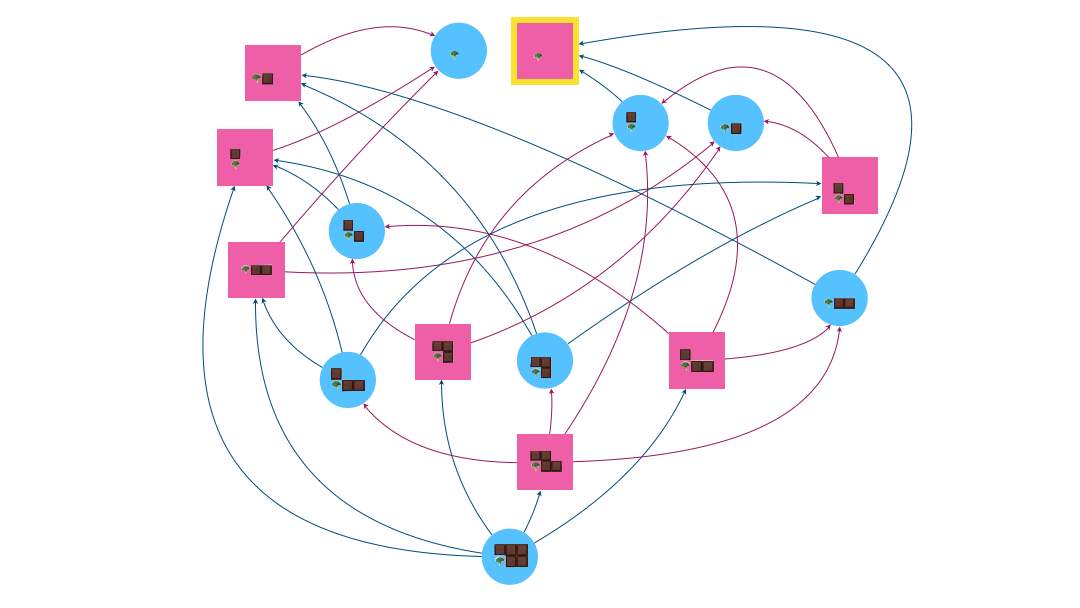
Dans le cas de la variante de Nim, l’attracteur se réduit à $Attr(G) = \{(0,0,1) , (1,1,0) , (2,2,0) \}$ où la troisième valeur des triplets correspond au joueur qui contôle le sommet (0 pour Eve et 1 pour Adam). Le sommet de départ $(5,4,0)$ n’est pas dedans $\Rightarrow$ c’est perdu pour Eve 😭..
Enfin, sur l’exemple du morpion, l’attracteur contient 13 sommets dont celui de départ.
Programme permettant de calculer l’attracteur
On peut écrire un programme récursif calculant l’attracteur en temps linéaire en $|S | + |A|$ (rappelons-nous que le parcours complet d’un graphe est au mieux en $O(|S | + |A|)$ car cela correspond à parcourir les $|S|$ sommets et les $|A|$ arêtes). Pour éviter de calculer plusieurs fois le même élément, l’algorithme tient à jour, pour chaque sommet $s$, un compteur n des successeurs non encore inspectés (sous la forme d’un dictionnaire) .
def attracteur(G: dict, F: list) -> list:
"""
préconditions: G est est un graphe sous forme de liste d'adjacence implémentée par un dictionnaire
F est la liste des sommets gagnants pour le joueur 1
postcondition: la fonction retourne l'attracteur de F pour le joueur 1 sous forme d'un dictionnaire
dont les clés sont les sommets de G et les valeurs True ou False suivant que le sommet appartienne ou non à l'attracteur
"""
Pred = inverseGraphe(G)
n = {s:len(G[s]) for s in G}
Attr = {s:False for s in G}
for sommet in F:
Joueur1 = True
propage(sommet,Joueur1,Attr,Pred,n)
return Attr
def propage(sommet,Joueur1,Attr,Pred,n):
if Attr[sommet]:
return
Attr[sommet] = True
for s in Pred[sommet]:
n[s] -= 1 # un successeur de s en moins
if Joueur1 or (n[s] == 0) :
propage(s,not Joueur1,Attr,Pred,n)
Stratégie gagnante
Une stratégie sans mémoire est une fonction $\sigma$ qui assigne un mouvement autorisé à un joueur pour chaque position non terminale : $\forall s\in S, (s,\sigma(s))\in A.$
Un joueur sur une position $s$ suit une stratégie s’il emprunte le chemin $<s,\sigma(s),\sigma^2(s),\ldots>$. Elle est dite sans mémoire car pour une position donnée, la stratégie est indépendante du chemin qui y a mené ($\sigma$ ne dépend que du sommet).
Une stratégie sans mémoire gagnante depuis une position donnée garantit la victoire au joueur en un nombre de coups limité. Pour le joueur 1, une stratégie gagnante garantit d’arriver sur un sommet de $F$. Mais suivant la position de départ, une telle stratégie n’existe pas forcément…
En construisant l’attracteur, on répond à notre première question : la position d’Eve est-elle gagnante ? Il suffit de vérifier qu’elle appartient à l’attracteur.
Si c’est le cas, une stratégie gagnante est facile à mettre en place ; il faut faire en sorte que chaque déplacement sur le graphe (chaque coup joué) se fasse vers un sommet de l’attracteur. Chaque coup d’Eve vers un sommet de l’attracteur piège aussi le coup suivant d’Adam dans l’attracteur.
Comme son nom l’indique, l’attracteur attire irrémédiablement vers $F$, assurant la victoire au joueur 1.
Le joueur 2 aussi, bien sûr, a son attracteur, et il appartient au complémentaire de l’attracteur du joueur 1, piège du joueur 1. Donc un seul écart du joueur 1 en dehors de son attracteur, et s’en est fini pour lui, le joueur 2 peut le condanner à rester dans le piège.

Revenons à nos exemples :
- Pour Chomp, le joueur 1 appartient à l’attracteur, ce qui signifie que sa position de départ est gagnante. Par conséquent, il a une stratégie gagnante. Mais attention à ne pas se tromper au début ! Sur 5 mouvements possibles, le seul assurant la victoire est de manger le carré en haut à droite.
- Pour la variante de Nim, c’est foutu… Quelle que soit notre stratégie, elle sera perdante.
- Enfin, pour Tic-tac-toe, la victoire tend les bras au joueur 1. Et, sans surprise, son premier mouvement doit être de prendre le milieu.
Arbre et minimax
Pour des jeux comme les échecs, le graphe est bien trop gros pour pouvoir appliquer nos méthodes précédentes. Alors comment s’en sortir ?
L’idée est de se contenter d’une recherche partielle autour de la position actuelle donnant à l’algorithme seulement quelques coups d’avance. Il évalue alors les différentes positions futures possibles en leur attribuant un score issu d’une heuristique.
Une heuristique est une méthode de calcul qui fournit rapidement une solution réalisable, pas nécessairement optimale ou exacte, pour un problème d’optimisation difficile. Elle s’impose quand les algorithmes de résolution exacte sont impraticables, à savoir de complexité polynomiale de haut degré, exponentielle ou plus.
Une heuristique est donc un compromis entre d’un côté l’optimalité (trouver la meilleure solution) et/ou la complétude (trouver toutes les solutions) de l’algorithme et de l’autre côté sa vitesse.
Pour implémenter efficacement cette recherche partielle, l’idée est d’utiliser un arbre plutôt que l’arêne précédente. Quelle différence ? L’absence de cycle qui va permettre d’élaguer ! On le paye au prix de la redondance des sommets (le même sommet peut apparaître plusieurs fois dans l’arbre). Pour chaque position, les différents coups possibles correspondent aux différentes branches et on avance ainsi niveau par niveau jusqu’aux feuilles représentant les positions terminales.
Le gros avantage d’un arbre est qu’il permet facilement de ne garder que quelques niveaux (on raccourci alors toutes les branches jusqu’à la profondeur considérée).
Muni de cet arbre, l’algorithme se lance dans un parcours en profondeur jusqu’à la profondeur maximale stipulée. Lorsque ce niveau est atteint (2, par exemple, si on veut que l’IA ait deux coups d’avance), l’algorithme évalue les feuilles grâce à son heuristique, puis il propage ce score vers les niveaux supérieurs en suivant le principe du minimax :
- sur un niveau correspondant au joueur 1, on sélectionne la valeur maximale parmi les branches,
- et sur un niveau correspondant à l’adversaire, on sélectionne la valeur minimale.
Le pricipe est de maximiser les gains du joueur 1 tout en minimisant ceux du joueur 2. La valeur est au final transmise à la racine (la position depuis laquelle on a lancé la recherche) et la meilleure branche est sélectionnée.
Prenons l’exemple du jeu de Morpion. Une heuristique possible pour évaluer un plateau pourrait consister à compter $+1$ pour chaque alignement encore possible pour le joueur et $-1$ pour ceux encore possibles pour son adversaire.

L’arbre total du morpion n’est pas si gros ; le facteur de ramification $b$ est de 5 en moyenne et il y a au plus 9 niveaux (9 coups), ce qui donne $\approx 5^9 = 1\,953\,125$ (à titre de comparaison, aux échecs, $b\approx35$ et un partie dure en moyenne 100 coups, ce qui donne $b^m\approx10^{54}$ sommets à inspecter…).
L’algorithme minimax appliqué au morpion inspecte en réalité environ 4 fois moins de sommets que les deux millions prédits, car ce chiffre ne tient pas compte des nombreuses parties potentielles se terminant avant le neuvième coup. Il en inspecte néanmoins beaucoup plus qu’il ne faudrait (il n’y a que $9!=362\,880$ coups possibles si l’ordi commence et seulement $8!=40\,320$ si l’humain a l’honneur), ce qui illustre le fait qu’un arbre contient beaucoup de sommets redondants par rapport au graphe du jeu dont il est tiré (c’est le prix à payer pour casser les cycles).
La taille modéré de l’arbre permet de l’explorer jusqu’aux parties finales, mais on peut constater en jouant avec le petit programme ci-dessous que la réduction à une profondeur d’un seul niveau grâce à l’heuristique2 est tout autant redoutable en inspectant presque 4000 fois moins de sommets !
Cela prouve qu’au morpion, 1 coup d’avance, c’est bien suffisant… Mais ce n’est pas vraiment le cas aux échecs, où les plus grands joueurs (comme Kasparov) prévoient jusqu’à 12 coups à l’avance ! Deep Blue, qui a battu Kasparov en 1997, cherchait jusqu’à une profondeur typiquement comprise entre 6 et 16, mais pouvait aller jusqu’à 40 dans certaines situations.
Dans le cas des échecs, l’heuristique permettant d’évaluer un état de l’échiquier est bien plus complexe qu’au morpion. Elle doit prendre en compte la quantité de pièces et pions restants, la qualité des pièces et les positions de tout ce beau monde (domination du centre, structure compacte, etc.).
La taille du jeu de Go rend vaine toute tentative de type minimax. C’est au point que les grands joueurs de Go ont longtemps refusé de jouer contre des ordinateurs, non par peur de perdre, mais parcequ’ils les trouvaient trop mauvais. C’est l’essor du deep learning, et donc une philosophie basée sur l’apprentissage plus que sur la stratégie, qui a permis à la machine de devenir un adversaire coriace à ce jeu-là aussi.
Sac à dos et heuristique
Voyons enfin une autre utilisation d’heuristique avec le problème du sac à dos, ici dans sa version “0/1” (knapsack 0/1 en anglais).
Le problème du sac à dos est un problème classique d’optimisation avec d’importantes applications théoriques et industrielles.
Soit $x\in\mathbb{N}^{*}$, soit $v$ une séquence de $n$ éléments appartenant à $\mathbb{N}^{*}$, et soit $p$ une séquence de $n$ éléments appartenant à $\{1,2,…,c\}$.
Nous appelons $c$ la capacité, $v$ la séquence de valeurs et $p$ la séquence de poids.
Le problème du sac à dos consiste à mettre des objets de poids $p$, dans un sac à dos qui peut contenir un poids maximal $c$, de telle sorte que la valeur des objets choisis est maximisée.
Plus formellement, cela revient à maximiser
$$\text{val}(x)=\sum_{i=1}^n x[i]\cdot v[i]$$
sous la contrainte $c≥\sum_{i=1}^n x[i]\cdot p[i]$, où $x\in\{0,1\}^n$ indique les objets choisis.
Exemple : supposons que le sac ait une capacité de 900 et que l’on cherche à y placer les objets suivants
| objets | 🥏 | 🎺 | 🥊 | 🧸 | 🪠 | ⏰ |
|---|---|---|---|---|---|---|
| valeurs $v$ | 5 | 50 | 65 | 20 | 10 | 12 |
| poids $p$ | 320 | 700 | 845 | 180 | 70 | 420 |
Le plus simple pour arriver à nos fins est de suivre une stratégie gloutonne (une stratégie étape par étape où un critère de classement permet de sélectionner le prochain objet à ajouter). Un critère qui semble prometteur est le ratio valeur/poids de chaque objet. L’idée est alors de placer les objets dans le sac dans l’ordre inverse de leur ratio. Cela semble une bonne stratégie puisque les objets ajoutés maximisent ainsi la valeur qu’ils apportent par rappor à la place qu’ils prennent. Mais si l’approche gloutonne a l’avantage d’être très simple, le revers de la médaille est qu’elle est à courte vue, on perd la vision d’ensemble. Et dans certaines configurations, comme c’est le cas dans notre exemple, cela s’avère contre-productif.
| objets | 🥏 | 🎺 | 🥊 | 🧸 | 🪠 | ⏰ |
|---|---|---|---|---|---|---|
| ratio $v/p$ | 1/64 | 1/14 | 1/13 | 1/9 | 1/7 | 1/35 |
L’approche gloutonne nous encourage ici à placer d’abord 🪠 dans le sac, puis 🧸, et c’est tout. Plus de place pour l’objet suivant (🥊). On obtient finalement une valeur de 30 et un poids de 250.
Cet exemple nous montre que l’approche gloutonne ne garantit pas l’optimalité (loin de là même, vu la place qu’il reste dans le sac…). On pourrait néanmoins facilement améliorer les choses en continuant d’essayer de placer les éléments de ratio plus grand sans s’arrêter au premier blocage. On tente 🎺, trop grosse, puis ⏰, là ça rentre, et enfin 🥏 qui ne loge pas. On obtient ainsi une valeur de 42 et un poids de 670. Mais même ainsi, on n’a pas obtenu la réponse optimale.
Puisqu’on suppose, dans cette version “0/1” du problème qu’un objet est soit présent, soit absent (pas de fraction et pas de multiple), on peut représenter l’ensemble des possibilités par un arbre binaire.
Une méthode sûre pour résoudre le problème consiste alors à parcourir l’arbre dans son entièreté et regarder la valeur et le poids de chaque branche complète (de la racine jusqu’à la feuille), pour choisir au final la branche la plus rémunératrice et repectant la contrainte de capacité.
C’est la méthode par force brute.
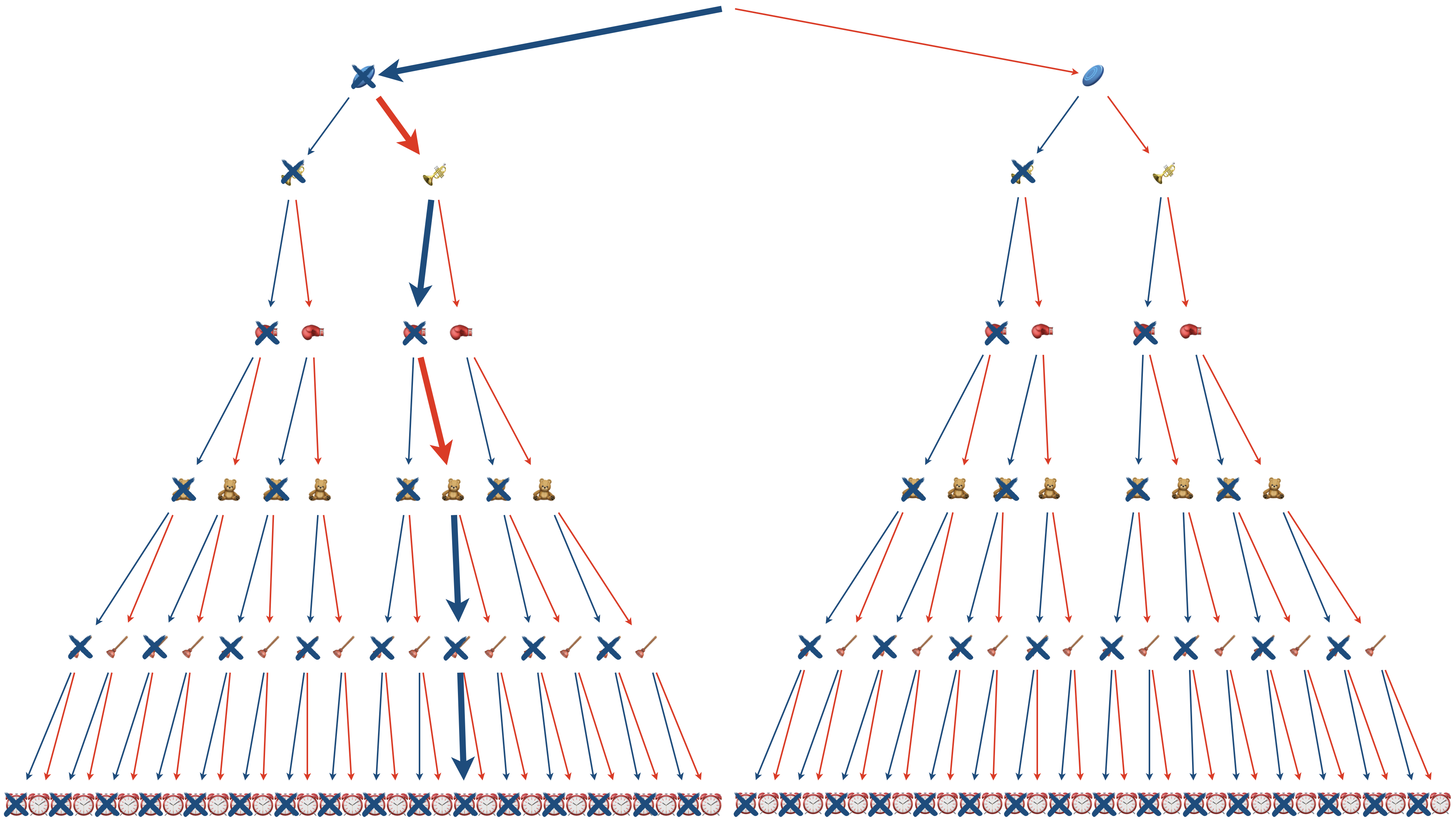
Un algorithme récursif possible pour faire ce travail (à chaque embranchement, on compare avec et sans l’objet) :
def sacadosBrute(v,p,c,i,valeur,poids):
n = len(v)
if i == n:
if poids > c:
return 0
else:
return valeur
else:
valeurAvec = valeur + v[i]
poidsAvec = poids + p[i]
return max(sacadosBrute(v,p,c,i+1,valeur,poids),sacadosBrute(v,p,c,i+1,valeurAvec,poidsAvec))
Comme vous l’aurez deviné, la résolution du problème du sac à dos par force brute est en $O(2^n)$ où $n$ est le nombre d’objets. Donc au-delà de quelques dizaines d’objets, c’est mort…
Pour améliorer les choses, on peut utiliser la méthode “séparation et évaluation” (branch and bond ou BB en anglais) qui vise à élaguer l’arbre autant que faire se peut.
Arrivé à un certain sommet de l’arbre, si l’objet se trouvant en-dessous amène à un dépassement de la capacité, cela ne sert plus à rien de continuer sa branche, alors on coupe.
L’autre idée est d’utiliser la détermination de la valeur optimale du sac par la méthode gloutonne comme une heuristique ; si sous un sommet, la somme des valeurs des objets restant aboutit à une valeur totale inférieure à l’heuristique, on coupe.
Voilà un code possible :
def sacadosBB(v,p,c,i,valeur,poids,meilleure,potentiel):
nbappels += 1
n = len(v)
meilleure = max(meilleure,valeur)
if i == n:
if poids > c:
return 0
else:
return valeur
elif valeur + potentiel[i] < meilleure:
return valeur
else:
valeurAvec = valeur + v[i]
poidsAvec = poids + p[i]
sol = sacadosBB(v,p,c,i+1,valeur,poids,meilleure,potentiel)
if poidsAvec <= c:
sol = max(sol,sacadosBB(v,p,c,i+1,valeurAvec,poidsAvec,meilleure,potentiel))
return sol
Cela donne un arbre bien plus clairsemé sur notre exemple (et avec, qui plus est, une heuristique qui ne nous aide pas des masses, car très mauvaise).
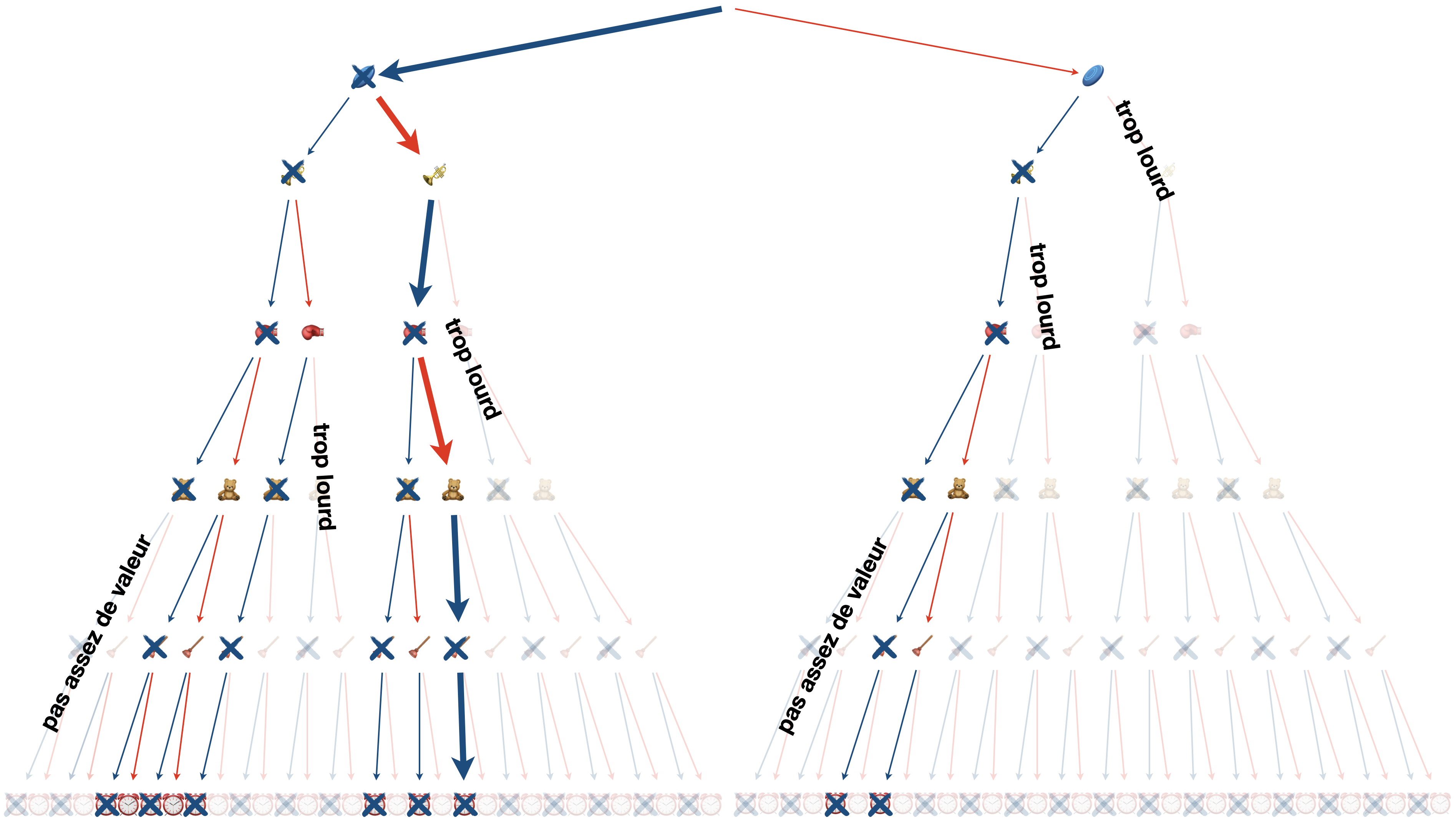
Une autre technique possible est d’utiliser la programmation dynamique qui est présentée dans la vidéo ci-dessous.
La programmation dynamique n’est pas au programme de TSI, mais c’est une part importante du programme des autres sections.
Un chouïa d’apprentissage profond pour les curieux
Géniale série de 4 vidéos de 3Blue1Brown sur les réseaux de neurones :
Chouette récente vidéo de ScienceEtonnante sur les IA génératives :
-
graphe issue de cette introduction assez sympa à l’apprentissage automatique. ↩︎
-
2-ply minimax en anglais ↩︎