Algorithmique numérique
L’informatique n’aime pas les flottants mais les physiciens et les mathématiciens désireux de simulations ou de résolution d’équations font difficilement sans… Il faut alors optimiser les algorithmes pour qu’ils évitent le mieux possible les pièges tendus par le codage fatalement imparfait des nombres réels en machine (pensez à revoir le chapitre en question pour vous rafraîchir la mémoire).
Pivot de Gauss
Deux problèmes liés aux flottants :
- la vérification de la non nullité du pivot
- le choix du pivot
Comment vérifier qu’un pivot potentiel est nul ?
Tester une inégalité entre deux flottants est toujours une mauvaise idée (voirs cours sur la représentation des nombres en machine)
Par exemple, 0.1**2==0.01 renvoie False…
Dans le cas du pivot de Gauss, le plus judicieux est de se donner une tolérance faible adaptée au problème (il faut qu’elle soit suffisamment petite par rapport aux autres valeurs obtenues), et de tester que la valeur absolue du pivot candidat est indérieur à cette valeur.
Par exemple :
tol = 1E-6
if abs(pivot) < tol :
# inspecter le pivot suivant
Comment choisir le plus efficacement le pivot ?
Imaginons que l’on veuille résoudre le système suivant :
$$ \begin{cases} 10^{-4}x &+ &y&=1 \\ \hphantom{10^{-4}}x &+ &y &=2 \\ \end{cases} $$
Et supposons que les calculs se fassent à 3 chiffres significatifs.
En choisissant $\color{red}a_{11}=10^{-4}$ comme pivot, on obtient :
En ne gardant que 3 chiffres significatifs, on se retrouve donc avec le système suivant :
Ce qui donne une solution dans les choux :
$$ \begin{cases} x &= &0 \\ y &= &1 \\ \end{cases} $$
Mais si plutôt que choisir le premier élément comme pivot, nous avions sélectionné le plus grand (en valeur absolu), ce qui correspond ici au choix de $\color{blue}a_{21}=1$ plutôt que $a_{11}=10^{-4}$, nous aurions alors obtenu :
$$ \begin{cases} 0 &x &+&1 &y &=&1 \\ 1 &x &+& 1 &y &=&2 \\ \end{cases} $$
Ce qui donne une nouvelle solution, elle aussi incorrecte, mais quand même beaucoup plus présentable :
$$ \begin{cases} x &= &1 \\ y &= &1 \\ \end{cases} $$
Si le codage des flottants permet plus de 3 chiffres significatifs, il sont malgré tout limités (16 chiffres tout au plus) et cela amène à préférer une stratégie comme la deuxième qui assure un moindre impact des troncatures dues à cette limite.
La méthode du pivot partiel consiste à choisir systématiquement comme pivot le terme de plus grande valeur absolue dans chaque colonne.
Elle permet d’amoindrir les erreurs d’arrondis.
La méthode du pivot total consiste, elle, à chosir comme $i^\text{e}$ pivot le coefficient de valeur absolue maximale dans la matrice $\left(a_{kl}\right)_{k≥i,l≥i}$.
Mais on utilise en pratique très peu cette méthode, car elle nécessite de réordonner les colonnes en plus des lignes (ce qui est lourd).
Interpolation polynomiale de Lagrange
Interpolation : technique consistant à approximer une fonction $f$ à partir seulement d’un ensemble de points ${(x_i,f(x_i))}$.
Interpolation polynomiale de Lagrange : on approxime la fonction par un polynôme devant passer par tous les points.
Le polynôme interpolant $n$ points, s’écrit directement dans la base de Lagrange sous la forme :
$$ P(x) = \sum_{j=1}^n y_j\left(\color{purple}\prod_{i=1,i≠j}^n \frac{x-x_i}{x_j-x_i}\color{black}\right) $$ Par exemple, pour 3 points ${(x_1,y_1),(x_2,y_2),(x_3,y_3)}$, on obtient :
$$ P(x) = y_1\color{purple}\frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}\color{black}+y_2\color{purple}\frac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}\color{black}+y_3\color{purple}\frac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)} $$
L’interpolation polynomiale peut devenir instable dès que le nombre de points augmente, c’est le phénomène de Runge (voir TP).
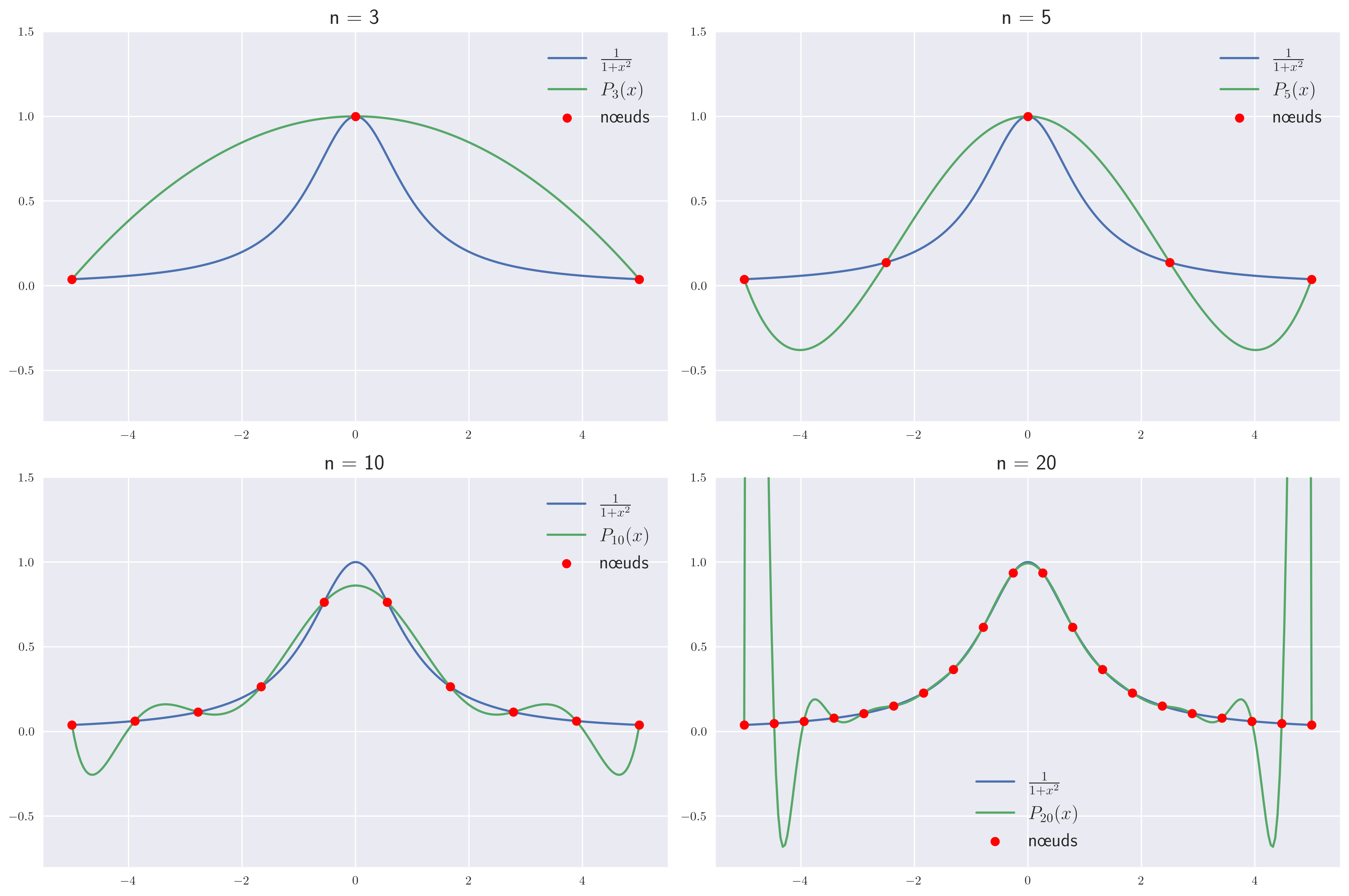
Numériquement, on préfère alors interpoler par morceaux, ce qui permet de se contenter de polynômes de degrés faibles (évitant ainsi les phénomènes d’oscillations).
Interpolation par morceaux
On découpe l’intervalle en morceaux sur lesquels on interpole sur un petit nombre de points.
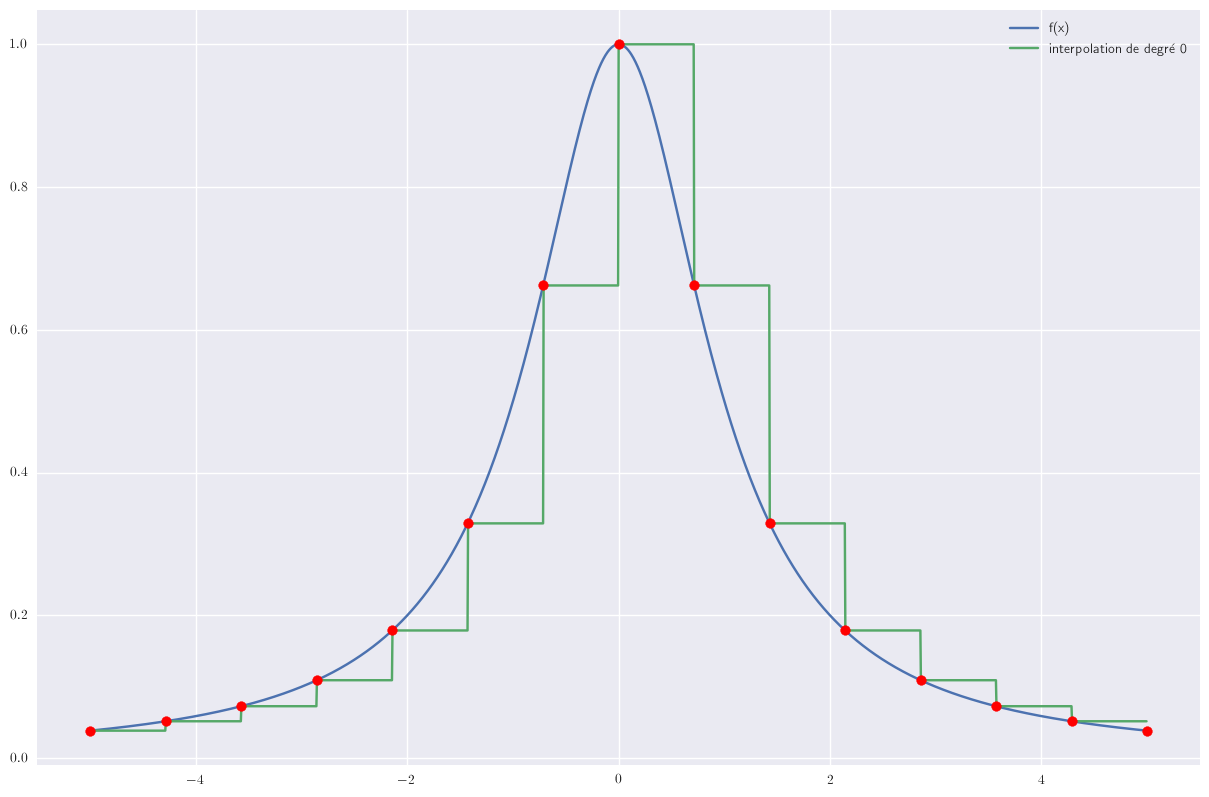
1 point : polynôme de degré 0
Le cas le plus simple correspond à une interpolation de chaque morceau par une constante.
2 points : polynôme de degré 1
Si on garde deux points par morceau, on obtient une interpolation linéaire et l’interpolation globale est une fonction affine par morceau.
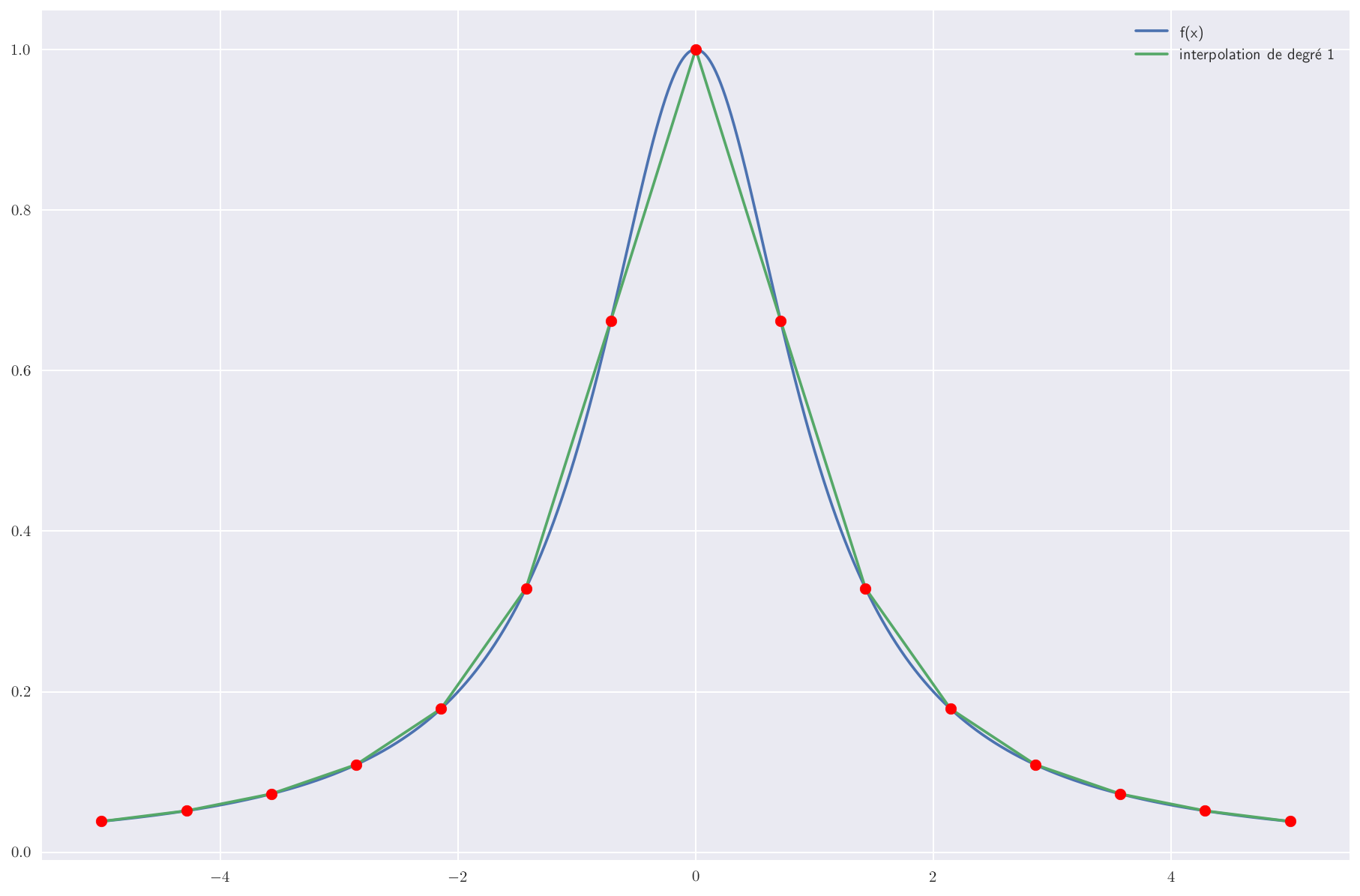
3 points : polynôme de degré 2
Et avec 3 points par morceau, on peut modéliser chaque tronçon par une loi parabolique passant par ces 3 points.
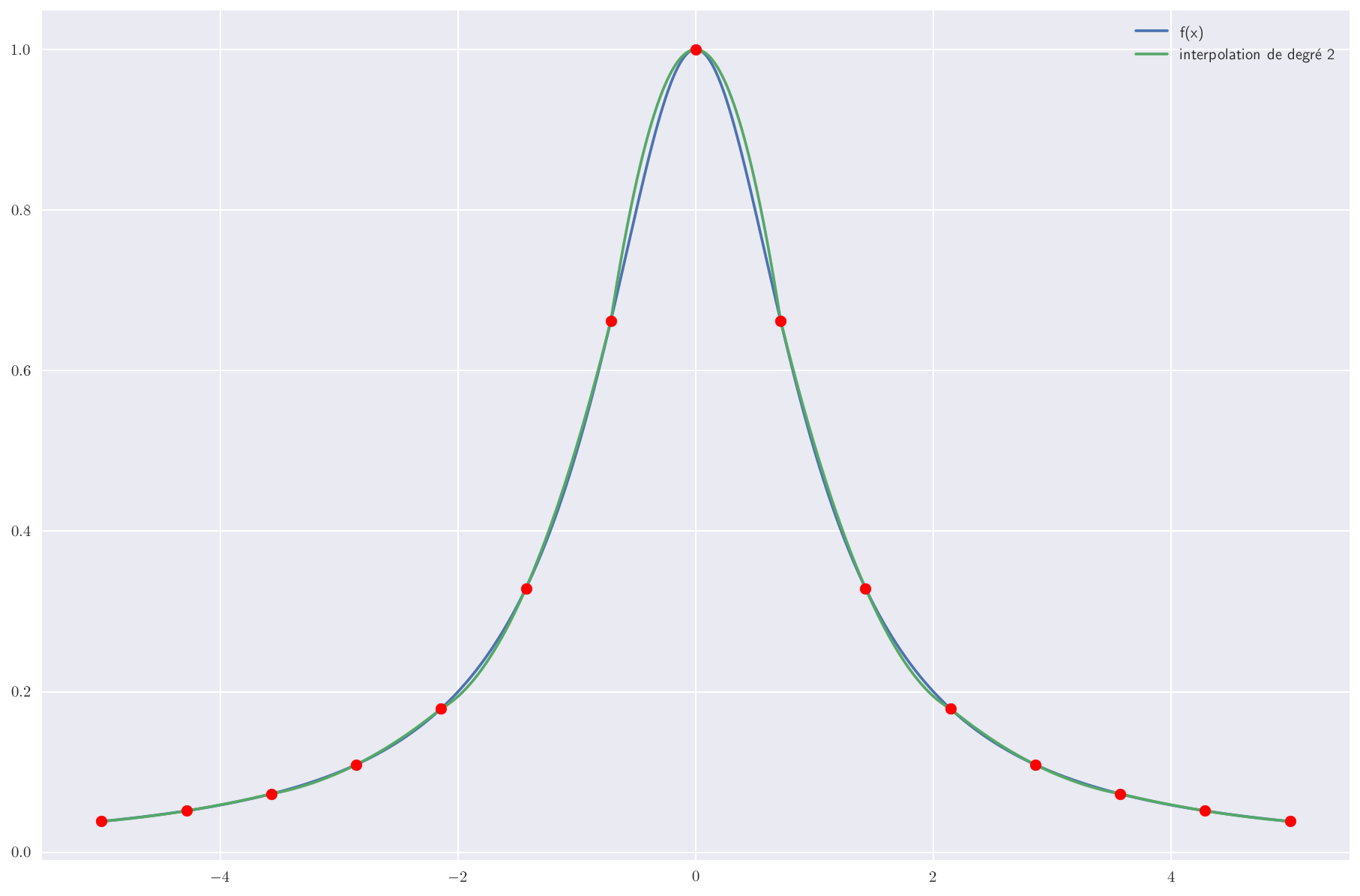
Sur l’exemple de la fonction sinus, l’interpolation par morceau avec des polynômes de degrés 2 donne un très bon résultat.
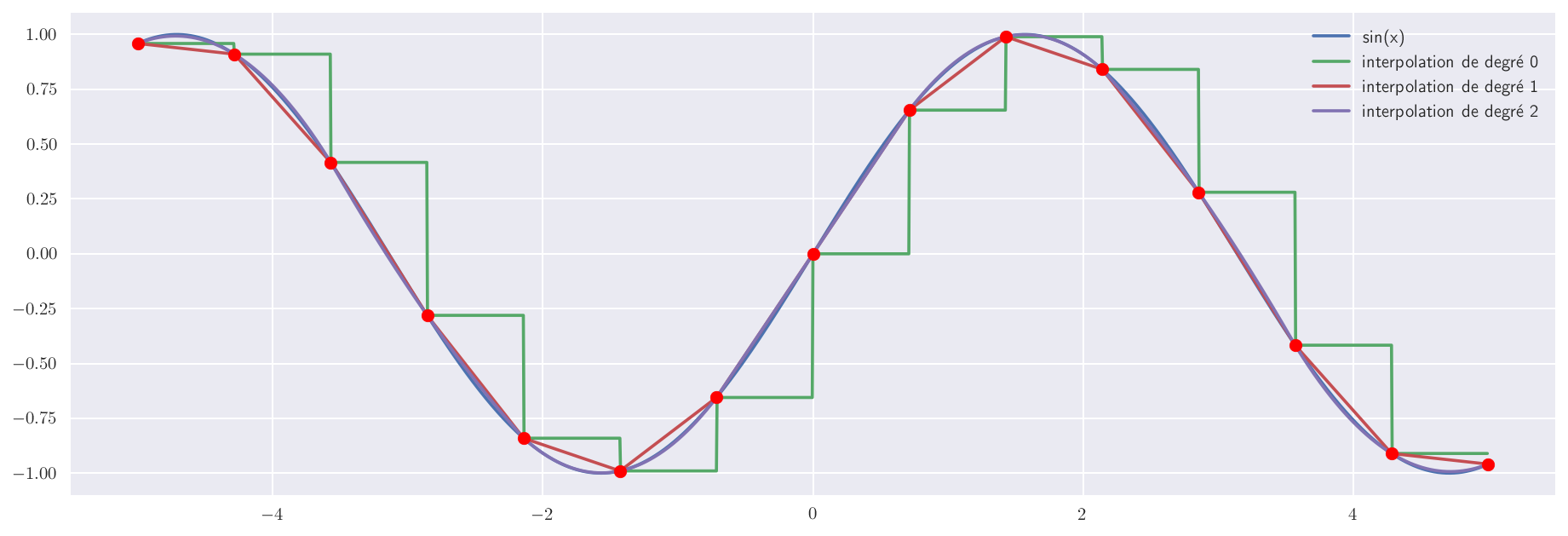
Mais à nouveau, le choix du degré ne doit pas se faire aveuglément comme le montre l’exemple ci-dessous où la fonction discontinue est mal approchée par une interpolation par morceaux de degré 2.
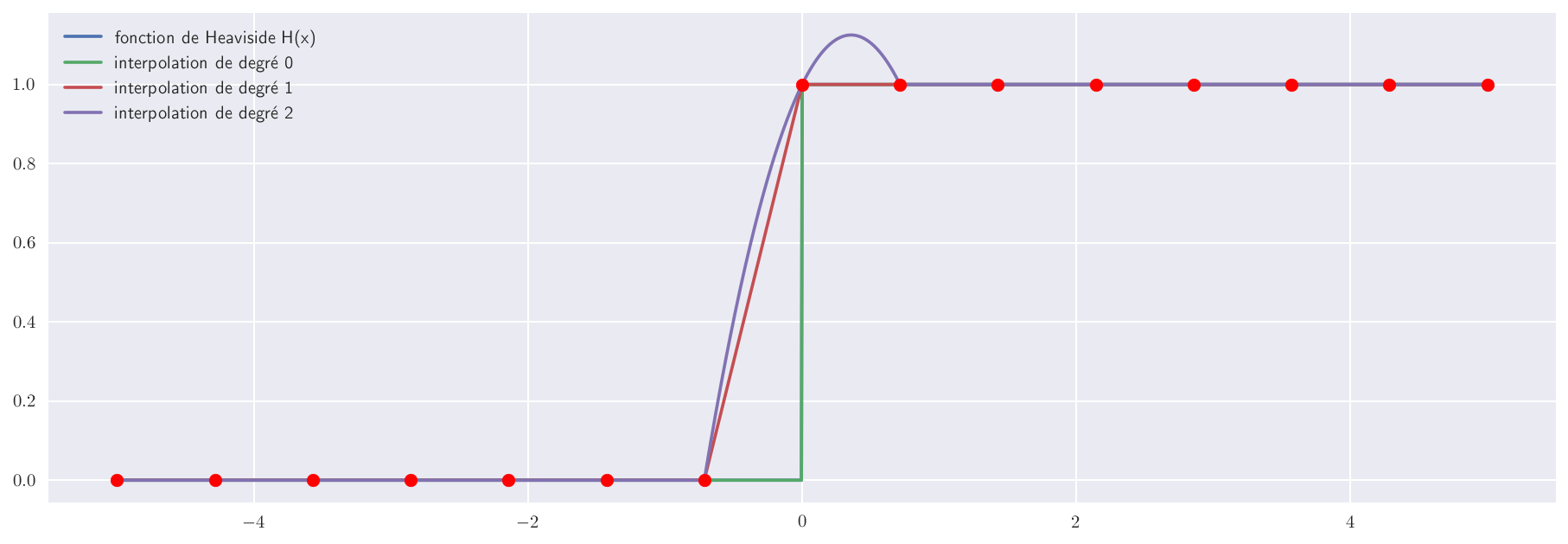
Intégration numérique
L’intégration numérique (ou quadrature) consiste à intégrer (de façon approchée) une fonction sur un intervalle borné $[a, b]$, c’est-à dire calculer l’aire sous la courbe représentant la fonction, à partir d’un calcul ou d’une mesure en un nombre fini $n$ de points.
L’intégration des polynômes étant très simple, l’opération consiste généralement à construire une interpolation polynomiale (de degré plus ou moins élevé) par morceaux (intégration composée) puis d’intégrer le polynôme sur chaque morceau.
On obtient la méthodes des rectangles (à gauche, à droite ou milieu) avec des polynôme de degré 0, la méthode des trapèzes avec des polynômes de degré 1 et la méthode de Simpson avec des polynômes de degré 2 (on va rarement plus loin).
Vous retrouverez un exemple d’implémentation python d’intégration numérique à la fin du TP 2.
Méthode d’Euler
La méthode d’Euler est la technique la plus simple pour déterminer numériquement la solution d’une équation différentielle.
Plus précisément, on cherche la solution au problème de Cauchy suivant :
$$ \begin{cases} y’(t) = f(t,y(t)) \\ y(t_0) = y_0 \\ \end{cases} $$
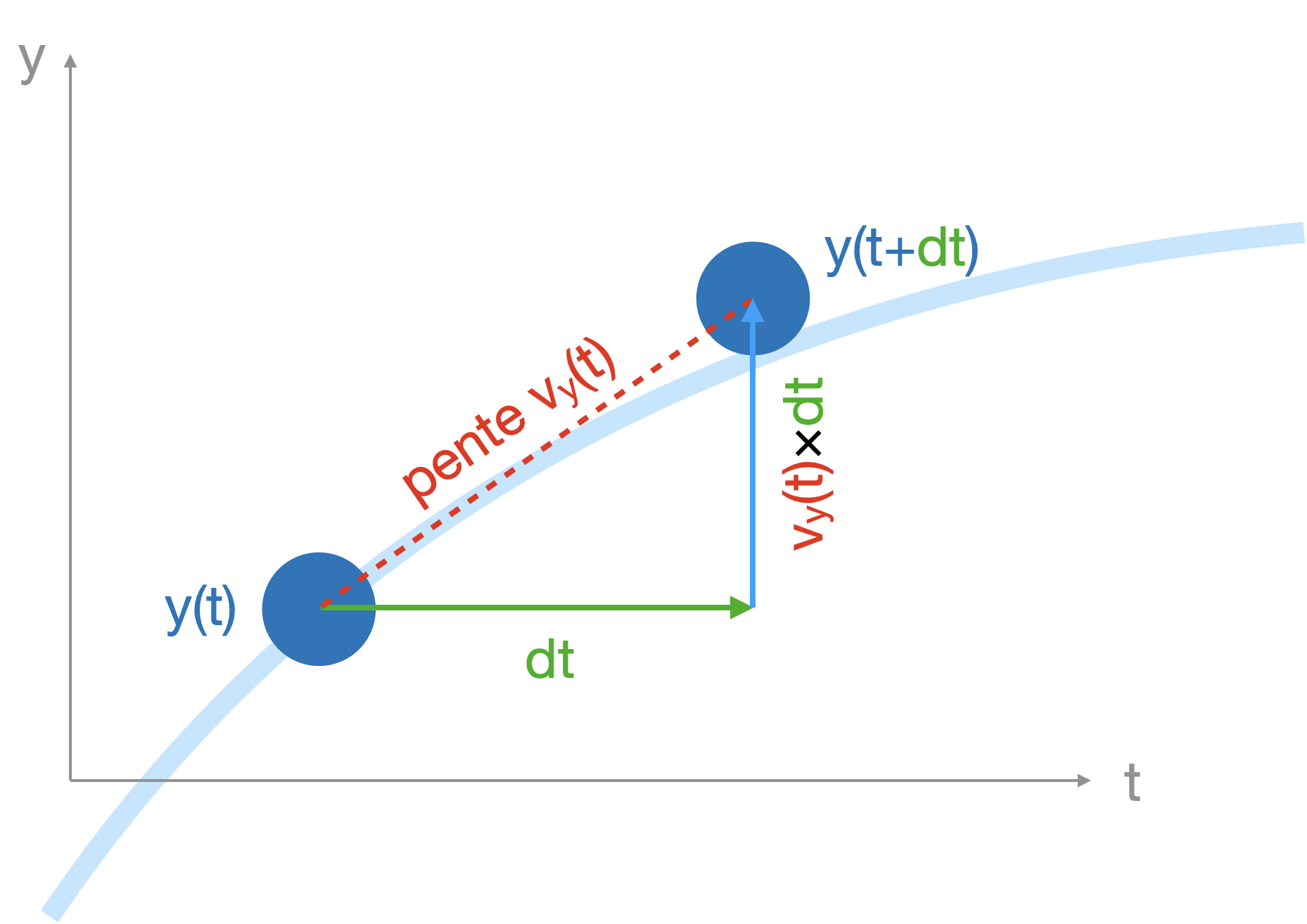
L’idée maîtresse de la méthode est qu’une fonction suffisamment régulière se confond localement avec sa tangente. On va alors découper le temps $t$ et approximer sur chacun des pas la fonction $y(t)$ par sa tangente.
C’est sur la détermination de la pente de la tangente à partir de $f$ que les méthodes de résolution diffèrent.
Méthode d’Euler explicite
- on choisit un pas temporel constant $h$ petit et on pose $t_n=t_0+nh$.
- pour chaque intervalle de temps, entre $t_i$ et $t_{i+1}=t_i+h$, on calcule : $y_{i+1}=y_i + hf(t_i,y_i)$
Illustration avec le mouvement vertical d’un ballon ($h=dt$ et $f(t,y(t))=v_y(t)$) :
Cette méthode ainsi décrite est dite explicite car chaque $y_{i+1}$ est une fonction explicite des $y_j$ pour $j≤i$.
La méthode d’Euler permet d’intégrer des équations différentielles de tout ordre puisqu’une équation diférentielle d’un ordre supérieur à 1 peut toujours s’exprimer comme un système d’équations du premier ordre.
En effet, l’équation $y^{(N)}(t)=f\left(t,y(t),y’(t),\ldots,y^{(N-1)}(t)\right)$ peut se réécrire en introduisant les variables intermédiaires $z_1(t)=y(t),z_2(t)=y’(t),\ldots,z_N(t)=y^{(N-1)}(t)$ :
$$ \pmb{z(t)} = \begin{pmatrix} z’_1(t) \\ \vdots \\ z’_{N-1}(t) \\ z’_N(t) \end{pmatrix}=\begin{pmatrix} y’(t) \\ \vdots \\ y^{(N-1)}(t) \\ y^{(N)}(t) \end{pmatrix} = \begin{pmatrix} z_2(t) \\ \vdots \\ z_N(t) \\ f(t,z_1(t),\ldots,z_N(t)) \end{pmatrix} $$
Il s’agit bien alors d’un système du premier ordre en la variable $\pmb{z(t)}$ et on peut donc utiliser la méthode d’Euler.
Prenons l’exemple de l’équation du mouvement d’un pendule : $$\ddot{\theta}+\frac{g}{L}\sin\theta =0$$ En introduisant $z_1(t)=\theta(t)$ et $z_2(t)=\dot{\theta}(t)$, on se retrouve avec le système d’équations différentielles du premier ordre suivant : $$ \begin{cases} \dot{z_1}(t) = z_2(t) \\ \dot{z_2}(t) = -\frac{g}{L}\sin{z_1(t)} \\ \end{cases} $$
Limites
Erreur de troncature locale
L’erreur de troncature locale de la méthode d’Euler est la petite erreur faite à chaque étape. C’est la différence entre la solution numérique après une étape, $y_1$, et la solution exacte à l’instant $t_1=t_0+h$.
La solution numérique est donnée par : $$y_1 = y_0+hf(t,y_0)$$ Et la solution exacte, donnée par un développement de Taylor autour de $t_0$, s’écrit :
L’erreur vaut la différence : $$y(t_1)-y_1=\frac{1}{2}h^2y’’(t)+O(h^3)$$ Cela montre que pour un petit $h$, l’erreur de troncature locale est approximativement proportionnelle à $h^2$.
Erreur de troncature globale
L’erreur de troncature globale est l’erreur faite à un instant fixe $t$, après tous les pas qu’il a fallu pour arriver à $t$ à partir de $t_0$.
L’erreur de troncature globale correspond ainsi à l’accumulation des erreurs de troncature locale.
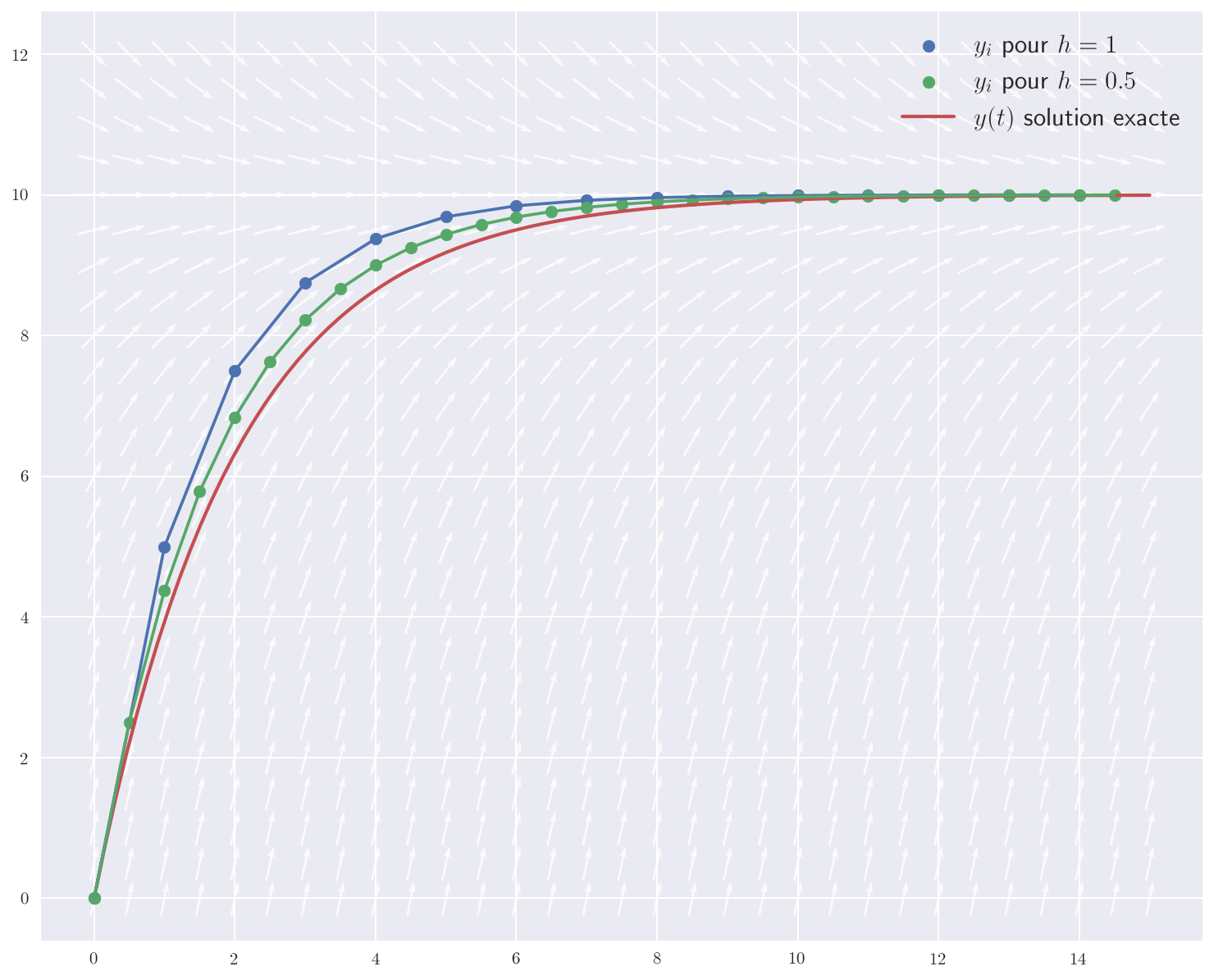
Étant donné que le nombre d’étapes est donné par $\frac{t-t_0}{h}$ ce qui le rend proportionnel à $1/h$ et que l’erreur locale est approximativement proportionnelle à $h^2$, on se retrouve avec une erreur globale proportionnelle à $h$.
Que l’erreur globale soit approximativement linéaire en $h$ est la raison pour laquelle la méthode d’Euler est dite d’ordre 1.
Erreur d’arrondi
On pourrait se dire “qu’à cela ne tienne ! Suffit de prendre un pas rikiki…” Mais un nouveau problème se pose allors : les erreurs d’arrondis.
Du fait des limites du codage des nombres réels en machine, chaque calcul à partir d’un flottant est entâché d’une erreur due à l’arrondi. On exprime généralement cette erreur en fonction de l’epsilon machine $\varepsilon$.
l’epsilon machine ou précision machine est la limite supérieure de l’erreur relative d’approximation causée par l’arrondi.
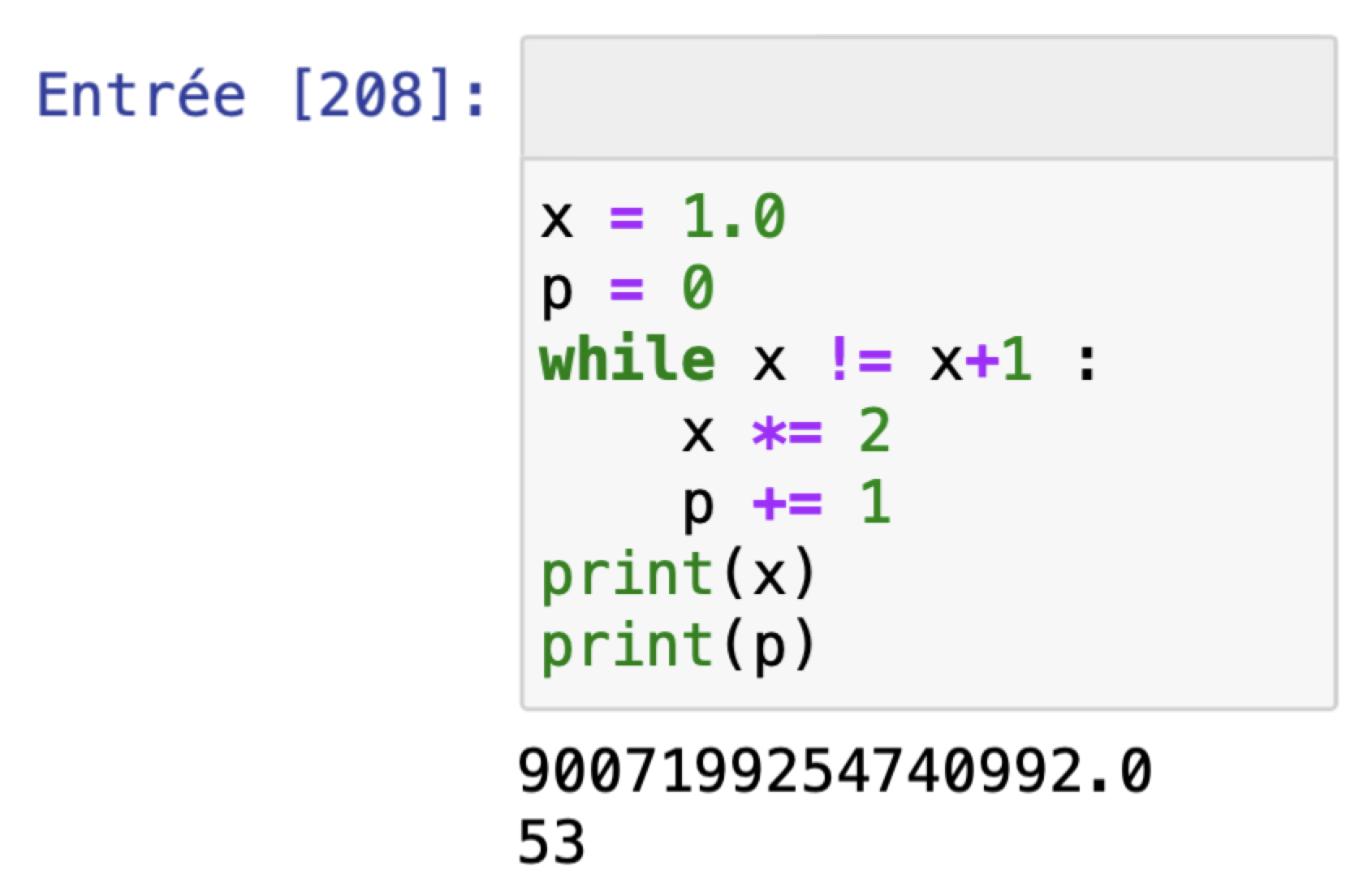
En python, comme la mantisse d’un flottant correspond à 53 bits, l’errreur relative se fait sur le dernier bit et vaut donc $2^{-53}$ ($\varepsilon=2^{-52}$ au pire entre deux arrondis consécutifs).
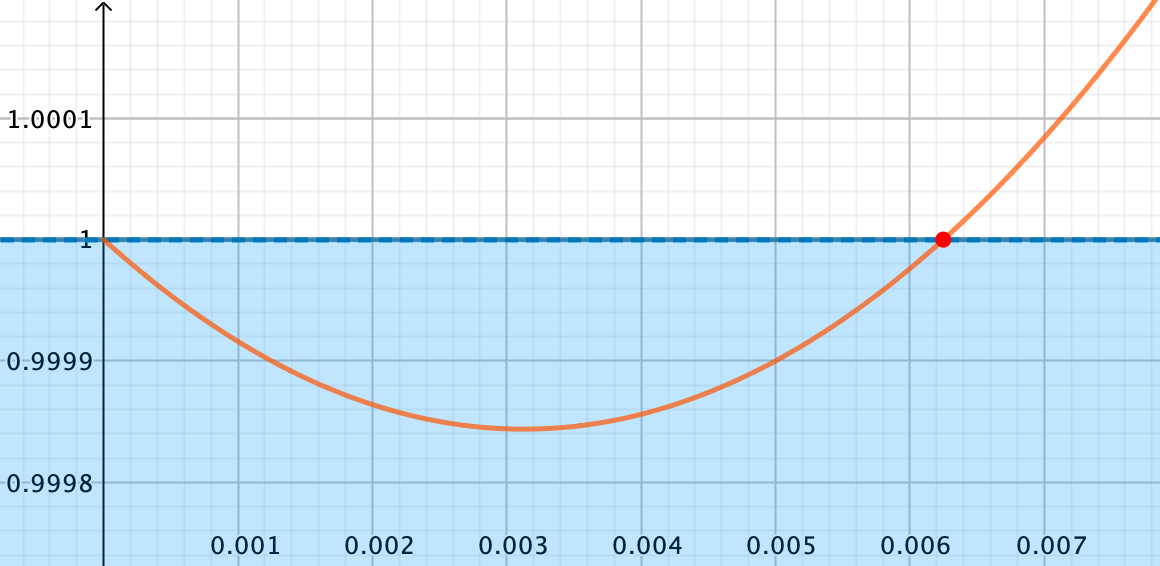
Le code ci-dessous trouve la première puissance de 2, $x$, pour laquelle $x+1$ est arrondie à $x$ (absorption), provoquant une erreur relative (la plus grande possible) de $1/x$.
Par conséquent, l’erreur d’arrondi sur chaque valeur $y_n$ obtenue par la méthode d’Euler est de l’ordre de $\varepsilon y_n$. Et en considérant ces erreurs d’arrondi comme des variables aléatoires indépendantes, l’erreur d’arrondi totale va être de l’ordre de $\varepsilon\sqrt{n}$ où $n$, le nombre de valeurs calculées, est inversement proportionnel au pas.
Finalement, l’erreur d’arrondi globale est proportionnelle à $\frac{\varepsilon}{\sqrt{h}}$ et donc diverge lorsque $h$ tend vers 0 !
Réduire l’erreur de troncature se fait donc au détriment de l’erreur d’arrondi. Néanmoins, on peut se prémunir en bonne part des erreurs d’arrondi grâce à une sommation compensée (algorithme de Kahan).
Stabilité numérique
Comme le montre l’exemple précédent d’un oscillateur harmonique amorti, la méthode d’Euler explicite peut être numériquement instable, la solution numérique s’écartant de plus en plus de la solution exacte.
Si la méthode d’Euler est utilisée sur l’équation linéaire $y’=ky$, alors la solution numérique ne sera stable que si le produit $hk$ est dans la région $\left\{z \in\mathbb{C} ,|1+z| ≤ 1\right\}$.
On obtient en effet : $y_{n+1}=(1+hk)y_n$
Et donc : $y_n = y_0(1+hk)^n$
Le domaine de stabilité correspond à la partie du plan complexe où cette suite géométrique est bornée. Il s’agit bien du disque de centre $z=-1$ et de rayon 1 (en posant $z=hk$).
En généralisant à un système différentiel linéaire de la forme : $y’(t)=My(t)$ (où $M$ est une matrice carrée), il faudra, pour obtenir une solution stable, que chaque valeur propre de $M$ soit dans le disque précédent.
Pour notre exemple, on a : $$\begin{pmatrix}\dot{z}_1\\ \dot{z}_2\end{pmatrix}=\begin{pmatrix}0&1\\ -{\omega_0}^2 & -\frac{\omega_0}{Q}\end{pmatrix}\begin{pmatrix}z_1\\ z_2\end{pmatrix}$$
On obtient deux valeurs propres imaginaires pures si $Q>1/2$ : $$\lambda_{\genfrac{}{}{0pt}{}{1}{2}} = \omega_0\left(\frac{1}{2Q} \pm i\sqrt{\left(1-\frac{1}{2Q}\right)^2}\right)$$ et donc pour que $hk=h\lambda_{\genfrac{}{}{0pt}{}{1}{2}}$ soit à l’intérieur du domaîne de stabilité, il faut que $\left(-\frac{h\omega_0}{2Q}+1\right)^2 + \left(\frac{h\omega_0}{2Q}\right)^2(4Q^2-1) ≤ 1$.
En passant la valeur de $h$ à
0.002dans le programme de l’oscillateur harmonique amorti, on constate effectivement que l’amplitude de l’oscillation daigne bien maintenant diminuer…
Pour résumer, la méthode d’Euler explicite a pour qualité d’être très simple à coder, mais elle cumule de nombreux défauts…
Méthode d’Euler implicite
Si plutôt qu’évaluer $f$ au point de départ ($t_n$,$y_n$), on l’évalue au point d’arrivée ($t_{n+1}$,$y_{n+1}$), on obtient la méthode d’Euler implicite :
$$y_{n+1}=y_n+hf(t_{n+1},y_{n+1})$$
La méthode est dite implicite car $y_{n+1}$ est présent dans les deux membres. Par conséquent, on doit à chaque étape résoudre une équation pour déterminer le nouveau point, ce qui rend l’implémentation plus coûteuse.
Cette méthode est aussi d’ordre 1, mais son domaîne de stabilité est beaucoup plus grand que celui de la méthode explicite puisqu’il s’agit de l’extérieur du disque de rayon 1 centré sur (1;0). Cela permet de l’utiliser sur les équations différentielles raides.
Les méthodes explicites et implicites présentent toutes deux un gros défaut pour qui s’attelle à la résolution de problèmes de mécanique : elles ne conservent pas l’énergie !
La méthode explicite va avoir tendance à ajouter de l’énergie dans le système alors que la métode implicite va avoir tendance à en enlever (ce qu’on peut mettre en lien avec sa plus grande stabilité).
L’idée pour conserver l’énergie est alors d’utiliser une combinaison des deux méthodes.
Méthode d’Euler semi-implicite
C’est la méthode la plus pratique pour résoudre des problèmes de mécanique. Elle allie la simplicité de la méthode explicite (elle est même plus simple à implémenter !) et le stabilité de la méthode implicite. Et surtout, elle conserve l’énergie.
Pour un système du deuxième ordre, on va écrire :
$$\begin{cases}z_2(t_{n+1}) = z_2(t_n) + h f(t_n,z_1(t_n),z_2(t_n)) \\ z_1(t_{n+1}) = z_1(t_n) + h z_2(t_{n+1}) \end{cases}$$
On utilise donc la valeur de $z_2(t_{n+1})$ qui vient d’être mise à jour dans le calcul de $z_1(t_{n+1})$.
Dans le cas de la détermination de la position d’un mobile à partir d’une équation différentielle du 2e ordre, on détermine donc d’abord la nouvelle vitesse, puis la position à partir de cette nouvelle vitesse.
La méthode est là encore d’ordre 1. On constate que si l’amplitude est maintenant proprement modélisée, c’est au détriment d’un déphasage entre la solution numérique et la solution exacte d’autant plus important que la pas est grand.
Méthodes d’ordre supérieur
La méthode Runge Kutta d’ordre 2 (ou méthode de Heun, ou méthode d’Euler améliorée) consiste à moyenner la valeur de la pente de la tangente au point $(t_i,y_i)$ et au point $(t_{i+1},y_{i+1})$, mais comme on ne connaît pas encore $y_{i+1}$, on utilise comme approximation la valeur donnée par la méthode d’Euler explicite :
$$\begin{cases} k_1 = f(t_i,y_i)\\ k_2 = f(t_{i+1},y_i+hk_1) \\ y_{k+1} = y_k + h\frac{k_1+k_2}{2}\end{cases}$$
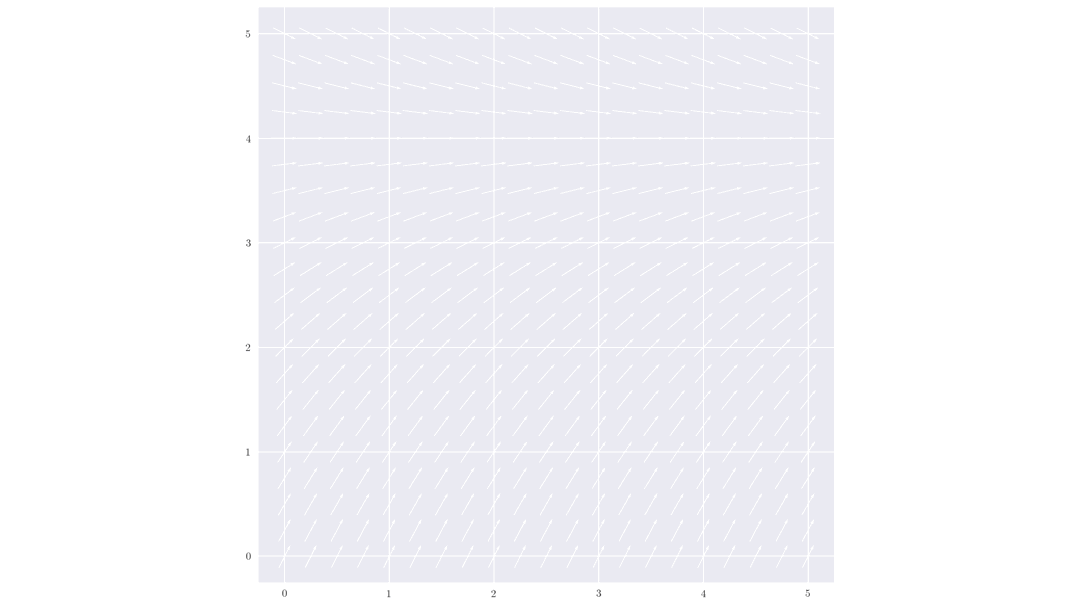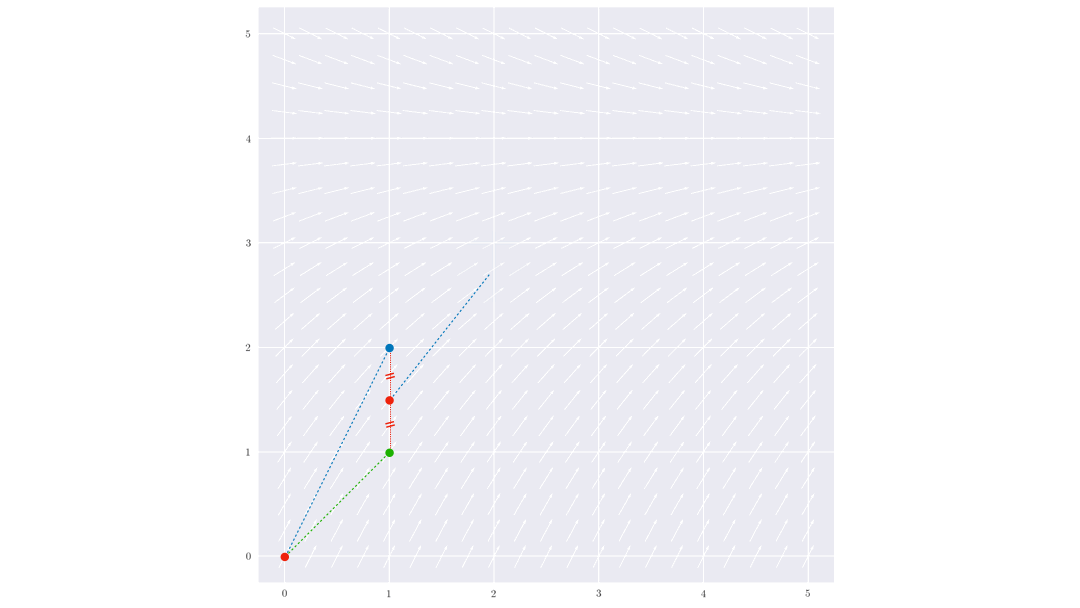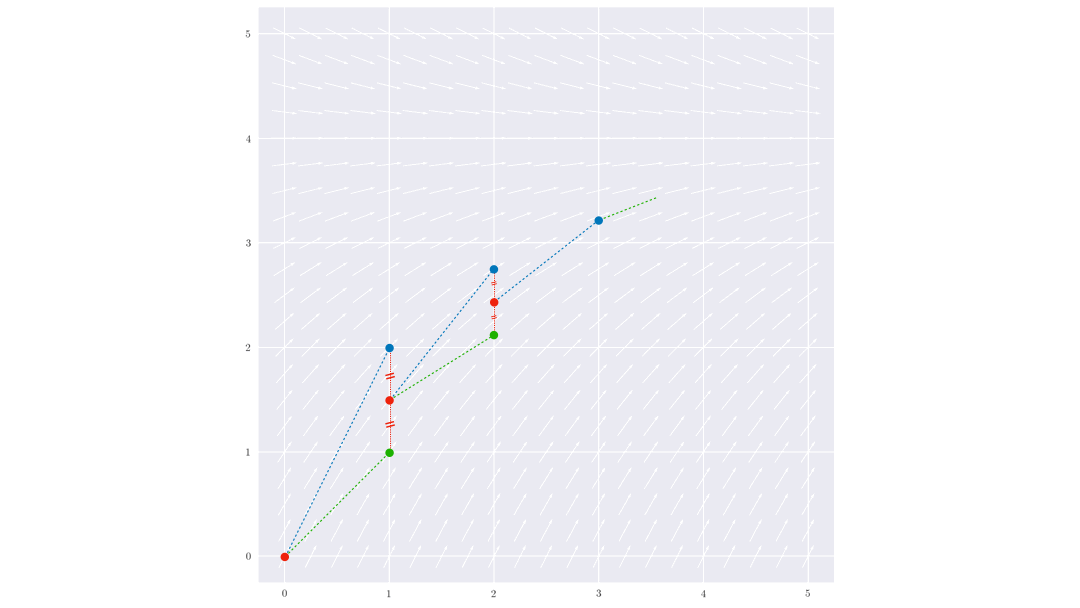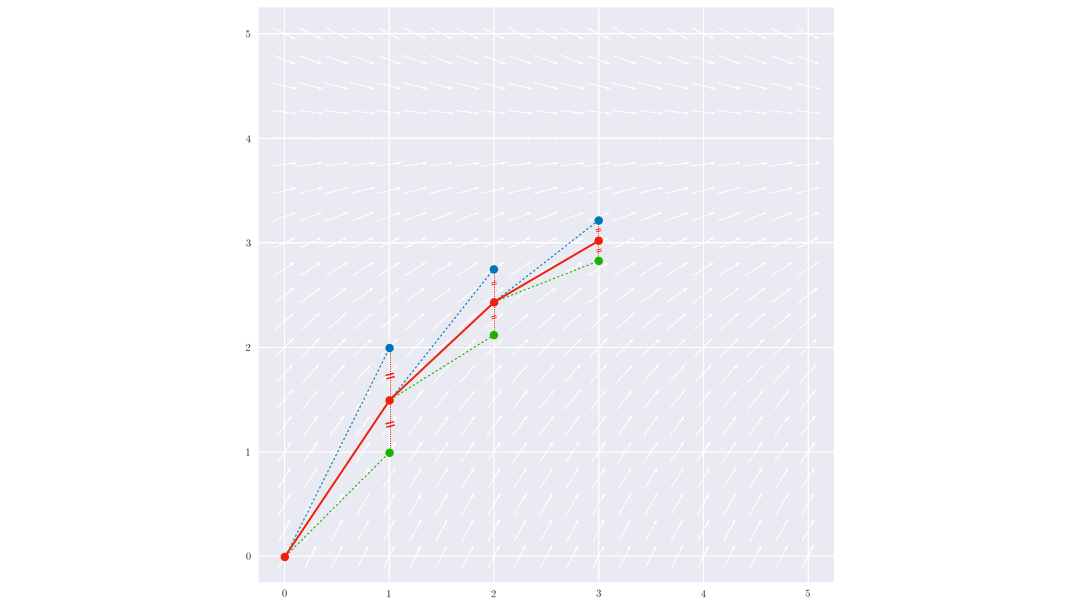
On obtient ainsi une méthode d’ordre 2 (l’erreur de troncature globale est proportionnelle à $h^2$).
On peut aller encore plus loin en introduisant un point au milieu de l’intervalle et en moyennant 4 pentes de tangente différentes :
- la pente $k_1$ au début de l’intervalle, déjà connue,
- la pente $k_2$ au milieu de l’intervalle que l’on approxime en utilisant une première estimation de $y_{i+1/2}$ grâce à $k_1$,
- la pente $k_3$ au milieu de l’intervalle que l’on approxime en utilisant une seconde estimation de $y_{i+1/2}$ grâce à $k_2$,
- la pente $k_4$ à la fin de l’intervalle que l’on approxime en utilisant une estimation de $y_{i+1}$ grâce à $k_3$.
$$\begin{cases} k_1 = f(t_i,y_i)\\ k_2 = f(t_{i+1/2},y_i+h\frac{k_1}{2}) \\ k_3 = f(t_{i+1/2},y_i+h\frac{k_2}{2}) \\ k_4 = f(t_{i+1},y_i+hk_3) \\ y_{k+1} = y_k + h\frac{k_1+2k_2+2k_3+k_4}{6}\end{cases}$$
On obtient alors la méthode Runge Kutta d’ordre 4 (RK4) qui, comme son nom l’indique, est d’ordre 4. C’est sans doute la méthode la plus utilisée car elle donne des résultats précis et fidèles pour des pas n’ayant pas besoin d’être trop petits.
On peut écrire que :
$y(t_{n+1}) = y(t_n)+\int_{t_n}^{t_{n+1}}f(t,y(t))dt$
Résoudre numériquement l’équation différentielle revient donc à intégrer la fonction $f$ sur chaque pas. Et si pour cela on applique les méthodes de quadratures évoquées plus haut (et au TP2) on retrouve que :
● la méthode des rectangles à gauche correspond à la méthode d’Euler explicite ;
● la méthode des rectangles à droite correspond à la méthode d’Euler implicite ;
● la méthode des trapèzes correspond à la méthode Runge Kutta d’ordre 2 ;
● la méthode de Simpson correspond à la méthode Runge Kutta d’ordre 4.