TP 11 : algorithmique numérique

Cliquez sur cette invitation pour récupérer le repository du TP.

Pivot de Gauss

On cherche résoudre un système d’équations grâce à la méthode du pivot de Gauss (on ne considèrera que des systèmes de n équations avec un nombre d’inconnues inférieur ou égal à n).

Pour cela, on crée une fonction qui transforme la matrice augmentée obtenue à partir du sytème en une matrice échelonnée.

def Gauss(M,recherchePivot):
    """
    préconditions: M une liste de listes (matrice) contenant des nombres.
                   recherchePivot est une fonction ayant pour paramètres la matrice et deux indices 
                   et renvoyant l'indice du prochain pivot.
    postcondition: M est mutée sous la forme d'une matrice échelonnée.
    La fonction ne retourne rien (elle a juste un effet de bord).
    """
    m = len(M)                                   # nombre de lignes de la matrice M
    n = len(M[0])                                # nombre de colonnes
    h = k = 0
    tol = 1e-9                        
    while h < m and k < n:                       # h sera l'indice des lignes et k celui des colonnes
        ipivot = recherchePivot(M,h,k)           # à déterminer par la suite
        pivot = M[ipivot][k]
        if abs(pivot) < tol:                     # pour tester la nullité d'un candidat pivot
            k += 1
        else:
            if h != ipivot:
                M[h],M[ipivot] = M[ipivot],M[h]  # on permute la ligne du pivot et celle correspondant à h
            for j in range(k,n):
                M[h][j] /= pivot                 # on normalise la ligne du pivot pour avoir 1 dans la diagonale
            for i in range(h+1,m):
                f = M[i][k]
                for j in range(k,n):
                    M[i][j] -= M[h][j] * f       # Li <- Li - Lh
            h +=1
            k += 1

Il ne reste plus qu’à définir la fonction recherchePivot…
Dans sa version naïve, il s’agit simplement du prochain élément dans la diagonale.

Écrire la fonction recherchePivotNaive correspondante en essayant de vous y retrouver avec les indices. La fonction doit retourner l’indice du pivot.

def recherchePivotNaive(M: list,h: int,k: int) -> int:
    # VOTRE CODE

Correction (cliquer pour afficher)

def recherchePivotNaive(M,h,k):
    return h

Tout simplement...

On va utiliser un module permettant d’avoir la main sur le codage machine des flottants : decimal.
Les valeurs de la matrice que l’on va construire ci-dessous seront limitées à 4 chiffres significatifs et l’arrondi se fera à la valeur inférieure (pour reproduire la troncature imposée par le codage des nombres).

import decimal
from decimal import Decimal
decimal.getcontext().prec= 4
decimal.getcontext().rounding = decimal.ROUND_DOWN

A = [[Decimal(20),Decimal(15),Decimal(10),Decimal(45)],
     [Decimal(-3),Decimal(-2.249),Decimal(7),Decimal(1.751)],
     [Decimal(5),Decimal(1),Decimal(3),Decimal(9)]]

for ligne in A:
    print(ligne)

[Decimal('20'), Decimal('15'), Decimal('10'), Decimal('45')]
[Decimal('-3'), Decimal('-2.249000000000000110134124042815528810024261474609375'), Decimal('7'), Decimal('1.750999999999999889865875957184471189975738525390625')]
[Decimal('5'), Decimal('1'), Decimal('3'), Decimal('9')]

Pour que l’affichage soit plus propre, on reconvertit les flottants “Decimal” en flottants python habituels.

def affiche(M):
    for l in M:
        for e in l:
            print(f"{float(e):^10}",end="")
        print()
affiche(A)

20.0      15.0      10.0      45.0   
-3.0     -2.249     7.0      1.751   
5.0       1.0       3.0       9.0

Appliquons la méthode du pivot de Gauss avec recherche naïve du pivot sur la matrice A :

Gauss(A,recherchePivotNaive)
affiche(A)

1.0       0.75      0.5       2.25   
0.0       1.0      8500.0    8500.0  
0.0       0.0       1.0      0.9995

Construisons maintenant une fonction substitution qui part d’une matrice échelonnée $M_{n,n+1}$ et qui en déduit le vecteur solution $V$ du système d’équations représenté par la matrice.

$\color{green}V \color{black} = (\color{green}v_1\color{black},\color{green}v_2\color{black},\color{green}\ldots\color{black},\color{green}v_n\color{black})^t$ est tel que :

$$ \begin{cases} m_{11}\,\color{green}v_1\color{black} +m_{12}\,\color{green}v_2\color{black} + \ldots + m_{1n}\,\color{green}v_n\color{black} = m_{1\,n+1} \\m_{21}\,\color{green}v_1\color{black}+m_{22}\,\color{green}v_2\color{black} + \ldots + m_{2n}\,\color{green}v_n\color{black} = m_{2\,n+1} \\ \quad\vdots \qquad\qquad\vdots\;\;\;\;\;\;\;\;\ddots\qquad \vdots \qquad\qquad\vdots\\m_{n1}\,\color{green}v_1\color{black} +m_{n2}\,\color{green}v_2\color{black} + \ldots + m_{nn}\,\color{green}v_n\color{black} = m_{n\,n+1} \end{cases} $$

où $m_{ii} = 1$ pour $i$ allant de $1$ à $n$, et où $m_{i,j}=0$ pour $i>j$.

def substitution(M):
    """
    précondition: M est une matrice (liste de listes) échelonnée de dimension n*(n+1)
    postcondition: la fonction retourne le vecteur solution V
    """
    n = len(M)
    V = [0]*n
    # VOTRE CODE
    return V

Correction (cliquer pour afficher)

def substitution(M):
    n = len(M)
    V = [0]*n
    for i in range(n-1,-1,-1):
        V[i] = M[i][n]
        for j in range(i+1,n):
            V[i] -= M[i][j]*V[j]
        V[i] /= M[i][i]
    return V

def afficheSolution(M):
    """
    v est le vecteur solution
    """
    sol  = ['x','y','z']
    v = substitution(M)
    for xi,vi in zip(sol,v):
        print(xi,"=",vi)
afficheSolution(A)

x = -1.999
y = 5
z = 0.9995

Reprenons la fonction recherchePivot afin d’implémenter la méthode du pivot partiel.
Pour cela, recherchePivotPartiel devra fournir l’indice de la ligne où se trouve l’élément de plus grande valeur absolue parmi les éléments sur la diagonale et en dessous (≥h) dans la colonne considérée (k).

def recherchePivotPartiel(M: list,h: int,k: int) -> int:
    # VOTRE CODE

Correction (cliquer pour afficher)

def recherchePivotPartiel(M,h,k):
    ipivot, pivot = h, abs(M[h][k])
    for i in range(h+1,len(M)):
        if abs(M[i][k]) > pivot:
            pivot = abs(M[i][k])
            ipivot = i
    return ipivot

A = [[Decimal(20),Decimal(15),Decimal(10),Decimal(45)],
     [Decimal(-3),Decimal(-2.249),Decimal(7),Decimal(1.751)],
     [Decimal(5),Decimal(1),Decimal(3),Decimal(9)]]

print("Matrice de départ :")
affiche(A)

print("\nForme échelonnée avec méthode du pivot partiel :")
Gauss(A,recherchePivotPartiel)
affiche(A)

print("\nSolution :")
afficheSolution(A)

Matrice de départ :
20.0      15.0      10.0      45.0   
-3.0     -2.249     7.0      1.751   
5.0       1.0       3.0       9.0    
    
Forme échelonnée avec méthode du pivot partiel :
1.0       0.75      0.5       2.25   
0.0       1.0     -0.1818    0.8181  
0.0       0.0       1.0      0.9998  
    
Solution :
x = 1.000
y = 0.9998
z = 0.9998

On constate que la méthode avec pivot partiel est beaucoup moins aux fraises que la méthode naïve…

Quelle est la complexité de la méthode du pivot de Gauss ainsi construite ?
a : linéaire
b : quadratique
c : cubique
d : polynomiale de degré > 3

Correction (cliquer pour afficher)

Cubique.
Le nombre de calculs à chaque itération correspond au nombre de cases bleues dans l'image ci-dessous. Il s'agit en effet à chaque fois de créer une nouvelle colonne de zéro sous le pivot par combinaisons linéaires avec la ligne du pivot.
On se retrouve finalement avec une somme de carrés consécutifs en terme de nombre d'opérations, ce qui donne un polynôme de degré 3 en la taille de la matrice.

Interpolation polynomiale de Lagrange

Présentation

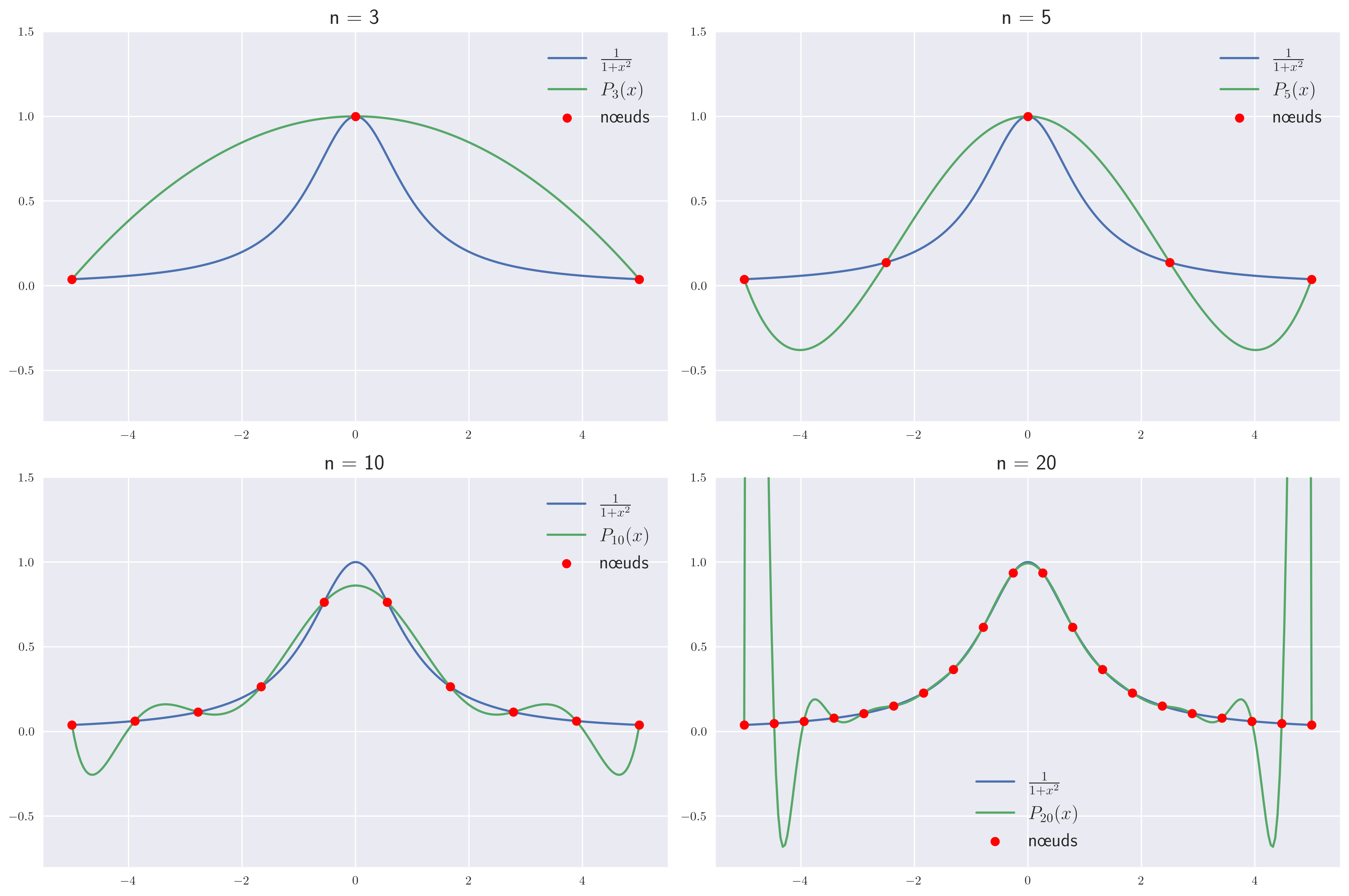
Phénomène de Runge

L’augmentation du nombre $n$ de points d’interpolation ne constitue pas nécessairement une bonne stratégie d’approximation comme on va le voir dans l’exemple suivant.

Définir en Python dans la cellule ci-dessous la fonction $f:x\mapsto\frac{1}{1+x^2}$.
La fonction devra s’appeler f.

Correction (cliquer pour afficher)

def f(x):
    return 1/(1+x**2)

Construisez maintenant le polynôme d’interpolation de Lagrange en suivant la formule du cours.
Attention : le nombre de points $n$ est un paramètre de la fonction construite.

def interp(f, n: int, interv: tuple, x: float) -> float:
    """
    postcondition: la fonction retourne P(x) où P est le polynôme d'interpolation de Lagrange de f passant par les n points.
    """
    debut,fin = interv[0],interv[1]
    X = [debut + i*(fin-debut)/(n-1) for i in range(n)]
    Y = [f(x) for x in X]
    # VOTRE CODE
    return s

Correction (cliquer pour afficher)

def interp(f,n,interv,x):
    debut,fin = interv[0],interv[1]
    X = [debut + i*(fin-debut)/(n-1) for i in range(n)]
    Y = [f(x) for x in X]
    s = 0
    for i in range(n):
        p = 1
        for j in range(n):
            if j != i:
                p *= (x-X[j])/(X[i]-X[j])
        s += Y[i]*p
    return s
C'est la traduction Python de la formule mathématique)
$\displaystyle P(x) = \sum_{j=1}^n y_j\left(\color{purple}\prod_{i=1,i≠j}^n \frac{x-x_i}{x_j-x_i}\color{black}\right)$
La somme est dans la boucle extérieure et le produit dans la boucle intérieure.

Quelle est la complexité de la fonction interp en fonction du nombre de nœuds $n$ ?

a : linéaire
b : quadratique
c : cubique

Correction (cliquer pour afficher)

Quadratique

On est paré pour illustrer le phénomène de Runge :

import matplotlib.pyplot as plt
plt.style.use('seaborn')
params = {'figure.figsize': (15, 10),
          'axes.titlesize': 'xx-large',
          'text.usetex':True,
          'figure.dpi': 150}
plt.rcParams.update(params)
fig, axs = plt.subplots(2, 2)

I = 250
intervalle = (-5,5)
X = [intervalle[0] + (intervalle[1]-intervalle[0])*i/I for i in range(I+1)]
Y = [f(x) for x in X]
k = 0
for n in [3,5,10,20]:
    axs[k//2,k%2].set_xlim([-5.5,5.5])
    axs[k//2,k%2].set_ylim([-0.8,1.5])
    # plot de f(x)
    axs[k//2,k%2].plot(X,Y,label=r"$\frac{1}{1+x^2}$")
    # plot de P_n(x)
    Xn,Yn = [],[]
    for x in X:
        Xn.append(x)
        Yn.append(interp(f,n,intervalle,x))
    axs[k//2,k%2].plot(Xn,Yn,label=r"$P_{{{}}}(x)$".format(n))
    axs[k//2,k%2].set_title(f"n = {n}")
    # Plot des noeuds
    Noeuds = [intervalle[0] + (intervalle[1]-intervalle[0])*i/(n-1) for i in range(n)]
    P_noeuds = [interp(f,n,intervalle,noeud) for noeud in Noeuds] 
    axs[k//2,k%2].scatter(Noeuds,P_noeuds,c="r",zorder=10,label="nœuds")
    axs[k//2,k%2].legend(fontsize = 15)
    k += 1
plt.tight_layout()

Interpolation par morceaux

On découpe maintenant l’intervalle d’étude en $N-1$ sous-intervalles (découpés par $N$ nœuds) et on interpole la fonction sur un petit nombre de points sur chacun de ces intervalles.

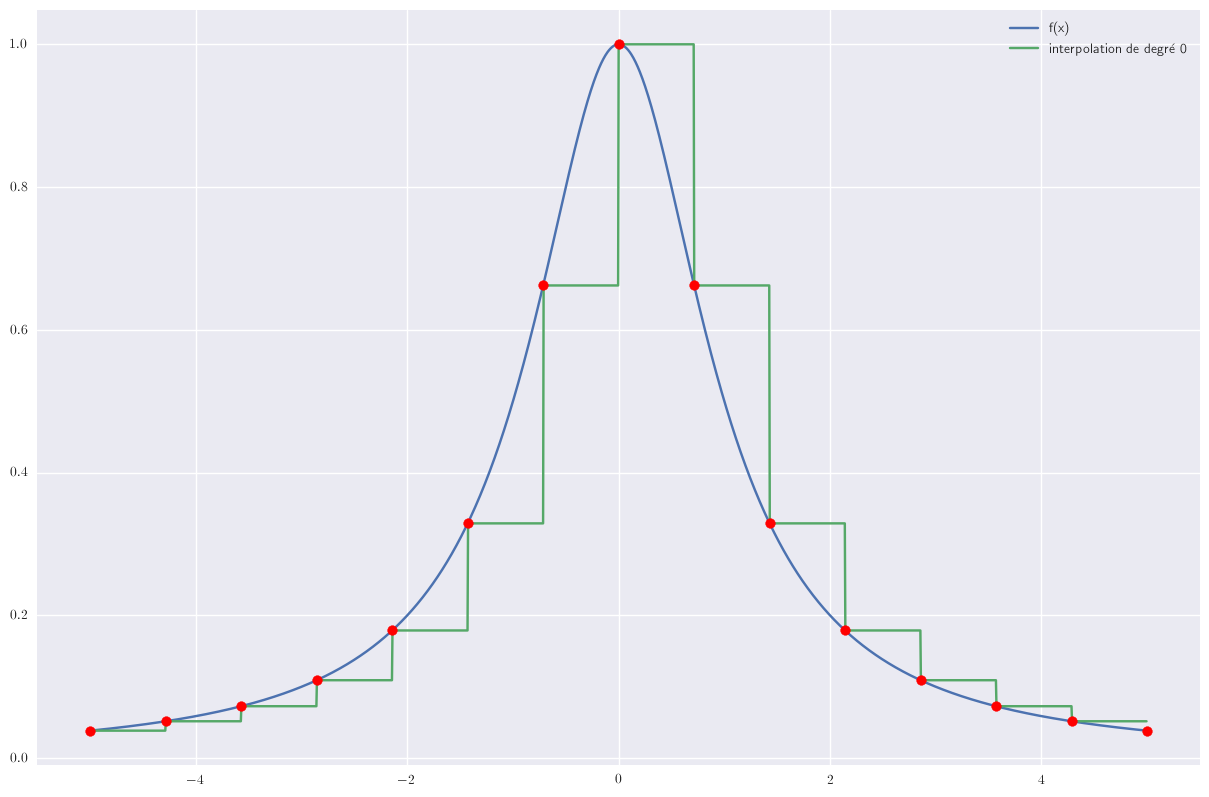
Degré 0

La fonction suivante produit une interpolation par morceaux de degré 0 de la fonction f.
N est le nombre de nœuds.

def interp_rect(f,interv,N,x):
    debut,fin = interv[0],interv[1]
    X = [debut + i*(fin-debut)/(N-1) for i in range(N)]
    for i in range(N-1):
        if X[i] <= x < X[i+1]:
            return f(X[i])

nb = 2000 # nb de points pour le tracé
N = 15
intervalle = (-5,5)
X = [intervalle[0] + (intervalle[1]-intervalle[0])*i/nb for i in range(nb)]
Y1 = [f(x) for x in X]
Y2 = [interp_rect(f,intervalle,N,x) for x in X]
plt.plot(X,Y1,label = "f(x)")
plt.plot(X,Y2,label = "interpolation de degré 0")
Noeuds = [intervalle[0] + (intervalle[1]-intervalle[0])*i/(N-1) for i in range(N-1)]
f_noeuds = [f(n) for n in Noeuds]
plt.scatter(Noeuds,f_noeuds,c='r',zorder=3)
plt.legend()

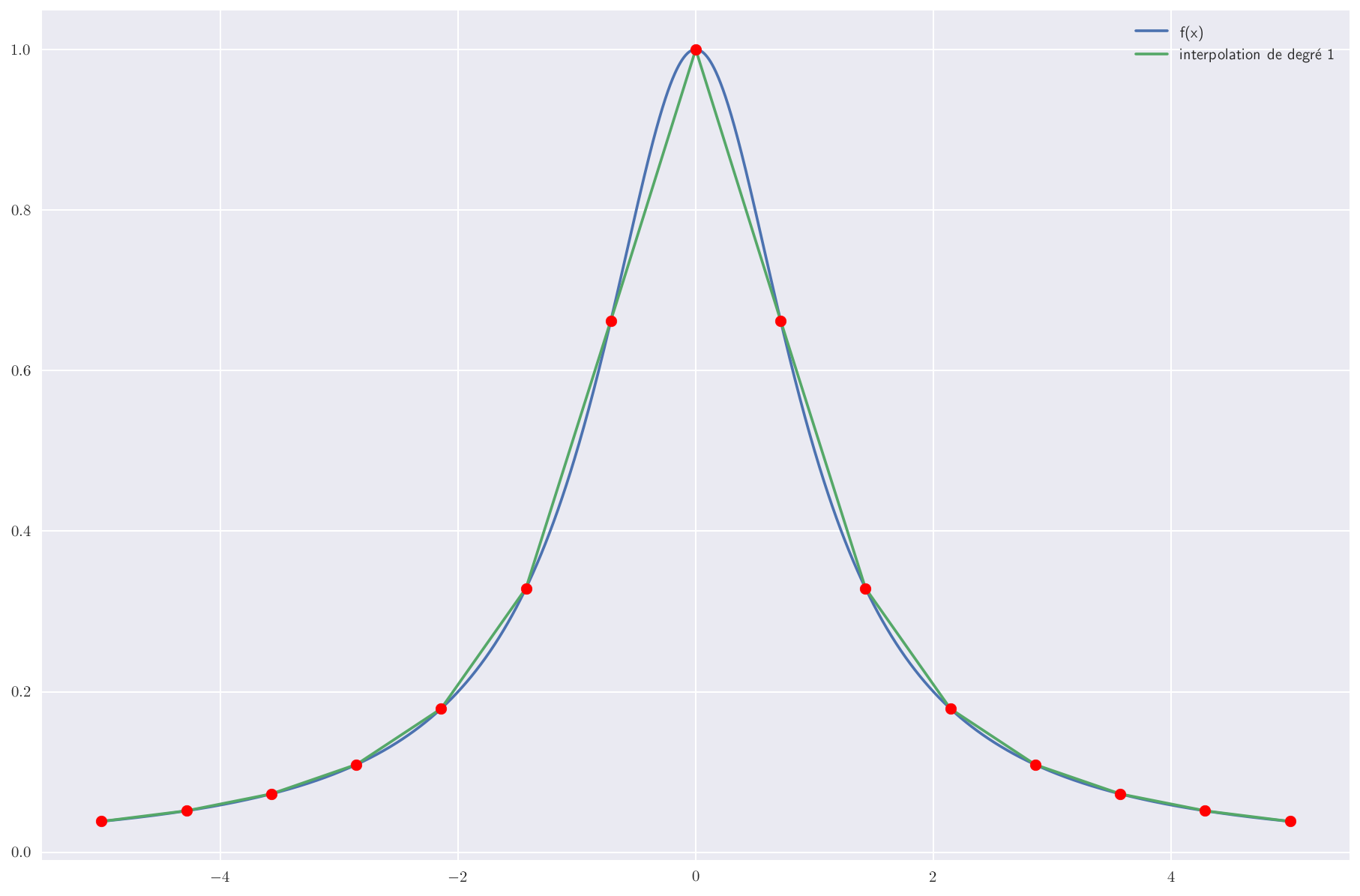
Degré 1

On considère maintenant les deux extrémités de chaque intervalle et on interpole par une loi affine :

def interp_lin(f,interv,N,x):
    debut,fin = interv[0],interv[1]
    X = [debut + i*(fin-debut)/(N-1) for i in range(N)]
    for i in range(N-1):
        if X[i] <= x < X[i+1]:
            return f(X[i])+(x-X[i])*(f(X[i+1])-f(X[i]))/(X[i+1]-X[i])

nb = 2000
N = 15
intervalle = (-5,5)
X = [intervalle[0] + (intervalle[1]-intervalle[0])*i/nb for i in range(nb)]
Y1 = [f(x) for x in X]
Y2 = [interp_lin(f,intervalle,N,x) for x in X]
plt.plot(X,Y1,label = "f(x)")
plt.plot(X,Y2,label = "interpolation de degré 1")
Noeuds = [intervalle[0] + (intervalle[1]-intervalle[0])*i/(N-1) for i in range(N)]
f_noeuds = [f(n) for n in Noeuds]
plt.scatter(Noeuds,f_noeuds,c='r',zorder=3)
plt.legend()

Degré 2

À vous de jouer pour construire la fonction d’interpolation par morceaux de degré 2.
On prendra systématiqement 2 intervalles successifs pour obtenir les 3 points à interpoler. Attention à ce que les morceaux successifs ne se superposent pas (au morceau constitué des 3 nœuds situés aux abscisses $\left(x_0 + i\times\frac{I}{N},x_0 + (i+1)\times\frac{I}{N},x_0 + (i+2)\times\frac{I}{N}\right)$ devra succéder un morceau constitué des 3 nœuds $\left(x_0 + (i+2)\times\frac{I}{N},x_0 + (i+3)\times\frac{I}{N},x_0 + (i+4)\times\frac{I}{N}\right)$ (en appelant $I$ l’intervalle).
On utilisera dans le code la fonction interp (définie plus haut) sur les 3 points du morceau.

def interp_quad(f,interv,N,x):
    debut,fin = interv[0],interv[1]
    X = [debut + i*(fin-debut)/(N-1) for i in range(N)]
    # VOTRE CODE

Correction (cliquer pour afficher)

def interp_quad(f,interv,N,x):
    debut,fin = interv[0],interv[1]
    X = [debut + i*(fin-debut)/(N-1) for i in range(N)]
    for i in range(0,N-2,2):
        if X[i] <= x < X[i+2]:
            return interp(f,3,(X[i],X[i+2]),x)

nb = 2000
N = 15
intervalle = (-5,5)
X = [intervalle[0] + (intervalle[1]-intervalle[0])*i/nb for i in range(nb)]
Y1 = [f(x) for x in X]
Y2 = [interp_quad(f,intervalle,N,x) for x in X]
plt.plot(X,Y1,label = "f(x)")
plt.plot(X,Y2,label = "interpolation de degré 2")
Noeuds = [intervalle[0] + (intervalle[1]-intervalle[0])*i/(N-1) for i in range(N)]
f_noeuds = [f(n) for n in Noeuds]
plt.scatter(Noeuds,f_noeuds,c='r',zorder=3)
plt.legend()

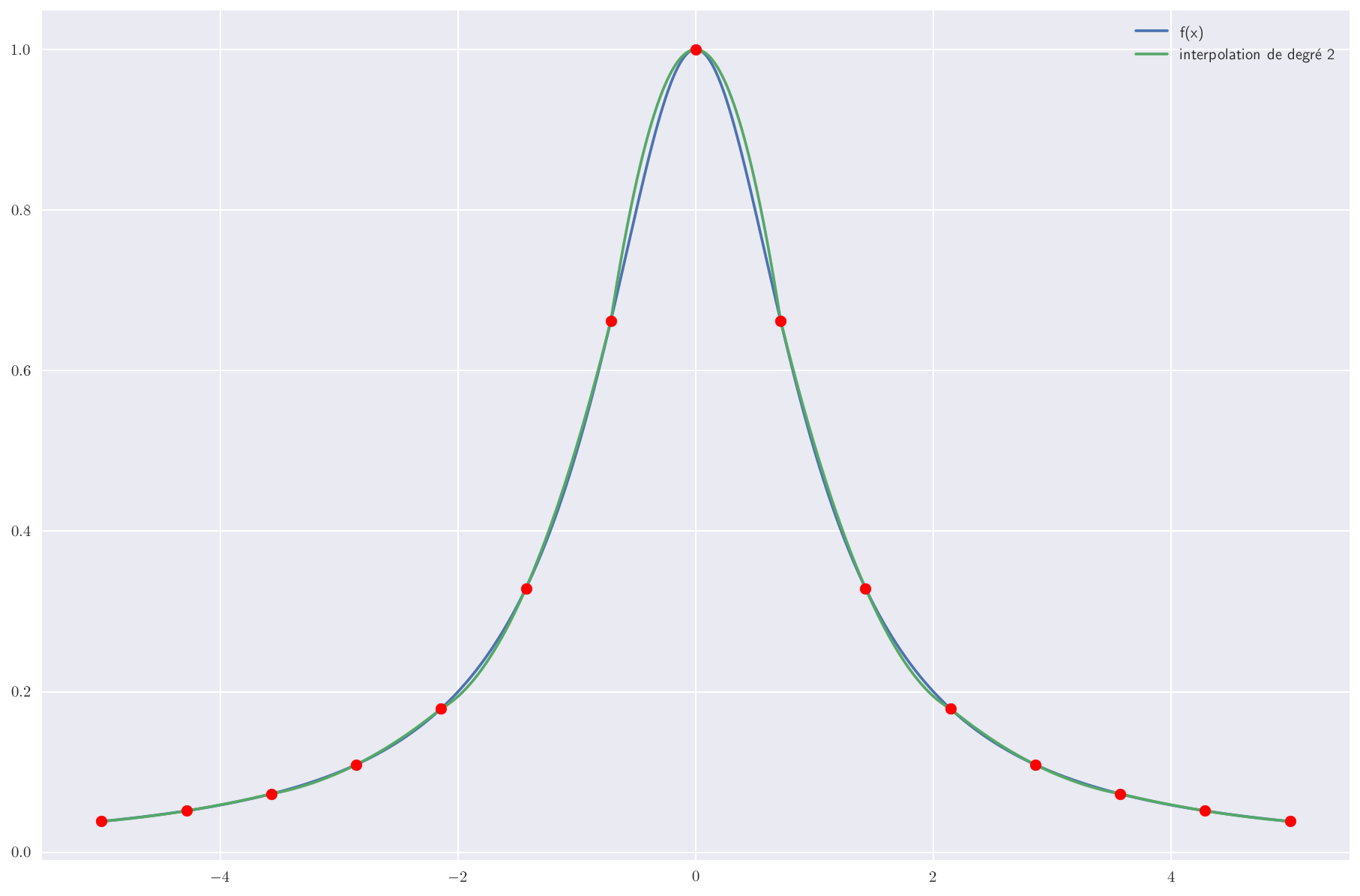
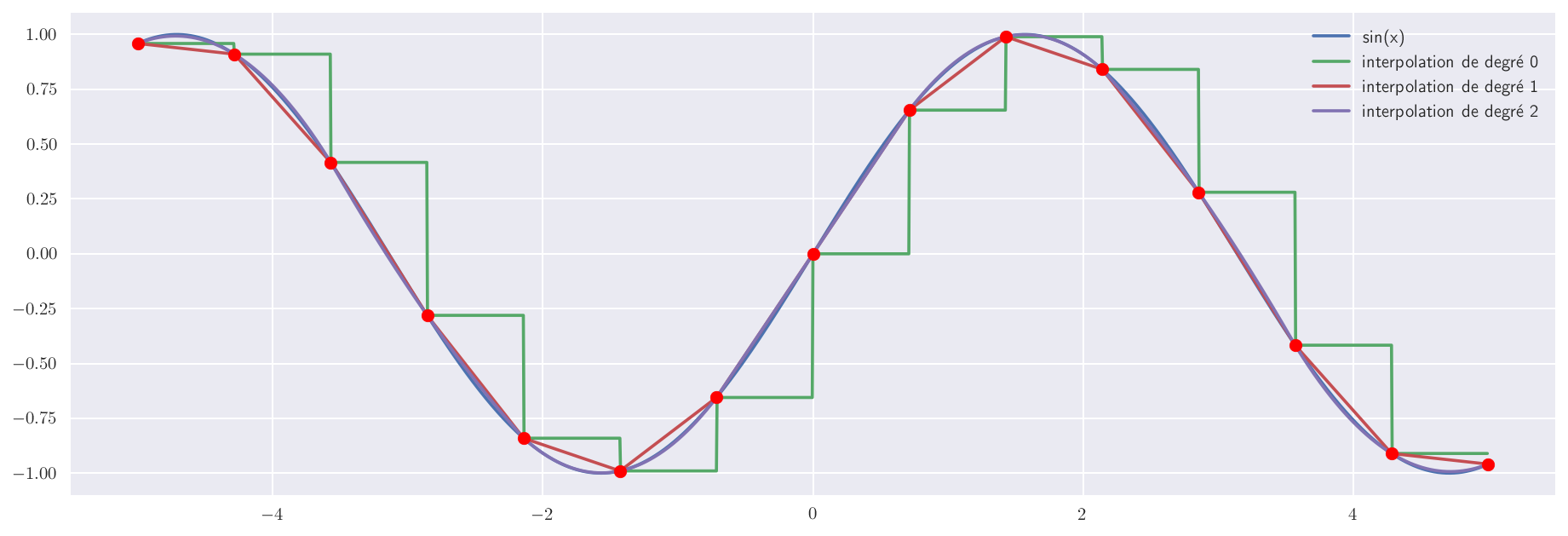
Regardons enfin comment ces trois interpolations s’en sortent pour reproduire d’abord la fonction sinus, puis la fonction de Heaviside.

plt.rcParams['figure.figsize'] = (15, 5)
from math import sin
def h(x):
    return sin(x)
nb = 2000
N = 15
intervalle = (-5,5)
X = [intervalle[0] + (intervalle[1]-intervalle[0])*i/nb for i in range(nb)]
Y1 = [h(x) for x in X]
Y2 = [interp_rect(h,intervalle,N,x) for x in X]
Y3 = [interp_lin(h,intervalle,N,x) for x in X]
Y4 = [interp_quad(h,intervalle,N,x) for x in X]
plt.plot(X,Y1,label = "sin(x)")
plt.plot(X,Y2,label = "interpolation de degré 0")
plt.plot(X,Y3,label = "interpolation de degré 1")
plt.plot(X,Y4,label = "interpolation de degré 2", ls="--")
Noeuds = [intervalle[0] + (intervalle[1]-intervalle[0])*i/(N-1) for i in range(N)]
f_noeuds = [h(n) for n in Noeuds]
plt.scatter(Noeuds,f_noeuds,c='r',zorder=3)
plt.legend()

def h(x):
    if x >= 0:
        return 1
    else:
        return 0
nb = 2000
N = 15
intervalle = (-5,5)
X = [intervalle[0] + (intervalle[1]-intervalle[0])*i/nb for i in range(nb)]
Y1 = [h(x) for x in X]
Y2 = [interp_rect(h,intervalle,N,x) for x in X]
Y3 = [interp_lin(h,intervalle,N,x) for x in X]
Y4 = [interp_quad(h,intervalle,N,x) for x in X]
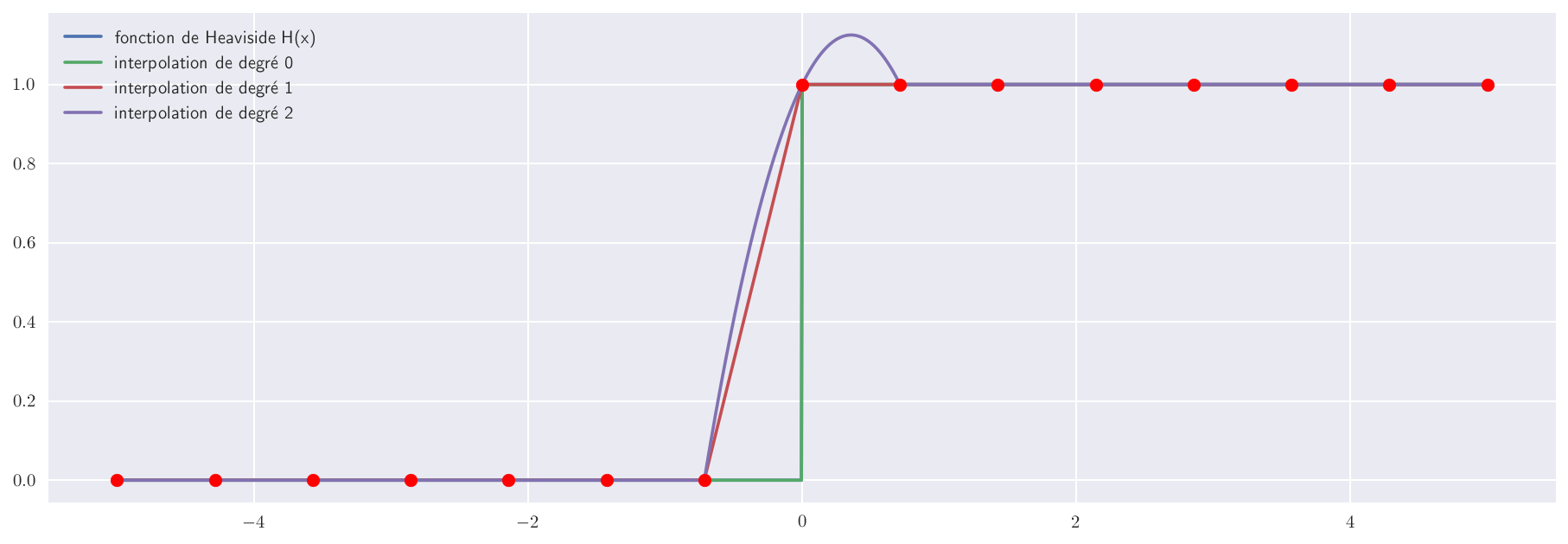
plt.plot(X,Y1,label = "fonction de Heaviside H(x)")
plt.plot(X,Y2,label = "interpolation de degré 0", ls = "--")
plt.plot(X,Y3,label = "interpolation de degré 1")
plt.plot(X,Y4,label = "interpolation de degré 2")
Noeuds = [intervalle[0] + (intervalle[1]-intervalle[0])*i/(N-1) for i in range(N)]
f_noeuds = [h(n) for n in Noeuds]
plt.scatter(Noeuds,f_noeuds,c='r',zorder=3)
plt.legend()

Méthode d’Euler

Présentation

Complétez la fonction Euler ci-dessous qui implémente la méthode d’Euler explicite permettant de résoudre les équations différentielles du premier ordre : $$\begin{cases}y’(t)=f(t,y(t))\\y(t_0)=y_0\end{cases}$$

def Euler(f,t0,tf,y0,h):
    """
    postconditions: T est la liste des ti et Y est la liste des valeurs yi=y(ti)
    """
    n = int((tf-t0)/h)
    T = [t0+i*h for i in range(n)]
    # VOTRE CODE
    return T,Y

Correction (cliquer pour afficher)

def Euler(f,t0,tf,y0,h):
    n = int((tf-t0)/h)
    T = [t0+i*h for i in range(n)]
    Y = [y0]
    for i in range(1,n):
        Y.append(Y[i-1]+h*f(T[i-1],Y[i-1]))
    return T,Y

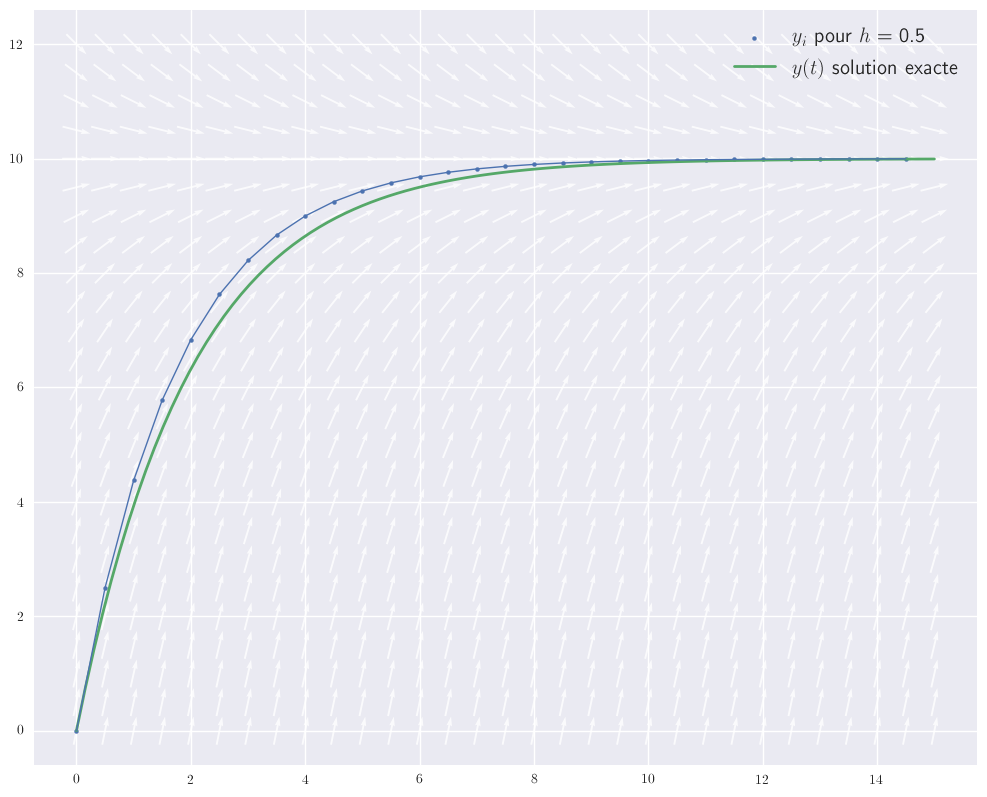
Testons notre fonction.
La cellule ci-dessous définit la dérivée de $f(t)$ et les deux cellules qui suivent permettent de tracer le résultat.
Libre à vous de modifier f et les autres paramètres (le pas en particulier) pour expérimenter.

def f(t,y): 
    return 5-y/2

import matplotlib.pyplot as plt
import numpy as np
plt.style.use('seaborn')
params = {'axes.titlesize': 'xx-large',
          'legend.fontsize': 15,
          'text.usetex': True,
          'figure.dpi': 150,
          'figure.figsize': (20,10)}
plt.rcParams.update(params)

tmin, tmax = 0, 15
ymin, ymax = 0, 12

nbfl = 2
fig, ax = plt.subplots()
ax.set_aspect('equal')
T,Y = np.meshgrid(np.linspace(tmin,tmax,nbfl*(tmax-tmin)+1),np.linspace(ymin,ymax,nbfl*(ymax-ymin)+1))
U = 1
V = f(T,Y)
N = np.sqrt(U**2+V**2)
U2, V2 = U/N, V/N
ax.quiver(T,Y,U2,V2,pivot='mid',width=0.002,scale_units='xy',scale=2,alpha=0.8,color="white",units='width')

pas = 0.5 # pas
y0 = 0
T,Y = Euler(f,tmin,tmax,y0,pas)

ax.plot(T,Y,lw=1)
ax.scatter(T,Y,s=8,label=r"$y_i$ pour $h=$"+f" {pas}")
Tsol = np.linspace(0,15,100)
Ysol = 10*(1-np.exp(-Tsol/2))
ax.plot(Tsol,Ysol,ls="-",lw=2,zorder=1,label=r"$y(t)$ solution exacte")
plt.legend()

png

def acc(t):
    if 2 <= t <= 4:
        return 4
    elif 4 < t <= 8:
        return -2
    elif 10 < t <= 11:
        return -4
    elif 11 < t <= 13:
        return 2
    else:
        return 0

Imaginons que la fonction acc ci-dessus corresponde à la commande de l’accélération d’un ascenceur.
Déterminons la position de l’ascenceur au cours du temps.

t0, tmax = 0, 14
v0 = 0
y0 = 2
t, v, y = t0, v0, x0
T, V, Y = [t0],[v0],[y0]
dt = 1e-3
while t < tmax:
    v += acc(t)*dt
    y += v*dt
    t += dt
    T.append(t)
    V.append(v)
    Y.append(y)

Quelle méthode d’intégration a-t-elle été mise en œuvre dans le code ci-dessus ?

a : méthode d’Euler explicite
b: méthode d’Euler implicite
c : méthode d’Euler semi-implicite
d : méthode d’Euler améliorée

Correction (cliquer pour afficher)

On a un mixe dans les mises à jours de $v$ et de $y$ entre l'utilisation de valeurs aux instants $t$ ou $t+dt$ :
$v(t+dt) = v(t)+a(\color{orange}t\color{#006C65})\times dt$
$y(t+dt) = y(t) + v(\color{red}t+dt\color{#006C65})\times dt$.
Il s'agit donc de la méthode semi-explicite.

Imaginons qu’un pallier fasse 6 m et que le point de départ de l’ascenceur corresponde au RDC (étage 0), quels sont les 2 autres étages visités par l’ascenceur ?

Correction (cliquer pour afficher)

On peut tracer l'évolution de $y(t)$ pour nous aider grâce à cette ligne :
plt.plot(T,Y)
On obtient : L'ascenceur s'est donc arrêté aux étages 4 et 3.

La dernière mission est d’intégrer le système d’équations différentielles du premier ordre suivant pour $t$ allant de 0 à 100 : $$\begin{cases}x’=\sigma(y-x)\\y’=\rho x-y-xz\\z’=xy-\beta \end{cases}$$ on prendra : $$\begin{cases}\sigma = 3\\\rho = 26.5\\\beta = 1\end{cases}$$ et $(x_0;y_0;z_0)=(0;1;1,05)$.

Vous utiliserez la méthode d’Euler explicite et prendrez un pas de $0,01$.
Votre code devra produire les 3 listes de 10001 éléments contenant les valeurs $x(t_i),y(t_i),z(t_i)$ pour chaque $t_i \in [0,100]$ et elles devront être nommées (pour faire original) X, Y et Z.

Correction (cliquer pour afficher)

s,r,b = 3,26.5,1
x0,y0,z0 = 0,1,1.05
t = 0
h = 1e-2
x,y,z = x0,y0,z0
X,Y,Z = [x0],[y0],[z0]
while t <= 100:
    x_old, y_old, z_old = x,y,z
    x += (s*(y_old-x_old))*h
    y += (r*x_old - y_old - x_old*z_old)*h
    z += (x_old*y_old - b*z_old)*h
    X.append(x)
    Y.append(y)
    Z.append(z)
    t += h

import plotly.graph_objects as go
fig = go.Figure(data=go.Scatter3d(x=X,y=Y,z=Z,mode="lines",line=dict(color='darkblue',width=2)))
fig.update_layout(scene = dict(xaxis = dict(showbackground=False,showticklabels=False,title=''),yaxis = dict(showbackground=False,showticklabels=False,title=''),zaxis = dict(showbackground=False,showticklabels=False,title='')))
fig.show()