TP 13 : Algorithmes pour l’intelligence artificielle
Cliquez sur cette invitation pour récupérer le repository du TP.
Algorithme des k plus proches voisins
Interpolation
Construisons un jeu de données entâché de bruit :
import matplotlib.pyplot as plt
plt.style.use('seaborn')
params = {'figure.figsize': (15, 10),
'axes.titlesize': 'xx-large',
'figure.dpi' : 150}
plt.rcParams.update(params)
from random import random
from math import pi,cos
X = []
Y = []
N = 400
for i in range(N):
x = pi*random()-pi/2
X.append(x)
y = cos(x+0.1*(random()-0.5))+0.2*(random()-0.5)
Y.append(y)
Pts = list(zip(X,Y))
plt.scatter(*zip(*Pts)) # zip(*zip(L1,L2)) redonne un objet composé de L1 et L2 et * le déballe
Mettez maintenant au point une fonction
KNN_interpayant pour paramètre le nombre de voisins à considérer $k$, les données d’apprentissage sous la forme d’une liste et l’abscisse de la nouvelle donnée dont on cherche l’ordonnée.
Elle retourne l’ordonnée de la nouvelle donnée en prenant la moyenne des $k$ ordonnées les plus proches. Votre fonction pourra utiliser la méthode nativesortqui trie en place une listeL(la liste triée s’obtient grâce àL.sort()).
def KNN_interp(x: float, k: int, Pts: list) -> float:
"""
préconditions: Pts est une liste de tuples contenant les coordonnées (x,y) des points d'entraînement
postcondition: la fonction retourne la moyenne des ordonnées des k points dont l'abscisse est la plus proche de x
"""
### VOTRE CODE
Correction (cliquer pour afficher)
def KNN_interp(x,k,Pts): Nv_Pts = [] for pt in Pts: Nv_Pts.append((abs(pt[0]-x),pt[1])) y = 0 Nv_Pts.sort() for pt in Nv_Pts[:k]: y += pt[1] y /= k return y
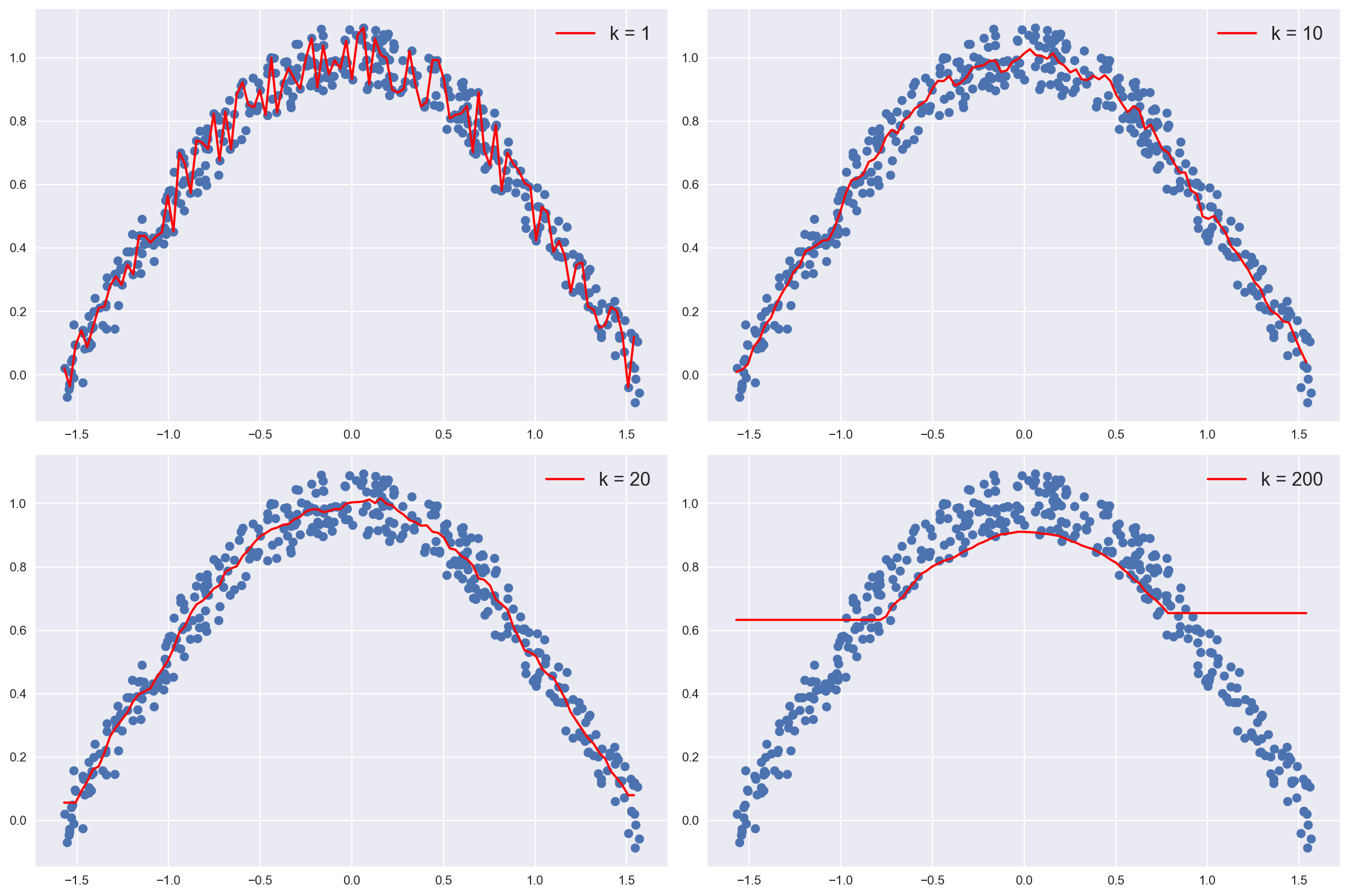
fig, axs = plt.subplots(2, 2)
K = [1,10,20,200]
N = 100
X = [-pi/2+pi/N*i for i in range(N)]
i = 0
for k in K:
Y = []
for x in X:
Y.append(KNN_interp(x,k,Pts))
axs[i//2,i%2].plot(X,Y,c='r',label=f'k = {k}')
axs[i//2,i%2].scatter(*zip(*Pts))
axs[i//2,i%2].legend(fontsize = 15)
i += 1
plt.tight_layout()
Classification
La grande majorité du temps, lorsque l’on parle de la distance entre deux points, on sous-entend la distance euclidienne. Mais ce n’est pas la seule définition possible de la distance.
Dans le cas d’un monde quadrillé comme les rues des villes américaines, divisées par blocs, la distance de Manhattan est plus appropriée.
- Distance euclidienne $d_E(x,y)$ entre le points $x = (x_1,x_2,\ldots,x_n)$ et le points $y = (y_1,y_2,\ldots,y_n)$ : $$d_E(x,y) = \sqrt{(y_1-x_1)^2+(y_2-x_2)^2+\cdots+(y_n-x_n)^2}$$
- Distance de Manhattan $d_M(x,y)$ entre le points $x = (x_1,x_2,\ldots,x_n)$ et le points $y = (y_1,y_2,\ldots,y_n)$ : $$d_M(x,y) = |y_1-x_1|+|y_2-x_2|+\cdots+|y_n-x_n|$$
Que vaut la distance euclidienne et la distance de Manhattan entre $A$ et $B$ dans la figure ci-dessus ?

Correction (cliquer pour afficher)
dE = 15 (hypoténuse d'un triangle reglangle de côtés 9 et 12)
dM = 21
Existe-t-il plusieurs chemins différents ayant la même distance euclidienne ?
Correction (cliquer pour afficher)
Plein (combien ?)
Existe-t-il plusieurs chemins différents ayant la même distance de Manhattan ?
Correction (cliquer pour afficher)
Non, un seul (le segment de droite entre A et B).
On utilisera dans la suite la distance euclidienne.
Construisez une fonction
distprenant en paramètre les coordonnées d’un point $x$ et les coordonnées d’autres points sous la forme d’une liste et qui retourne la liste des distances entre $x$ et les $n$ autres points.
Vous assurerez par unassertque tous les points ont bien le même nombre de coordonnées.
def dist(x: list, Pts: list) -> list:
"""
préconditions: x contient les coordonnées d'un point
Pts est une liste de tuples ou chaque tuple contient les coordonnées d'un point
tous les points doivent avoir le même nombre de coordonnées
postcondition: la fonction doit retourner la liste des distances entre le points x et chacun des points de la liste Pts.
"""
### VOTRE CODE
Correction (cliquer pour afficher)
def dist(x,Pts): n = len(x) for pt in Pts: assert n == len(pt), "Les points n'ont pas tous le même nombre de coordonnées !" L = [] for pt in Pts: d = 0 for i in range(n): d += (pt[i]-x[i])**2 d = d**0.5 L.append(d) return L
On va se servir d’un jeu de données célèbre pour tester l’algorithme KNN : un extrait de la MNIST database contenant des images carrées (8 pixels sur 8 pixels) de chiffres écrits à la main, accompagnés de leur étiquette (le chiffre sensé être représenté sur l’image).
from sklearn.datasets import load_digits
digits = load_digits()
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1)).astype(int)
data = list(map(list,data))
labels = list(digits.target)
Chacune des images a été applatie, c’est-à-dire qu’on les a réduites à une liste unidimensionnelle de 64 entiers entre 0 et 255.
data contient une liste de 1797 images qui sont donc chacune une liste de 64 valeurs.
labels contient les étiquettes correspondantes (dans le même ordre).
Construisez une fonction capable de transformer une liste de 64 valeurs en une matrice $8\times 8$ :
def lignetomatrice(liste64: list) -> list:
"""
posctconditions: la liste retournée doit être de dimensions 2 et de format 8*8
"""
### VOTRE CODE
Correction (cliquer pour afficher)
def lignetomatrice(liste64): mat = [] for j in range(64): if j%8 == 0: mat.append([]) mat[-1].append(liste64[j]) return mat
Visualisons quelques unes des images grâce aux lignes suivantes et ajoutons le label comme titre à l’image :
fig, axs = plt.subplots(2, 5)
i = 0
for ax in axs.flat:
image64 = data[i]
image88 = lignetomatrice(image64)
ax.imshow(image88, interpolation='nearest', cmap='Greys')
ax.set_title(f'{labels[i]}')
ax.axis('off')
i += 1
plt.tight_layout()
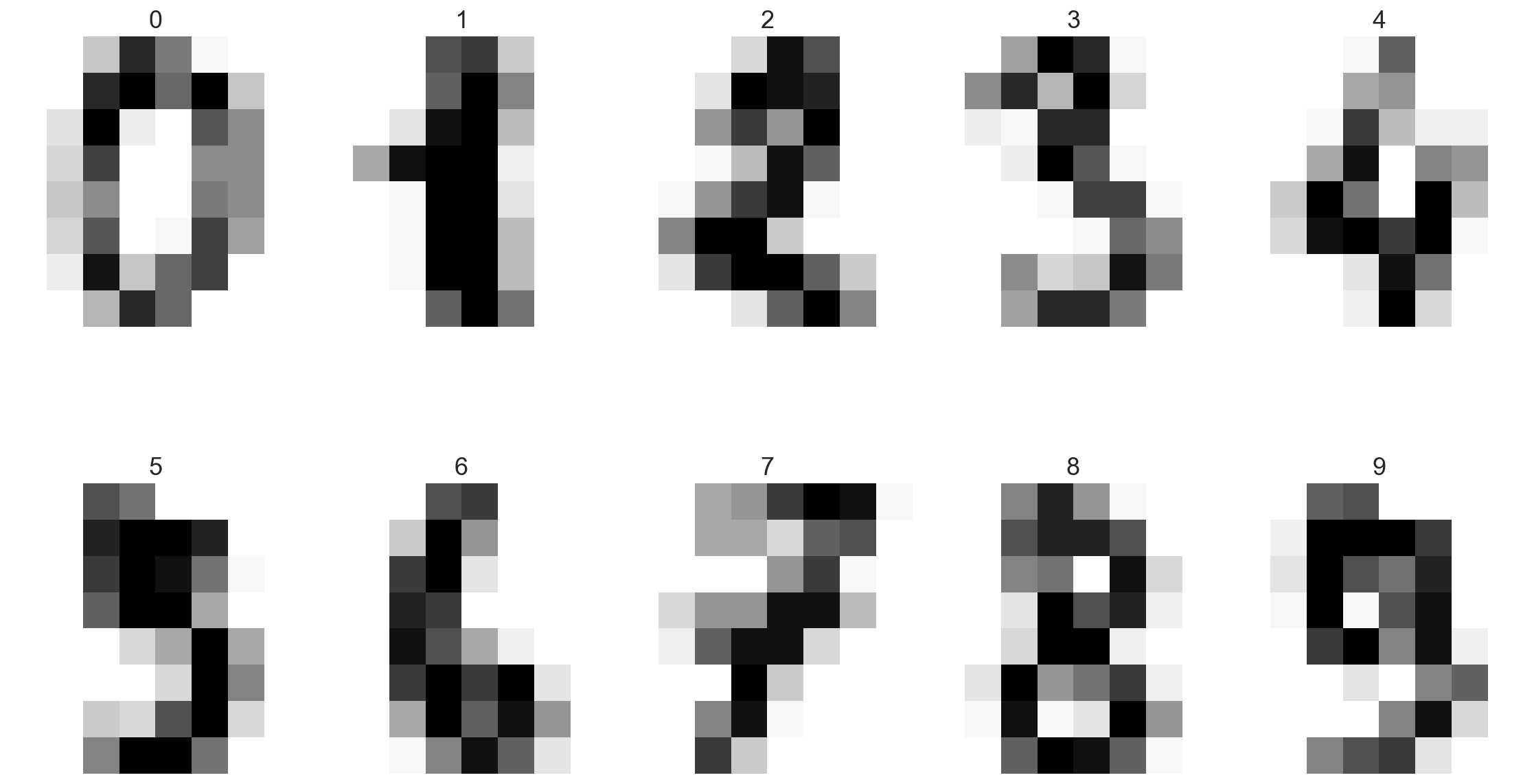
On va séparé le jeu de données en deux, une moitié pour nous servir pour l’apprentissage et l’autre pour tester.
n = len(data)
data_appr = data[:n//2]
labels_appr = labels[:n//2]
data_test = data[n//2:]
labels_test = labels[n//2:]
C’est le moment de construire une fonction
KNN_clasprenant en paramètre une image (liste de 64 flottants), l’entier $k$ du nombre de voisins à considérer, la liste des données servant à l’apprentissage et la liste des étiquettes (dans le même ordre) et qui retourne un entier entre 0 et 9 correspondant au mode (étiquette la plus représentée) des k plus proches voisins.
Votre fonction devra utiliser la fonctiondist.
Pour calculer le mode d’une listeL, vous utiliserezmodedu module statistics.
Aide : une liste de listes ou de tuples est triée en fonction du premier élément de la sous-liste ou du tuple.
from scipy import stats
def KNN_class(X: list, k: int, Appr: list, Etiq: list) -> list:
"""
préconditions: X est l'image dont on veut déterminer l'étiquette
Appr est l'ensemble des données d'apprentissage, c'est une liste de listes,
chacune de ces liste correspond à une image
Etiq est une liste d'entiers correspondant aux étiquettes de chaque image.
postconditions: la fonction doit retourner l'étiquette la plus fréquente (mode) parmi les k images les plus proches
"""
### VOTRE CODE
Correction (cliquer pour afficher)
import statistics as stat def KNN_class(X,k,Appr,Etiq): L = dist(X,Appr) LplusEtiq = [] for i in range(len(L)): LplusEtiq.append((L[i],Etiq[i])) LplusEtiq.sort() EtiqFin = [] for e in LplusEtiq[:k]: EtiqFin.append(e[1]) return stat.mode(EtiqFin)
Validation
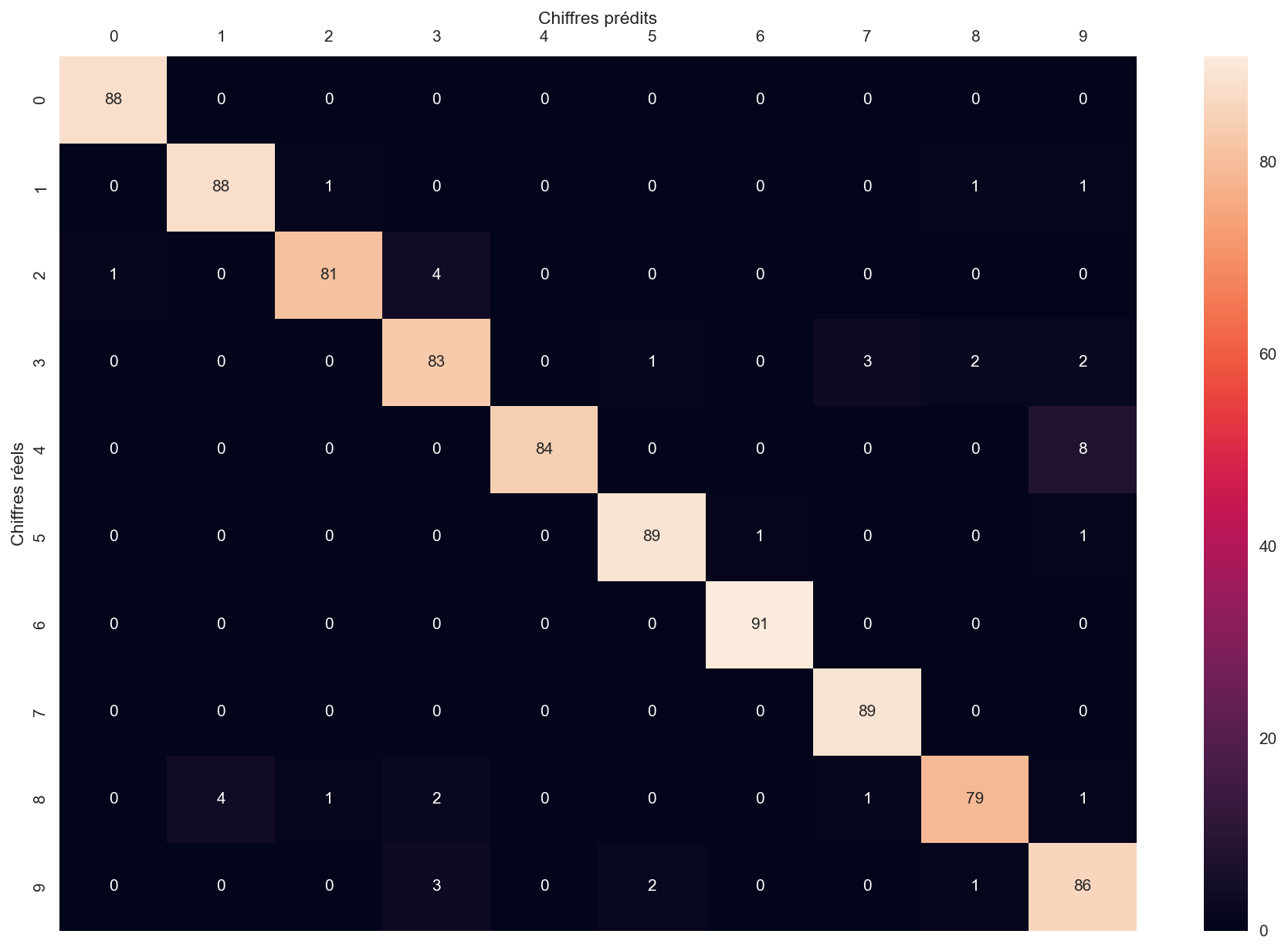
La matrice de confusion va nous aider à évaluer notre algorithme de classification.
Commençons par construire une matrice carrée $10\times 10$ dont les lignes correspondent aux étiquettes réelles et les colonnes aux étiquettes prédites.
On va prendre k = 8 (comme ça, au hasard…).
Rq : la cellule met environ 25 s à s’exécuter.
M = [[0 for j in range(10)] for i in range(10)]
k = 8
for m in range(len(data_test)) :
i = labels_test[m]
j = KNN_class(data_test[m],k,data_appr,labels_appr)
M[i][j] += 1
import seaborn as sns
s = sns.heatmap(M,annot=True)
s.set(xlabel='Chiffres prédits', ylabel='Chiffres réels')
s.xaxis.tick_top()
s.xaxis.set_label_position('top')
À partir de cette matrice générale, construisez la matrice de confusion pour le chiffre 3. La matrice comprend les valeurs suivantes :
- vrais positifs VP
- vrais négatifs VN
- faux positifs FP
- faux négatifs FN
# La matrice de confusion Mc3 devra avoir la forme [[VP,FP],[FN,VN]]
# Les valeurs VP,FP,FN,VN sont des entiers correspondant aux effectifs dans chaque catégorie
# Attention : vos calculs doivent pouvoir s'adapter automatiquement à une autre matrice M !!
### VOTRE CODE
Mc3 = [[VP,FN],[FP,VN]]
Correction (cliquer pour afficher)
# VP : chiffres prédits comme 3 et qui sont des 3 VP = M[3][3] # FP : chiffre qui sont prédits comme des 3 mais qui n'en sont pas FP = sum([M[i][3] for i in range(len(M)) if i != 3]) # VN : chiffres prédits comme autre chose que des 3 et qui sont bien autre chose VN = sum([sum([M[i][j] for j in range(len(M)) if j != 3]) for i in range(len(M)) if i!= 3]) # FN : chiffres qui sont prédits comme autre chose que des 3 mais qui en sont FN = sum([sum([M[i][j] for j in range(len(M)) if j != 3]) for i in range(len(M)) if i== 3])
n = len(data_test)
labels = [[f'VP\n{VP}\n{VP/n:.1%}',f'FN\n{FN}\n{FN/n:.1%}'],[f'FP\n{FP}\n{FP/n:.1%}',f'VN\n{VN}\n{VN/n:.1%}']]
x_axis_labels = ['Positif','Négatif']
y_axis_labels = ['Positif','Négatif']
s = sns.heatmap(Mc3,annot=labels,fmt='',annot_kws={"size": 18})
s.set_xticklabels(x_axis_labels, fontsize=10)
s.set_yticklabels(y_axis_labels, fontsize=10)
s.xaxis.tick_top()
s.xaxis.set_label_position('top')
s.set_xlabel('Chiffres 3 prédits', fontsize=15)
s.set_ylabel('Chiffres 3 réels', fontsize=15)
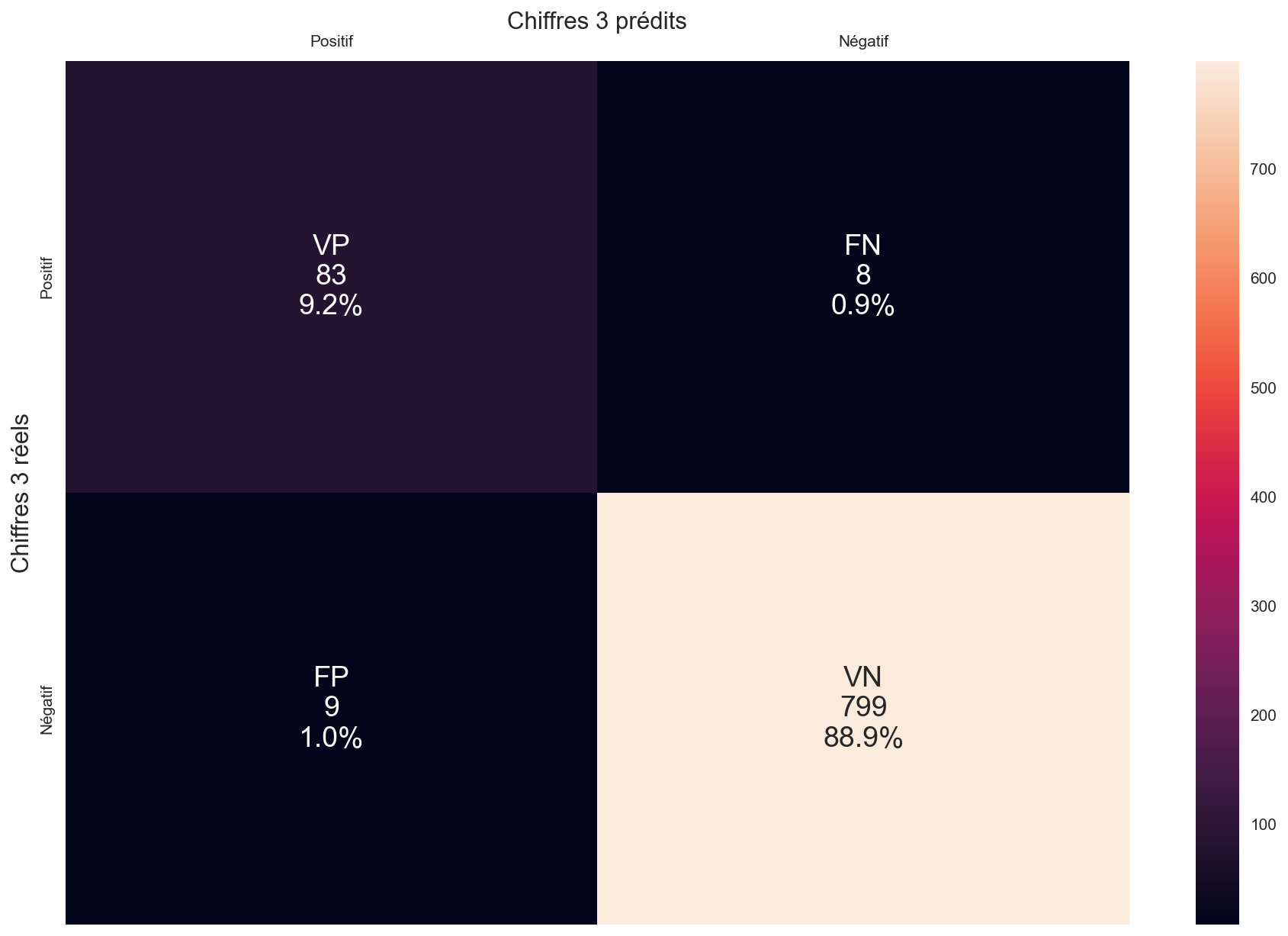
Que peut-on dire des talents de classificateur de notre algorithme pour ce qui est du chiffre 4 (attention, on ne parle plus du chiffre 3) :
- a : il est plus sensible que précis (rappel > précision)
- b : il est plus précis que sensible (précision > rappel)
Correction (cliquer pour afficher)
La matrice de confusion nous montre que :Donc pour le chiffre 4, l'algo est plus précis que sensible.
- Parmi les 86 "4" prédits, tous sont bien des 4 $\Rightarrow$ précision de 100%
- Parmi tous les vrais "4" (92), 8 sont prédits comme étant autre chose (à chaque fois des 9...) $\Rightarrow$ rappel de 87,0%
Calculez enfin l’exactitude totale de l’algorithme sur les 899 images testées.
Correction (cliquer pour afficher)
On obtient l'exactitude en sommant les éléments dans la diagonale :
val2 = sum([M[i][i] for i in range(len(M))])/len(datatest)
On obtient 95,4%.
Des librairies dédiées contenant des algorithmes optimisés permettent de grandement accélérer les choses.
Ici, on va utiliser scikit-learn qui s’appuie grandement sur numpy, lui-même principalement écrit en C.

from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors=8) # n_neighbors correspond à la valeur k
model.fit(data_appr, labels_appr)
predictions = model.predict(data_test) # predictions est la liste des prédictions pour chaque image dans data_test
M = [[0 for j in range(10)] for i in range(10)]
for m in range(len(data_test)) :
i = labels_test[m]
j = predictions[m]
M[i][j] += 1
sns.heatmap(M,annot=True)
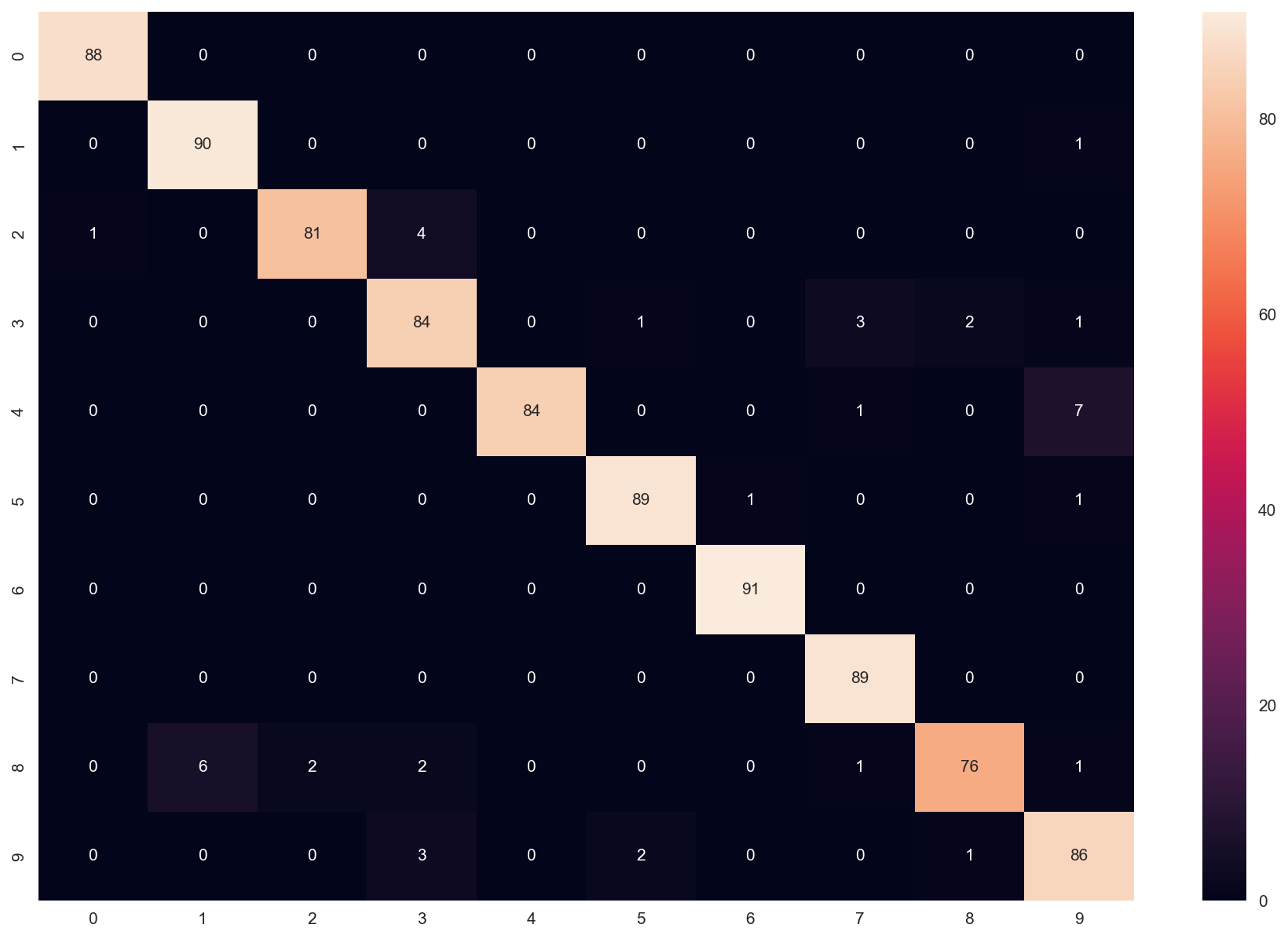
Commentaire (cliquer pour afficher)
Les petites différences observées viennent de l'algorithme utilisé pour donner le mode statistique de la liste des chiffres prédits. Quel résultat donne-t-il quand il y a plusieurs modes possibles en concurrence (deux étiquettes majoritaires présentes autant de fois l'une que l'autre par exemple) ? Suivant son choix, les résultats diffèrent. Et visiblement le mode du modulestatisticsne fait pas les mêmes choix que le mode utilisé parscikit-learn.
Cherchons maintenant la valeur optimale de k, celle qui optimise l’exactitude.
Pour cela, et par souci de rapidité, on va utiliser l’implémentation de la librairiescikit-learnci-dessus.
n = len(data_test)
K = [i for i in range(1,50)]
Exa = []
for k in range(1,50):
model = KNeighborsClassifier(n_neighbors=k)
model.fit(data_appr, labels_appr)
predictions = model.predict(data_test)
M = [[0 for j in range(10)] for i in range(10)]
for m in range(len(data_test)):
i = labels_test[m]
j = predictions[m]
M[i][j] += 1
Exa.append(sum([M[i][i] for i in range(10)])/n)
plt.plot(K,Exa)
plt.xlabel('k')
plt.ylabel('exactitude')
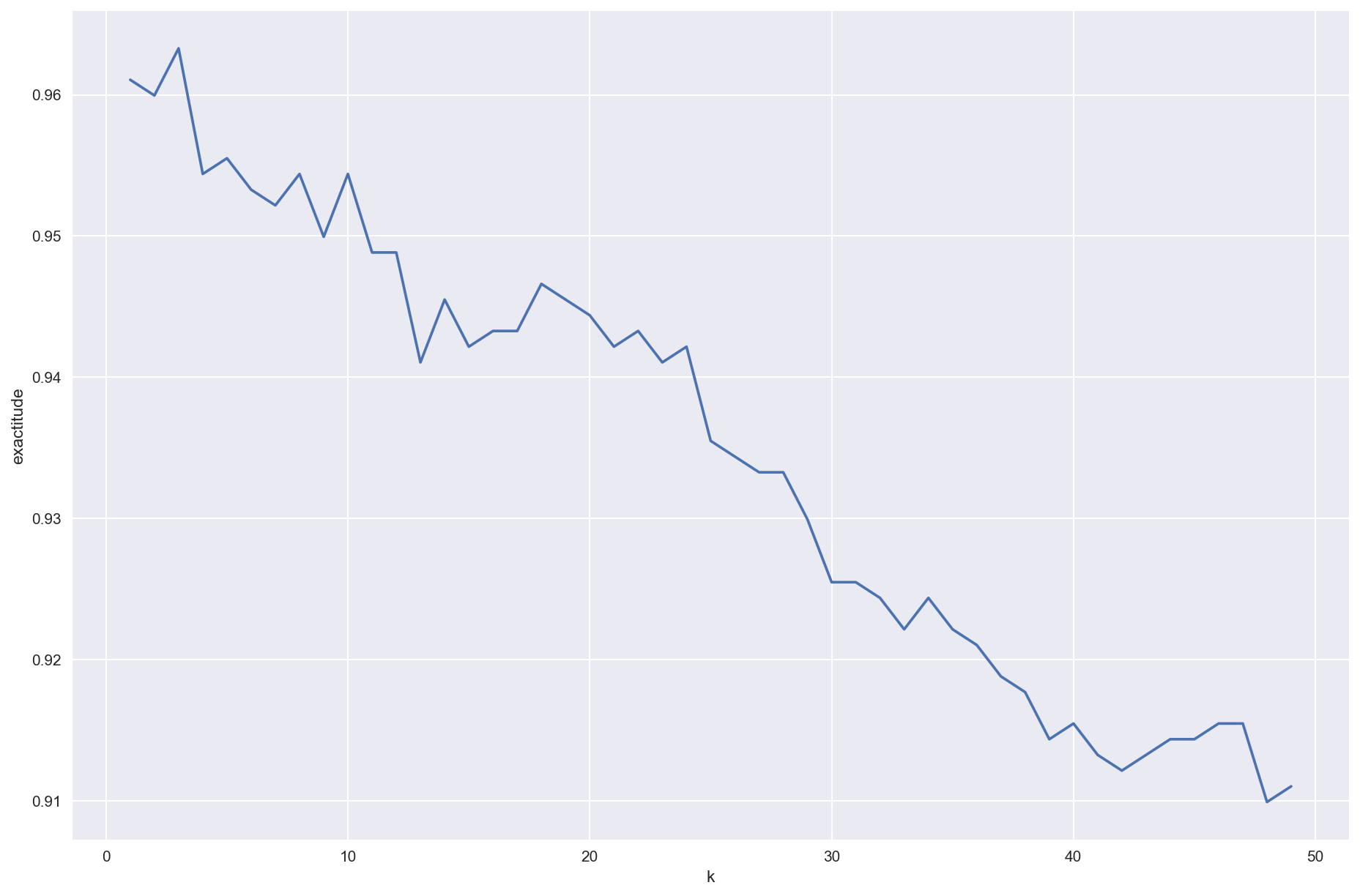
Correction (cliquer pour afficher)
$k=3$ optimise l'exactitude.
Algorithme des k moyennes
from random import random
import matplotlib.pyplot as plt
plt.style.use('seaborn')
params = {'figure.figsize': (15, 10),
'axes.titlesize': 'xx-large',
'figure.dpi' : 150}
plt.rcParams.update(params)
def kmoyennes(k: int, data: list) -> list:
n = len(data)
dim = len(data[0])
itermax = 100
itgenmax = 10
assert n > k, "plus de clusters que de points de données..."
itgen = 0
distancemin = float('inf')
sauvegarde_presente = False
while itgen < itgenmax:
test = True
iteration = 1
# initialisation aléatoire des k centres
Centres = initialisation(k,data,dim)
# Copie des positions de ces centres pour tester plus loin s'ils ont bougé
Centres_old = []
for e in Centres:
Centres_old.append(e[:]) # on utilise le slicing pour créer un nouvel objet et pas seulement une référence
### coeur de l'algorithme :
while test and (iteration < itermax):
# calcul des distance entre un centre et tous les points de données, pour chaque centre
Dist = []
for i in range(k):
Dist.append(dist(Centres[i],data))
# attribution des données au centre le plus proche
Clusters = attribution(k,data,Dist)
# déplacement du centre au milieu de son cluster
deplacement(k,Clusters,Centres,data)
# si les clusters n'ont pas bougé, test reste faux et on sort du while
test = False
for i in range(k):
if max(dist(Centres[i],[Centres_old[i]])) > 1e-6*max(Dist[i]):
test = True
for i in range(k):
Centres_old[i] = Centres[i][:]
iteration += 1
# on recommence plusieurs fois en calculant à chaque fois l'inertie
# pour ne garder au final que l'itération avec l'inertie la plus petite
# le but est de se prémunir d'un blocage sur une solution suboptimale
itgen += 1
distance = evaluation(k,Clusters,Centres,data)
if distance < distancemin:
distancemin = distance
Clusters_save = Clusters[:] # meilleurs Clusters jusque-là
Centres_save = []
for i in range(k):
Centres_save.append(Centres[i][:]) # meilleurs Centres jusque-là
sauvegarde_presente = True
if sauvegarde_presente:
Clusters = Clusters_save
Centres = Centres_save
return Clusters, Centres
def initialisation(k: int, data: list, dim : int) -> list:
Centres = []
Ampl = []
for d in range(dim):
MA = max([data[i][d] for i in range(len(data))])
MI = min([data[i][d] for i in range(len(data))])
Ampl.append((MI,MA))
for i in range(k):
Centres.append([])
for d in range(dim):
Centres[i].append(Ampl[d][0]+(Ampl[d][1]-Ampl[d][0])*random())
return Centres
def evaluation(k: int, Clusters: list, Centres: list, data: list) -> float:
n = len(data)
distance = 0
for i in range(k):
data_clusters = [data[j] for j in range(n) if Clusters[j] == i]
distance += sum(dist(Centres[i],data_clusters))
return distance
Il manque encore la définition de 2 fonctions utilisées dans
kmoyennes.
Commençons par écrire la fonction permettant d’attribuer un centre à chaque point de données.
def attribution(k: int, data: list, Dist: list) -> list:
"""
préconditions: Dist est une liste à deux dimensions contenant k sous-listes
chaque sous-liste contient les distances de chaque point de data à un des centres
Une sous-liste correspond à un centre
postconditions: la fonction doit retourner (sous forme de liste) le numéro de cluster (de 0 à k-1) associé à chaque point de data
Si le premier point appartient au cluster 1, le deuxième au cluster 3, le troisème au cluster 0,
la liste Clusters commencera ainsi [1,3,0,...]
"""
### VOTRE CODE
Correction (cliquer pour afficher)
def attribution(k,data,Dist): Cluster = [] n = len(data) for m in range(n): imin = 0 mini = Dist[0][m] for i in range(1,k): if Dist[i][m] < mini: mini = Dist[i][m] imin = i Cluster.append(imin) return Cluster
Écrivons maintenant la fonction déplacement qui modifie en place la position des k centres.
def deplacement(k: int, Clusters: list, Centres: list, data: list) -> list:
"""
préconditions: Clusters est une liste du numéro de cluster associé au point à la même position dans data
Centres doit être mutable
postconditions: en sortie, les positions des centres sont mis à jour
et correspondent aux barycentres des points qui leur sont attribués
"""
### VOTRE CODE
Correction (cliquer pour afficher)
def deplacement(k,Clusters,Centres,data): dim = len(data[0]) DataCluster = [] n = len(data) for i in range(k): DataCluster.append([]) for i in range(n): DataCluster[Clusters[i]].append(data[i]) for i in range(k): lcluster = len(DataCluster[i]) if lcluster != 0: for l in range(dim): moy = 0 for j in range(lcluster): moy += DataCluster[i][j][l] moy /= lcluster Centres[i][l] = moy
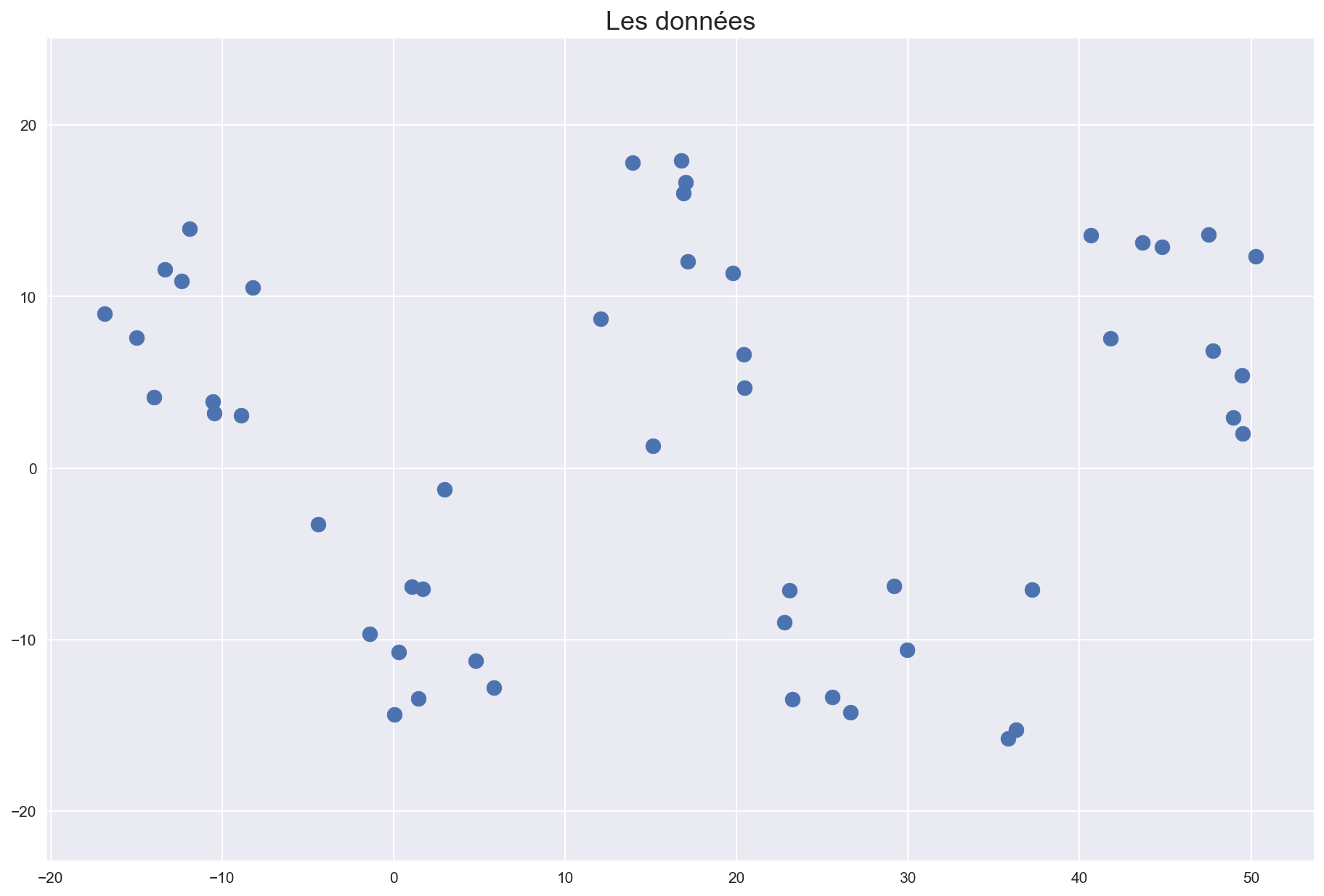
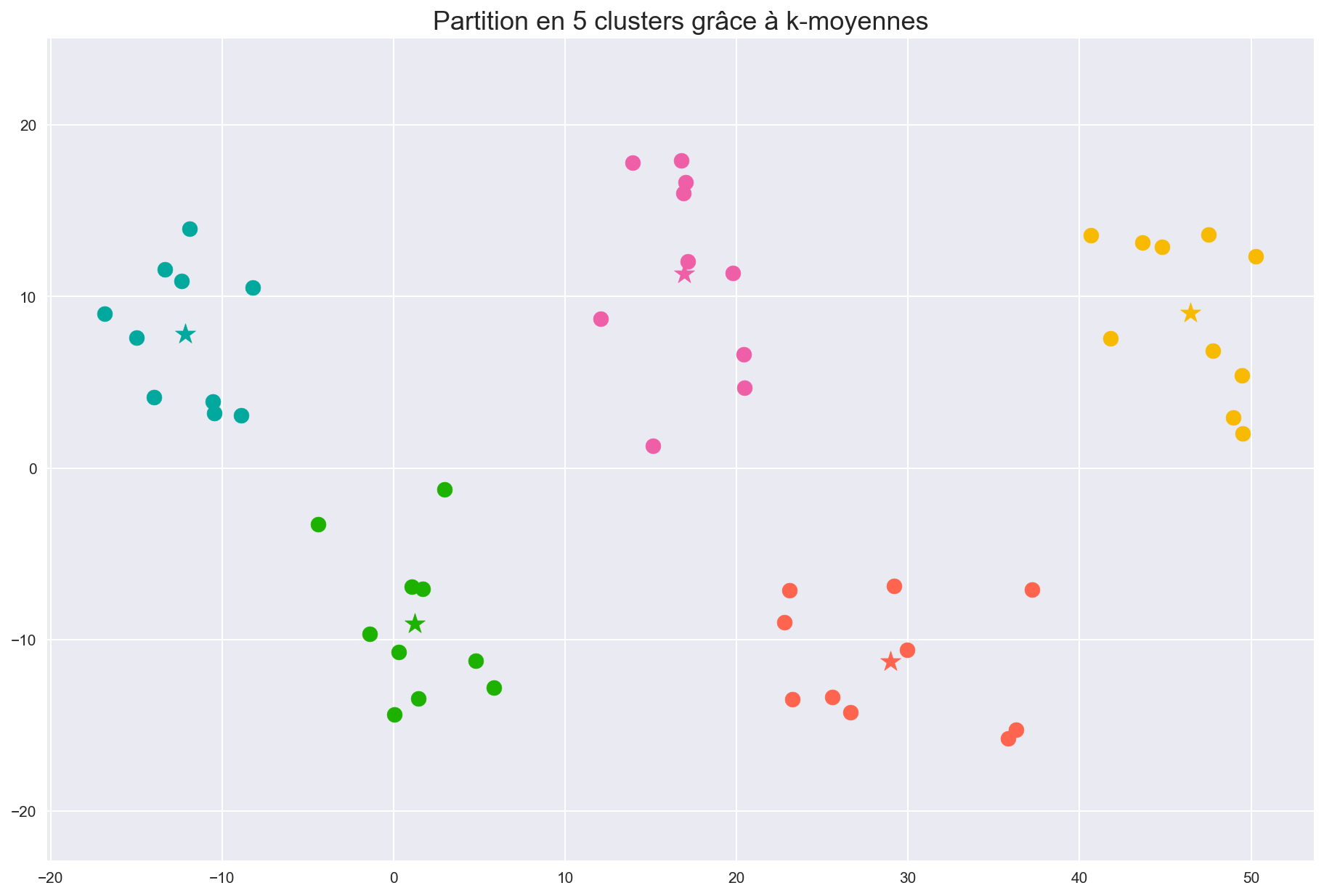
Testons l’algorithme sur des points dispersés artificiellement en 5 groupes.
from random import random
n = 10
X1 = [-15+(random()-0.5)*15 for i in range(n)]
Y1 = [8+(random()-0.5)*12 for i in range(n)]
X2 = [0+(random()-0.5)*12 for i in range(n)]
Y2 = [-7+(random()-0.5)*15 for i in range(n)]
X3 = [15+(random()-0.5)*12 for i in range(n)]
Y3 = [10+(random()-0.5)*18 for i in range(n)]
X4 = [30+(random()-0.5)*15 for i in range(n)]
Y4 = [-10+(random()-0.5)*12 for i in range(n)]
X5 = [45+(random()-0.5)*13 for i in range(n)]
Y5 = [8+(random()-0.5)*12 for i in range(n)]
data = list(zip(X1+X2+X3+X4+X5,Y1+Y2+Y3+Y4+Y5))
fig,ax = plt.subplots()
ax.axis('equal')
ax.scatter(X1+X2+X3+X4+X5,Y1+Y2+Y3+Y4+Y5,s=100)
ax.set_title("Les données")
fig,ax = plt.subplots()
ax.axis('equal')
k = 5
clusters, centres = kmoyennes(k,data)
Couleurs = ["#1DB100","#F8BA00","#EF5FA7","#00A89D","#FF644E"]
for i in range(len(data)):
ax.scatter(*data[i],c=Couleurs[clusters[i]],s=100)
for i in range(k) :
ax.scatter(*centres[i],c=Couleurs[i],s=200,marker='*')
ax.set_title("Partition en 5 clusters grâce à k-moyennes")
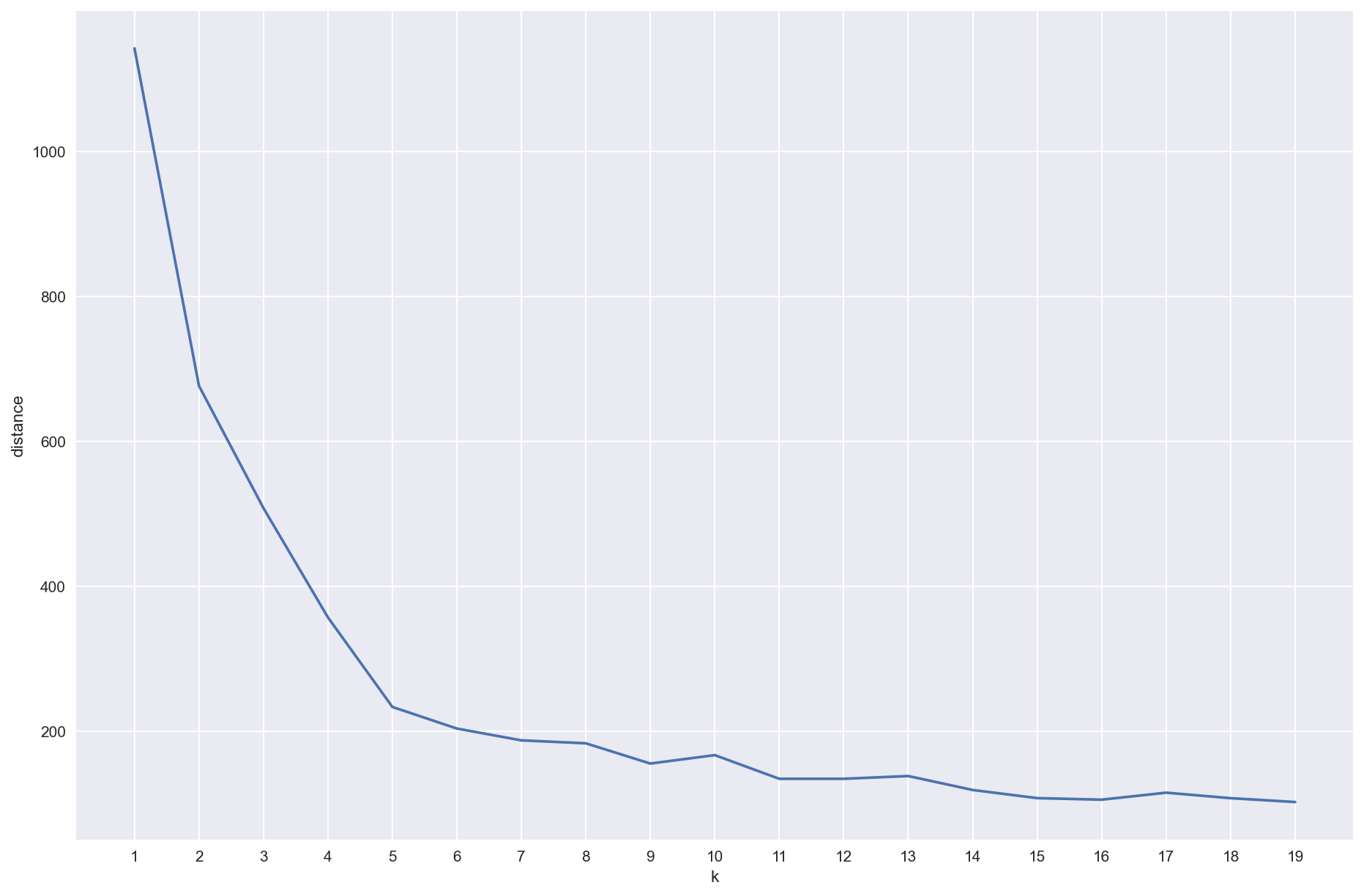
Traçons la courbe représentant la somme des distances entre un centre et les points de son cluster en fonction de k.
K = [i for i in range(1,20)]
V = []
n = len(data)
for k in K:
clusters, centres = kmoyennes(k,data)
v = evaluation(k,clusters,centres,data)
V.append(v)
plt.xticks([k for k in K])
plt.plot(K,V)
plt.xlabel('k')
plt.ylabel('distance')
Si vous passez la valeur de itgenmax à 1 dans le code de kmoyennes, on obtient une courbe bien moins monotone. Le vérifier.
Voyez-vous pourquoi ?
Correction (cliquer pour afficher)
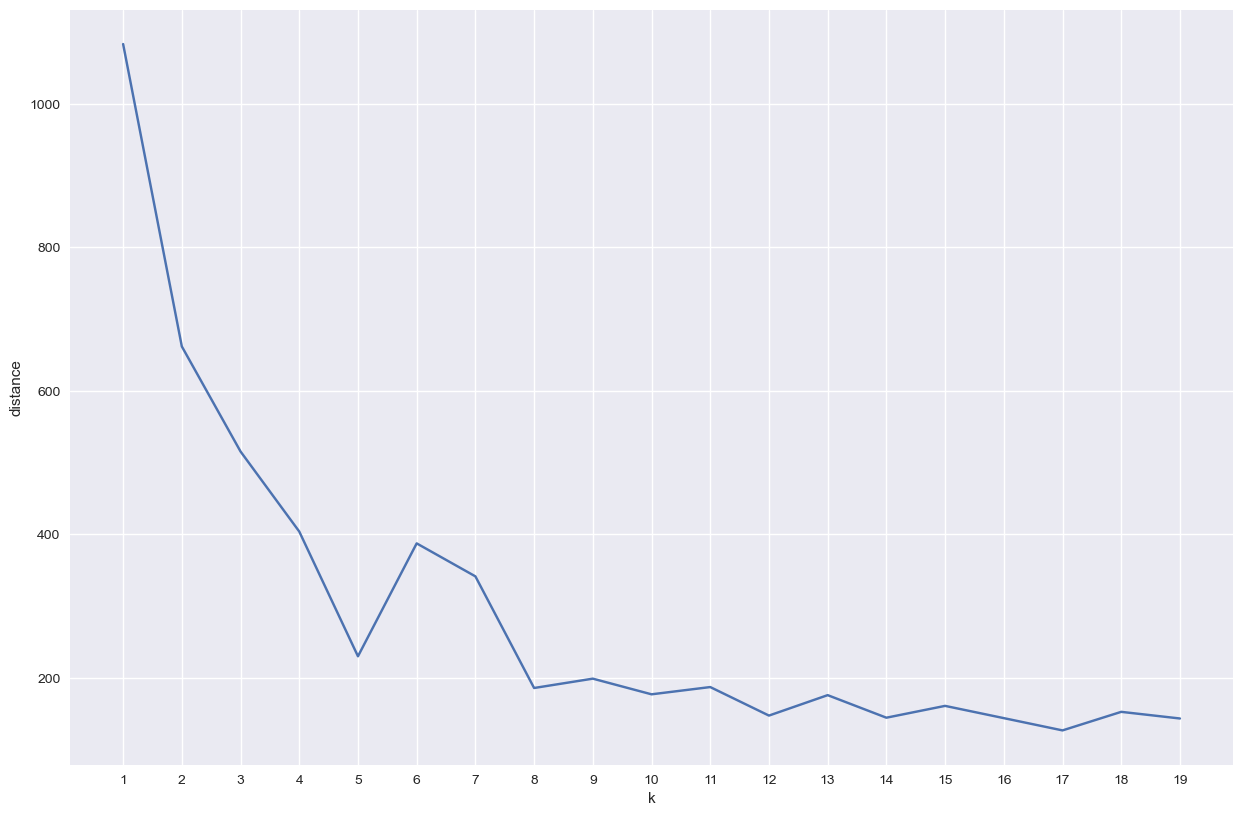
itgenmaxcorrespond au nombre de fois que l'algorithme est relancé sachant qu'au final, on ne garde que la meilleure solution (celle minimisant l'inertie).
Sans répétition, la probabilité, pour un k donné, de se retrouver bloquer sur une solution suboptimale (augmentant l'inertie) est donc bien plus grande.
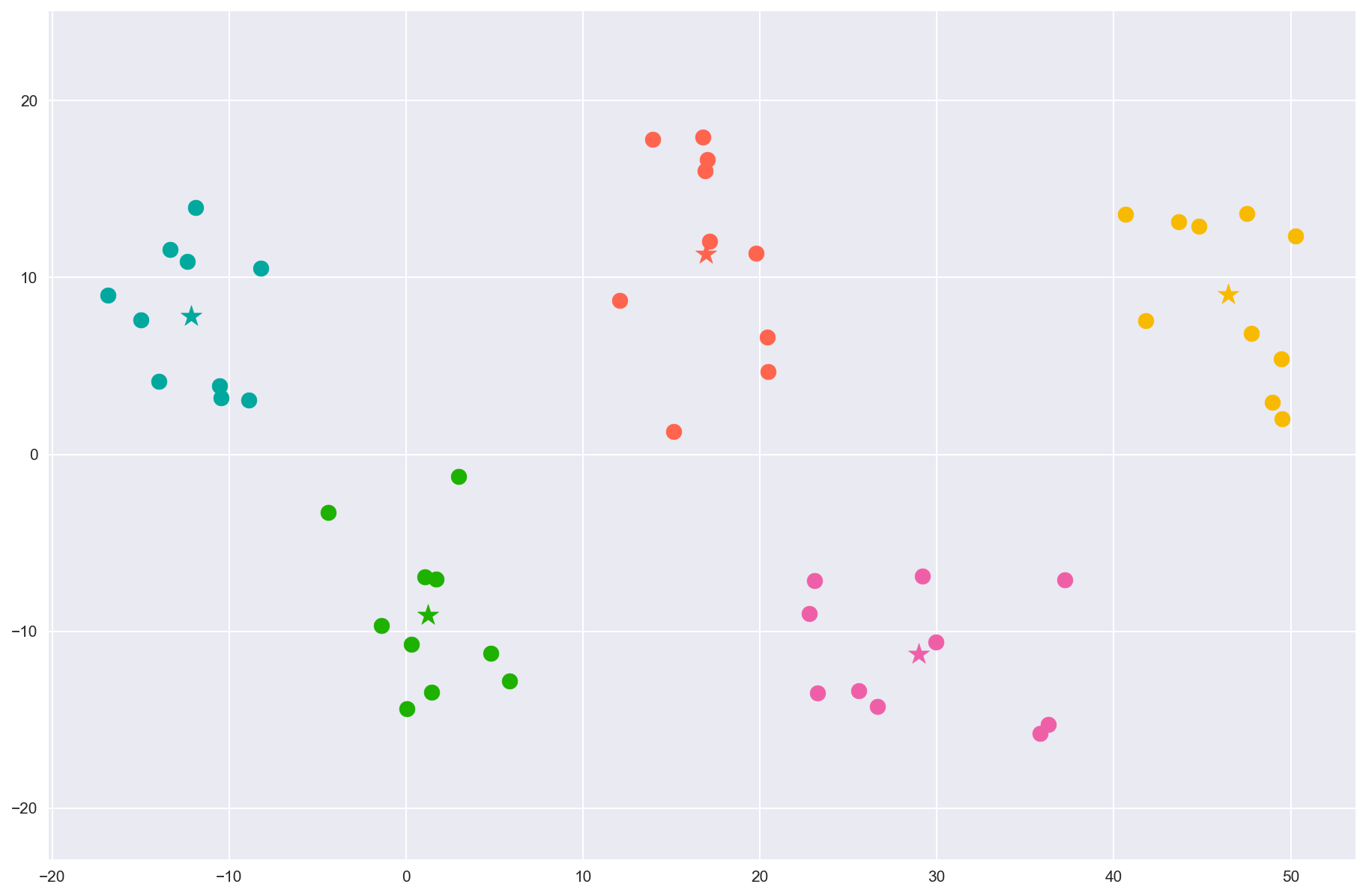
Familiarisons-nous maintenant justement avec l’implémentation de scikit-learn et vérifions qu’elle fait bien le même boulot (mais bien plus vite).
from sklearn.cluster import KMeans
fig,ax = plt.subplots()
ax.axis('equal')
k = 5
kmeans_model = KMeans(n_clusters = k)
cluster_labels = kmeans_model.fit_predict(data) # donne la liste ordonnée du cluster auquel appartient chaque point de données
centres = kmeans_model.cluster_centers_
Couleurs = ["#1DB100","#F8BA00","#EF5FA7","#00A89D","#FF644E"]
for i in range(len(data)) :
ax.scatter(*data[i],c=Couleurs[cluster_labels[i]],s=100)
for i in range(k) :
ax.scatter(*centres[i],c=Couleurs[i],s=200,marker='*')
La grande popularité de Python aujourd’hui dans le monde scientifique et professionnel s’explique en grande partie par ses librairies. En peu de lignes, elles permettent d’obtenir très rapidement des résultats de bonne tenue.
import seaborn as sns
import pandas as pd
import numpy as np
n = 5000
# Simulation des données
x1 = np.random.normal(-4, 0.8, n)
y1 = np.random.normal(-2, 1.2, n)
x2 = np.random.normal(0, 0.9, n)
y2 = np.random.normal(0, 0.9, n)
x3 = np.random.normal(2, 1.2, n)
y3 = np.random.normal(4, 0.5, n)
x4 = np.random.normal(1.5, 0.3, n)
y4 = np.random.normal(-6, 0.3, n)
x5 = np.random.normal(3.5, 0.3, n)
y5 = np.random.normal(-4, 0.4, n)
data = list(zip(np.concatenate((x1,x2,x3,x4,x5)),np.concatenate((y1,y2,y3,y4,y5))))
k = 5
kmeans_model = KMeans(n_clusters = k)
cluster_labels = kmeans_model.fit_predict(data)
centres = kmeans_model.cluster_centers_
df = pd.DataFrame(data,columns=['x','y'])
df['cluster'] = cluster_labels
sns.scatterplot(x='x',y='y',hue='cluster',data=df)
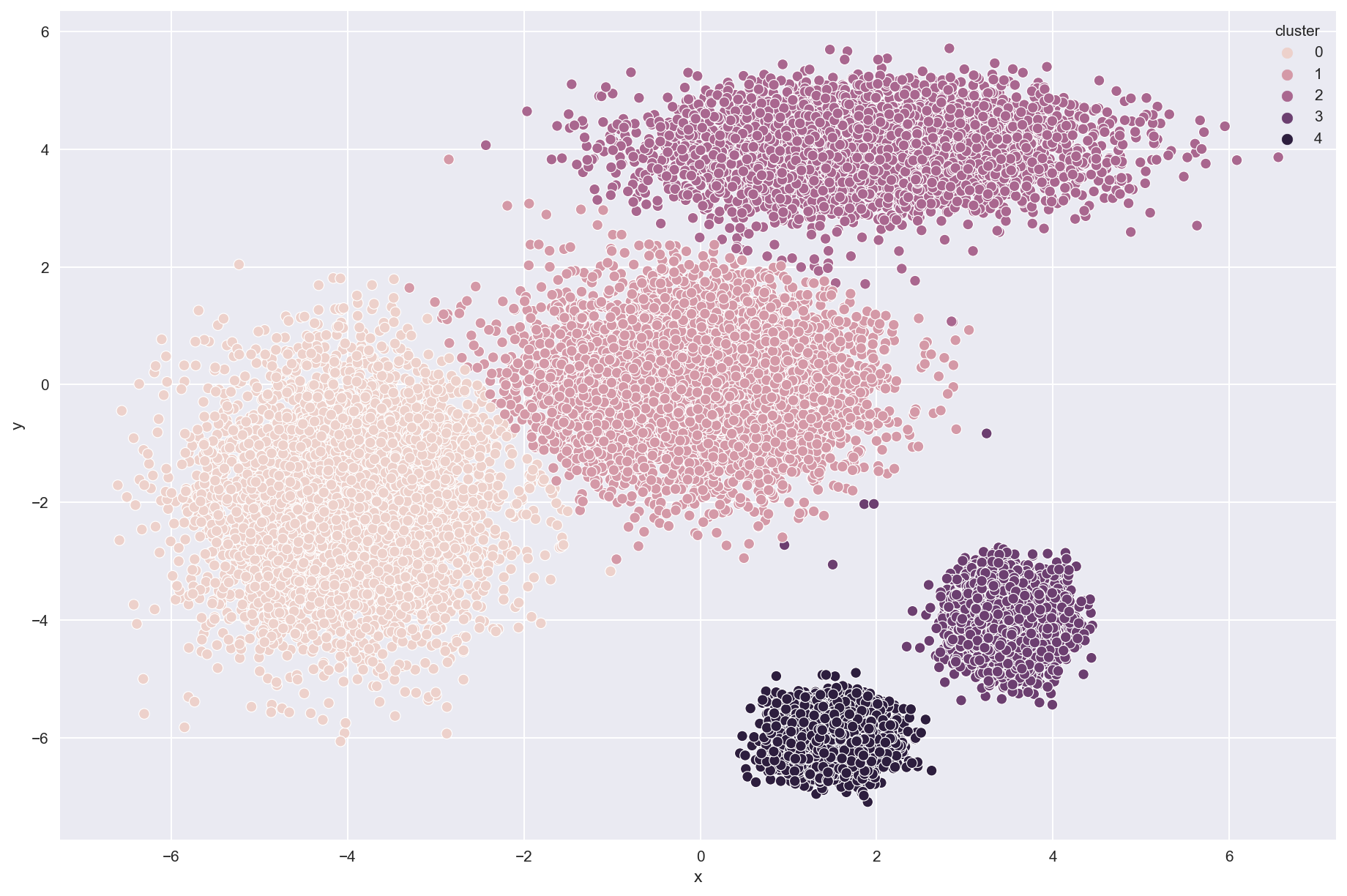
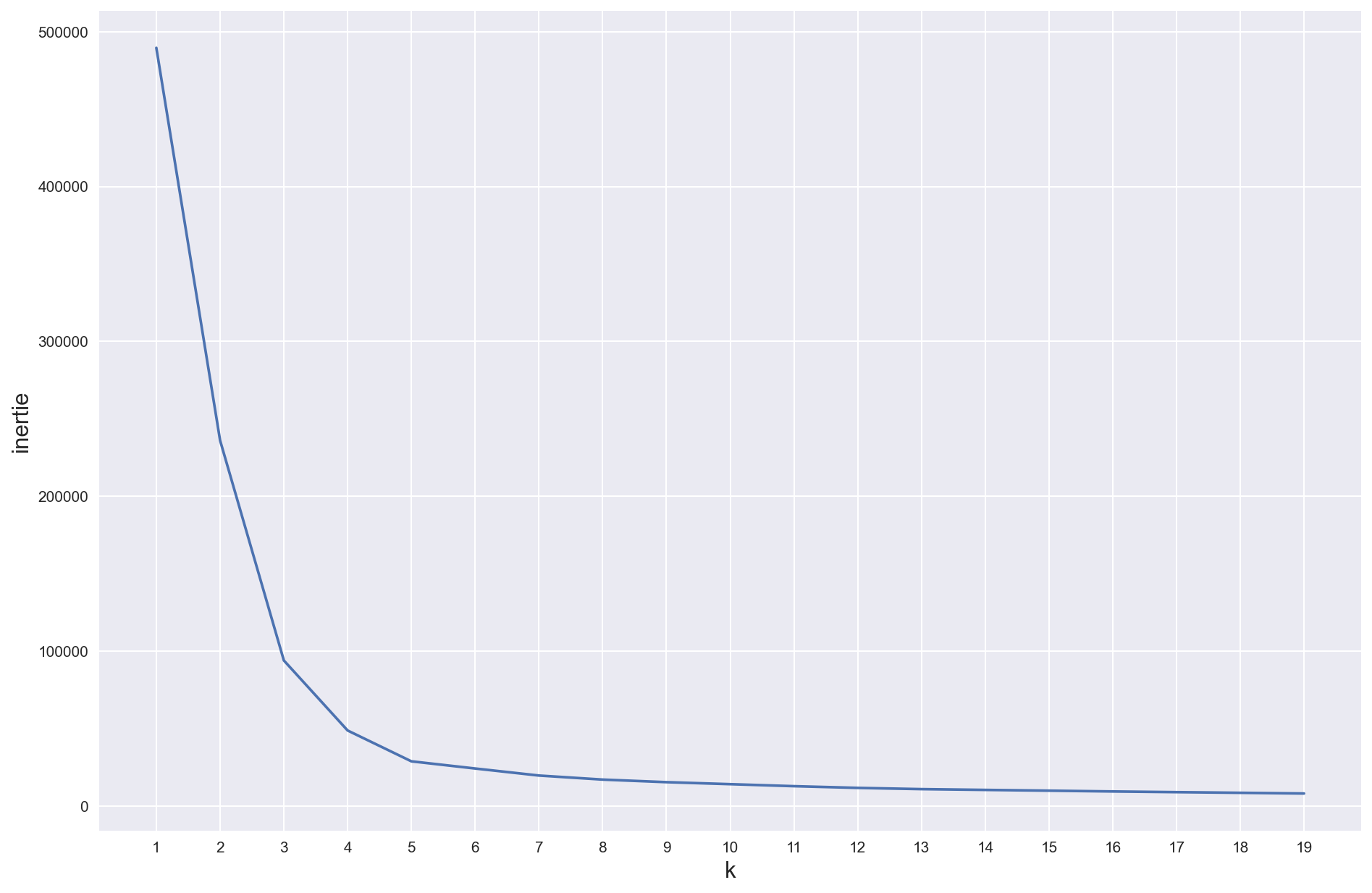
K = [i for i in range(1,20)]
V = []
n = len(data)
for k in K :
kmeans_model = KMeans(n_clusters = k)
kmeans_model.fit_predict(data)
V.append(kmeans_model.inertia_)
plt.xticks([k for k in K])
plt.plot(K,V)
plt.xlabel('k',fontsize=15)
plt.ylabel('inertie',fontsize=15)
Dans un TP du premier semestre, on s’était amusé à downgrader le nombre de couleurs d’une image en passant d’un codage de 24 bits à 6 bits pour la profondeur des couleurs.
On va essayer d’utiliser k-moyennes pour faire un travail ressemblant, mais plus fin : on va chosir un nombre de couleurs et laisser k-moyennes trouver lui-même les couleurs les plus adaptées et créer le partitionnement.
Les couleurs vont être données par les coordonnées des k centres !
Cette opération s’appelle segmentation d’image et il s’agit là plus précisément d’une segmentation par la couleur. C’est une technique utilisée en diagnostique médical ou pour l’analyse d’images satellites (pour déterminer, par exemple, la proportion de forêt dans une région).
from PIL import Image
import urllib.request
from IPython.display import display
import matplotlib.pyplot as plt
import numpy as np
urllib.request.urlretrieve('https://webb.nasa.gov/content/webbLaunch/assets/images/firstImages/image5-StarForming/STSCI-J-p22031a-1100px.jpg', 'webb')
image_webb = np.array(Image.open('webb'))
webb = Image.fromarray(image_webb)
display(webb)
h,l,c = image_webb.shape
print(f'hauteur : {h} px ; largeur : {l} px')

hauteur : 1200 px ; largeur : 1200 px
On transforme d’abord l’image bidimensionnelle en un tableau à une dimension contenant hauteur$\times$largeur triplets. On a ainsi un long vecteur de points tridimensionnels.
Ensuite, on applique l’algorithme (celui de scikit-learn vu le nombre de points) et on récupère les centres.
Rq : mon vieil ordinateur met environ une heure avec l’algo maison…
image_1D = image_webb.reshape(h*l,c)
k = 10
kmeans_model = KMeans(n_clusters = k)
cluster_labels = kmeans_model.fit_predict(image_1D)
centres = kmeans_model.cluster_centers_
print(centres)
[ 65.2464465 40.79341585 42.47060682]
[132.70876194 76.59044699 62.2814825 ]
[186.45279371 137.82358444 113.88598154]
[ 35.02064311 48.64635552 93.31092396]
[ 99.94155291 58.02521904 52.17321541]
[ 89.34394389 119.63315649 172.00437611]
[ 27.29924084 25.17800936 34.18811588]
[209.40854976 195.09625895 200.31127399]
[155.8400736 105.64875463 88.45913989]]
Pour faire passer les coordonnées de ces centres pour des couleurs, on convertit les flottants en entier :
couleurs = kmeans_model.cluster_centers_.round(0).astype(np.uint8)
print(couleurs)
[ 65 41 42]
[133 77 62]
[186 138 114]
[ 35 49 93]
[100 58 52]
[ 89 120 172]
[ 27 25 34]
[209 195 200]
[156 106 88]]
Plus qu’à former l’image finale. numpy permet de faire ça en une ligne…
image_webb_clust = np.reshape(couleurs[cluster_labels],(h,l,c))
webbClus = Image.fromarray(image_webb_clust)
display(webbClus)

Vous allez faire le même travail sur la petite image suivante, mais sans utiliser scikit-learn (on reste avec notre lent kmoyennes) ni numpy (seulement des braves listes python).
image_2D = []
for i in range(64):
image_2D.append([])
for j in range(64):
image_2D[i].append((min(255,64+(i+j)*2),255-i*3,255-j*3))
plt.figure(figsize=(3,3))
plt.imshow(image_2D)
plt.axis('off')
image_1D = []
for i in range(64):
for j in range(64):
image_1D.append(image_2D[i][j])

Vous devez obtenir une liste bidimensionnelle contenant les valeurs des pixels de l’image segmentée en 8.
Vous appelerez cette listeimage_2D_seg4.
À la suite de votre cellule réponse, vous pourrez tester votre liste en affichant l’image qu’elle contient. Si vous obtenez 8 partitions, c’est gagner (n’hésitez pas à relancer l’algo car il peut se bloquer sur un découpage suboptimal contenant moins de parties).
Correction (cliquer pour afficher)
k = 8 clusters,centres = kmoyennes(k,image_1D) for i in range(k): for j in range(3): centres[i][j] = int(centres[i][j]) for i in range(len(image_1D)): image_1D[i] = centres[clusters[i]] image_2D_seg4 = [] i1D = 0 for i in range(64): image_2D_seg4.append([]) for j in range(64): image_2D_seg4[i].append(image_1D[i1D]) i1D += 1
Jeux d’accessibilité à deux joueurs
La démonstration du cours sur les graphes bipartis donne une idée d’algorithme pour les détecter si le graphe est non orienté :
- on explore un graphe en partant d’un sommet grâce au parcours en largeur qui progrese couche par couche,
- on dresse un inventaire des distances entre le sommet de départ et les sommets explorés grâce à un dictionnaire,
- à chaque ajout d’un sommet à la file, on enregistre sa distance dans le dictionnaire en ajoutant 1 à la distance de son prédécesseur.
Pour prouver qu’un graphe n’est pas biparti, il suffit de trouver au moins un cycle de longueur impair. Or la présence d’un tel cycle impose de tomber sur un sommet déjà exploré avec la même distance au sommet de départ que son prédécesseur (s’il n’y a pas de cycle impair, cela n’arrive jamais).
Compléter la fonction suivante pour qu’elle retourne vrai si le graphe est biparti et faux sinon.
from collections import deque
def testBipartite(G,depart):
"""
precondition: le graphe G doit être non orienté
postconditions: le dictionnaire Vus dit si un sommet a été exploré ou non
le dictionnaire Distance donne la distance de chaque sommet ajouté par rapport au sommet de départ
la fonction retourne Vrai si on tombe sur un sommet déjà exploré
dont la distance au sommet de départ est la même que celle de son prédécesseur
et Faux si aucun tel cas n'est rencontré.
"""
Vus = {s : False for s in G}
Distance = {s : 0 for s in G}
file = deque()
file.append(depart)
# VOTRE CODE
Correction (cliquer pour afficher)
def testBipartite(G,depart): Vus = {s : False for s in G} Distance = {s : 0 for s in G} file = deque() file.append(depart) while file: sommet = file.popleft() if not Vus[sommet]: Vus[sommet] = True for s in G[sommet]: if Vus[s]: if Distance[s] == Distance[sommet]: return False Distance[s] = Distance[sommet] + 1 file.append(s) return True
# Deux graphes pour tester votre algorithme
Ga = {'A': ['B','E'],
'B': ['A','C','D','F'],
'C': ['B'],
'D': ['B'],
'E': ['A','F'],
'F': ['B','E']
}
Gb = {'A': ['B','E'],
'B': ['A','C','D','E','F'],
'C': ['B'],
'D': ['B'],
'E': ['A','B','F'],
'F': ['B','E']
}
Le graphe suivant est-il bipati ?
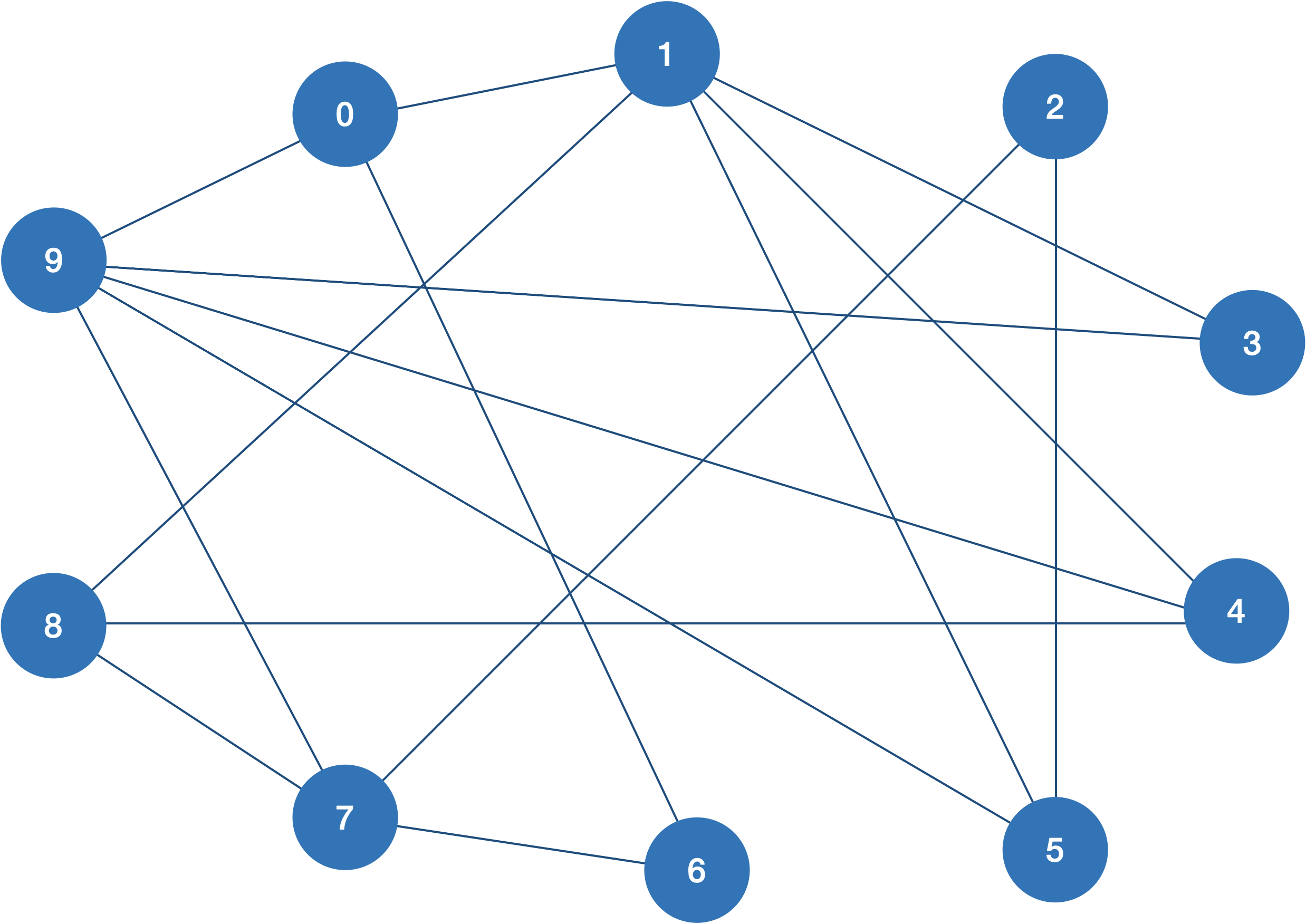
Correction (cliquer pour afficher)
AppelonsGcle graphe dessiné.Gc = {0:[1,6,8,9], 1:[0,3,4,5], 2:[3,5,7], 3:[1,2,9], 4:[1,8,9], 5:[1,2,9], 6:[0,7], 7:[2,6,8,9], 8:[0,4,7], 9:[0,3,4,5,7], } print(testBipartite(Ga,'A')) print(testBipartite(Gb,'A')) print(testBipartite(Gc,1))True
False
True
On peut prouver queGaetGcsont bipartis en les 2-coloriant (il ne faut pas que 2 sommets adjacents aient la même couleur) alors que c'est impossible pourGb: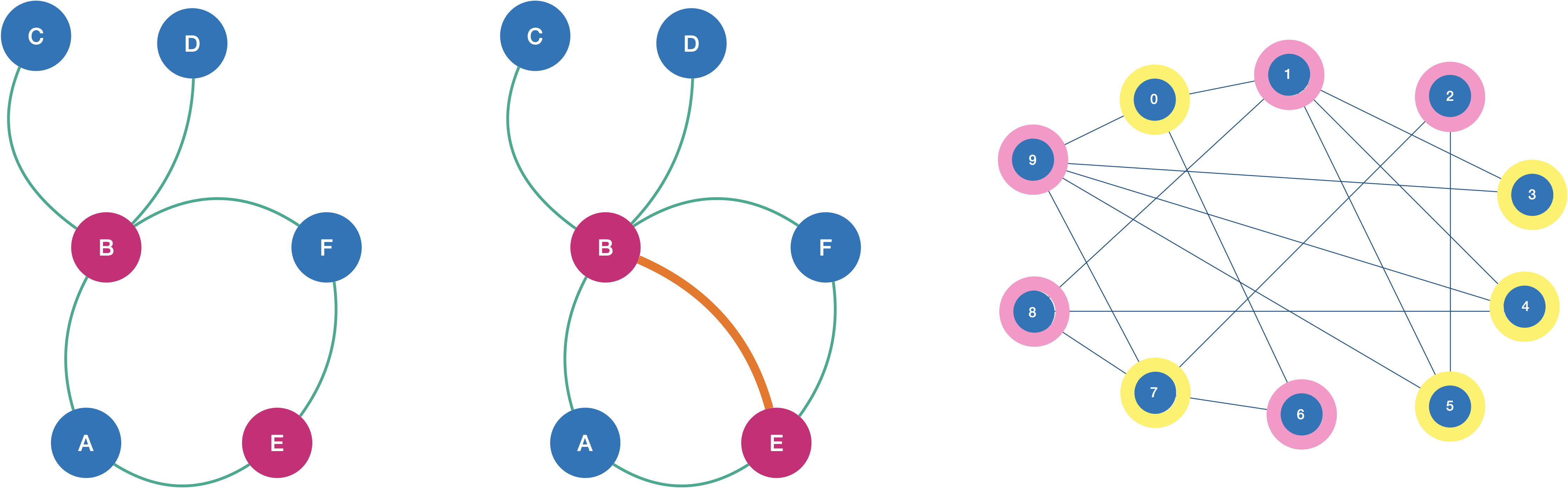
Revenons maintenant sur la variante du jeu de Nim présenté dans le cours.
Commentaire (cliquer pour afficher)
Ce notebook Colab reprend et détaille la partie qui suit du TP.
Construire le graphe correspondant à un paquet de 10 allumettes au départ.
Vous appelerez ce grapheG1.
Correction (cliquer pour afficher)
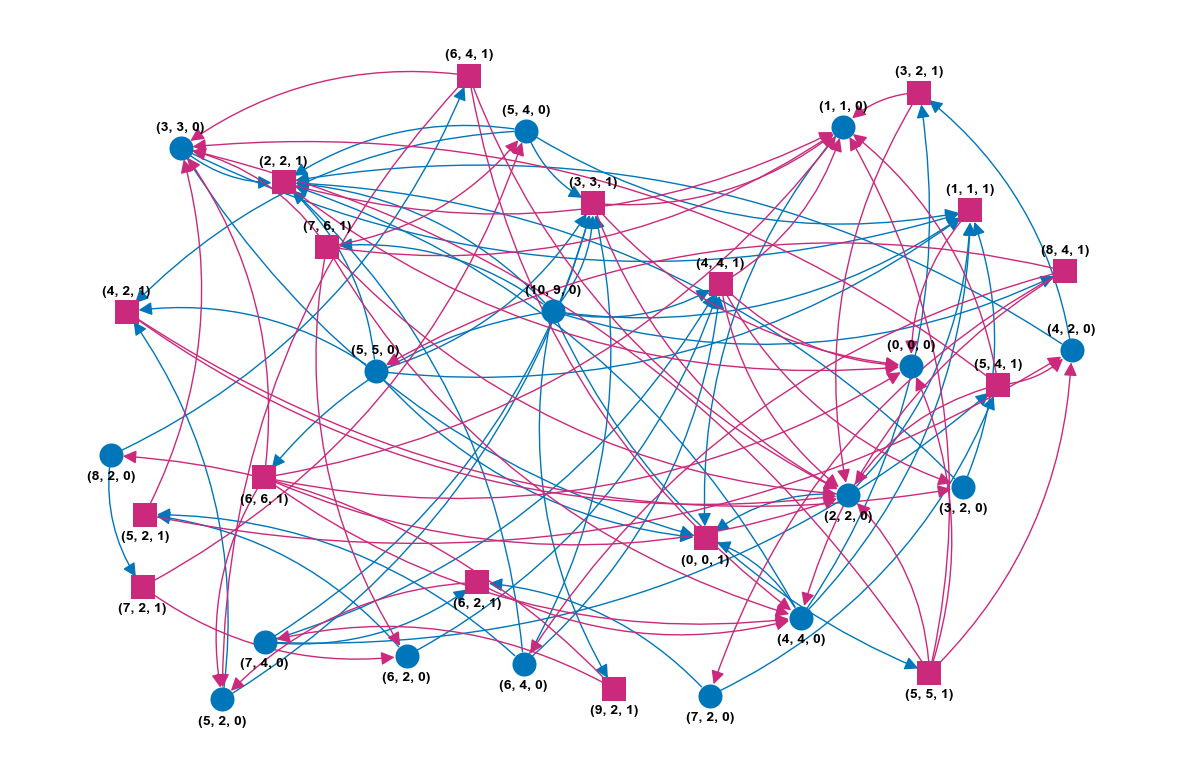
La construction suivante est récursive : pour chaque sommet, on construit la liste de ses successeurs puis on appelle la fonction sur chacun d'eux. Le cas de base correspond à l'absence de successeur possible.Depart = (10,9,0) # 0 pour Eve def constrG(S,G): G[S] = [] if S[0] == 0: return i = 1 while i <= S[1] and S[0]-i >= 0: if 2*i < S[0]-i: nvSommet = (S[0]-i,2*i,(1+S[2])%2) else: nvSommet = (S[0]-i,S[0]-i,(1+S[2])%2) G[S].append(nvSommet) i += 1 for s in G[S]: constrG(s,G) G1 = {} constrG(Depart,G1)
Eve est représentée par les ronds bleus dans la représentation suivante.
import networkx as nx
import matplotlib.pyplot as plt
g = nx.DiGraph(G1)
edge_colors = ['#0076BA' if e[0][2]==0 else '#CB297B' for e in g.edges]
Eve_nodes = [s for s in g.nodes if s[2]==0]
Adam_nodes = list(set(g.nodes) - set(Eve_nodes))
Eve_edges = [e for e in g.edges if e[0][2]==0]
Adam_edges = list(set(g.edges) - set(Eve_edges))
pos = nx.spring_layout(g,k=1,iterations=5)
shift = 0.06
pos_higher = {k:(v[0],v[1]+shift) if v[1]>0 else (v[0],v[1]-shift*1.1) for k,v in pos.items()}
fig, ax = plt.subplots(figsize=(15,10))
nx.draw_networkx_nodes(g, pos, nodelist=Eve_nodes, node_color='#0076BA', node_shape='o', linewidths=0)
nx.draw_networkx_nodes(g, pos, nodelist=Adam_nodes, node_color='#CB297B', node_shape='s', linewidths=0)
nx.draw_networkx_edges(g, pos, edgelist=Eve_edges, edge_color='#0076BA', arrows=True, arrowsize=20, connectionstyle='arc3,rad=0.2')
nx.draw_networkx_edges(g, pos, edgelist=Adam_edges, edge_color='#CB297B', arrows=True, arrowsize=20, connectionstyle='arc3,rad=0.2')
nx.draw_networkx_labels(g, pos = pos_higher, font_color='#000000', font_size=10, font_weight='bold')
ax.set_facecolor('w')
ax.axis('off')
plt.show()
Reprenons le code du cours visant à assembler l’attracteur du jeu pour Eve.
def attracteur(G: dict, F: list) -> list:
"""
préconditions: G est est un graphe sous forme de liste d'adjacence implémentée par un dictionnaire
F est la liste des sommets gagnants pour le joueur 1
postcondition: la fonction retourne l'attracteur de F pour le joueur 1 sous forme d'un dictionnaire
dont les clés sont les sommets de G et les valeurs True ou False suivant que le sommet appartienne ou non à l'attracteur
"""
Pred = inverseGraphe(G)
n = {s:len(G[s]) for s in G}
Attr = {s:False for s in G}
for sommet in F:
Joueur1 = True
propage(sommet,Joueur1,Attr,Pred,n)
return Attr
def propage(sommet,Joueur1,Attr,Pred,n):
if Attr[sommet]:
return
Attr[sommet] = True
for s in Pred[sommet]:
n[s] -= 1
if Joueur1 or (n[s] == 0):
propage(s,not Joueur1,Attr,Pred,n)
Il manque la définition de la fonction
inverseGraphequi retourne la liste d’adjacence du graphe G dont on aurait inversé chacun des arcs.
À vous de jouer…
def inverseGraphe(G: dict) -> dict:
"""
précondition: G est la liste d'adjacence (sous forme de dictionnaire) d'un graphe orienté
"""
# VOTRE CODE
Correction (cliquer pour afficher)
def inverseGraphe(G): inv = {s:[] for s in G} for pred in G: for succ in G[pred]: inv[succ].append(pred) return inv
Fabriquons l’attracteur de G1.
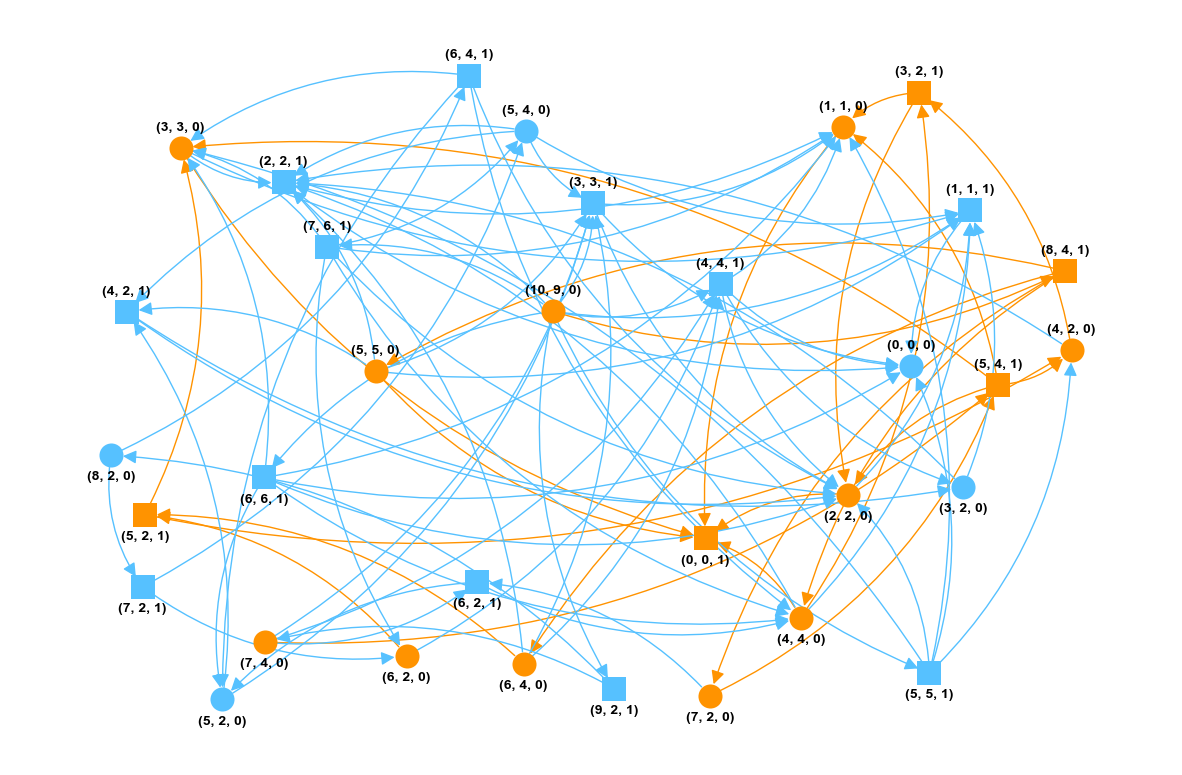
Attr = attracteur(G1,[(0,0,1)])
Dans la représentation ci-dessous, l’attracteur est en orange.
g = nx.DiGraph(G1)
Eve_nodes = [s for s in g.nodes if s[2]==0]
Eve_Attr_nodes = [s for s in Eve_nodes if Attr[s]==True]
Eve_piege_nodes = list(set(Eve_nodes) - set(Eve_Attr_nodes))
Adam_nodes = list(set(g.nodes) - set(Eve_nodes))
Adam_attr_nodes = [s for s in Adam_nodes if Attr[s]==True]
Adam_piege_nodes = list(set(Adam_nodes) - set(Adam_attr_nodes))
Attr_edges = [e for e in g.edges if Attr[e[0]]==True and Attr[e[1]]==True]
Piege_edges = list(set(g.edges) - set(Attr_edges))
fig, ax = plt.subplots(figsize=(15,10))
nx.draw_networkx_nodes(g, pos, nodelist=Eve_piege_nodes, node_color='#56C1FF', node_shape='o', linewidths=0)
nx.draw_networkx_nodes(g, pos, nodelist=Eve_Attr_nodes, node_color='#FF9300', node_shape='o', linewidths=0)
nx.draw_networkx_nodes(g, pos, nodelist=Adam_piege_nodes, node_color='#56C1FF', node_shape='s', linewidths=0)
nx.draw_networkx_nodes(g, pos, nodelist=Adam_attr_nodes, node_color='#FF9300', node_shape='s', linewidths=0)
nx.draw_networkx_edges(g, pos, edgelist=Attr_edges, edge_color='#FF9300', arrows=True, arrowsize=20, connectionstyle='arc3,rad=0.2')
nx.draw_networkx_edges(g, pos, edgelist=Piege_edges, edge_color='#56C1FF', arrows=True, arrowsize=20, connectionstyle='arc3,rad=0.2')
nx.draw_networkx_labels(g, pos = pos_higher, font_color='#000000', font_size=10, font_weight='bold')
ax.set_facecolor('w')
ax.axis('off')
plt.show()
def strategie(G,depart,F,attracteur):
Joueur1 = True
if not attracteur[depart]:
print("Pas de stratégie gagnante possible pour le joueur1 depuis cet endroit :(")
return False
S = depart
while S not in F:
if Joueur1:
for s in G[S]:
if attracteur[s]:
print(f"Coup gagnant : {s}.")
S = s
break
else:
print("Qu'a joué l'adversaire ?")
for i,s in enumerate(G[S],1):
print(f"{i} : {s}")
S = G[S][int(input("Choisir : "))-1]
Joueur1 = not Joueur1
print("C'est gagné !")
En utilisant le programme ci-dessus, répondre à la question suivante :
si Adam joue (6,4,0) à son premier coup, sur quel sommet doit se déplacer Eve pour continuer à avoir l’avantage ?
Correction (cliquer pour afficher)
(5,2,1)
Créez un graphe
G2pour répondre à cette question :
La position de départ $(21,5,0)$ est-elle gagnante ?
Correction (cliquer pour afficher)
S'affiche alors :G2 = {} constrG((21,5,0),G2) strategie(G2,(21,5,0),[(0,0,1)],attracteur(G2,[(0,0,1)]))
Pas de stratégie gagnante possible pour le joueur1 depuis cet endroit :(
Rq : on peut montrer que le joueur 1 aura toujours une stratégie gagnante si la position de départ (le nombre initial d’allumettes) ne se trouve pas dans la suite de Fibonacci.
Passons maintenant au vrai jeu de Nim, dans sa variante misère, popularisé dans le film d’Alain Resnais “L’Année dernière à Marienbad”.
 On a 4 tas composés au départ de 1, 3, 5 et 7 allumettes. Chaque joueur peut, l’un après l’autre, prendre autant d’allumettes qu’il le veut, mais dans un tas seulement.
On a 4 tas composés au départ de 1, 3, 5 et 7 allumettes. Chaque joueur peut, l’un après l’autre, prendre autant d’allumettes qu’il le veut, mais dans un tas seulement.
La variante misère impose que celui qui prend la dernière allumette ait perdu !
Composez le graphe du jeu que vous appelerez
G3. Chaque sommet prendra la forme d’un tuple de 5 entiers (les 4 premiers correspondent aux nombres d’allumettes dans les 4 tas et le 5e est le numéro du joueur (0 pour Eve et 1 pour Adam).
La position de départ est alors(1,3,5,7,0).
La position de départ est-elle gagnante pour le joueur 1 (Eve) ?
Correction (cliquer pour afficher)
def suivantsPossibles(sommet): t1,t2,t3,t4,joueur = sommet Suivants = [] for i in range(t1): Suivants.append((i,t2,t3,t4,(1+joueur)%2)) for i in range(t2): Suivants.append((t1,i,t3,t4,(1+joueur)%2)) for i in range(t3): Suivants.append((t1,t2,i,t4,(1+joueur)%2)) for i in range(t4): Suivants.append((t1,t2,t3,i,(1+joueur)%2)) return SuivantsDans la variante misère, les positions gagnantes pour Eve correspondent à une allumette restante sur une des rangées lorsque c'est au tour d'Adam :G3 = {} def constG(depart,G): S = depart Suivants = suivantsPossibles(S) G[S] = Suivants if len(Suivants) == 0: return else: for s in Suivants: if s not in G: constG(s,G) constG((1,3,5,7,0),G3)
F = [(1,0,0,0,1),(0,1,0,0,1),(0,0,1,0,1),(0,0,0,1,1)]
strategie(G3, (1,3,5,7,0), F, attracteur(G3,F))nous apprend alors que c'est peine perdue de vouloir commencer. Même chose pour la variante classique (où le gagnant est celui qui prend les derniers jetons) comme nous montre cette implémentation javascript, si vous commencez, vous allez perdre.
La vidéo ci-dessous présente plus généralements les jeux de Nim. Ils ont la particularité d’avoir une stratégie (due à M. Bouton) ne nécessitant pas le parcours du graphe théoriquement généralisable à tout jeu impartial.
Occupons-nous enfin du problème du sac-à-dos.
Commentaire (cliquer pour afficher)
À nouveau, un notebook Colab explore cette dernière partie.
Dans le code du cours, il manque à nouveau la définition d’une fonction : sacadosGlouton.
À vous de construire cette fonction qui donne la valeur du sac en suivant la logique gloutonne (et on s’arrêtera au premier objet qui fait dépasser la capacité du sac).
def sacadosGlouton(v: list,p: list,c: int) -> int:
### VOTRE CODE
Correction (cliquer pour afficher)
def sacadosGlouton(v,p,c): n = len(v) ratio = [] valeur, poids = 0, 0 for i in range(n): ratio.append((v[i]/p[i],v[i],p[i])) ratio.sort(reverse=True) for r,val,poi in ratio: if poids + poi >= c: return valeur valeur += val poids += poi
Utiliser ensuite votre fonction et le code du cours pour déterminer la valeur du sac si $v=[1,2,\ldots,200]$, $p=[400,298,296,\ldots,2]$ et $c=156$ (ce nombre d’objets rend la méthode par force brute totalement inutile).
Correction (cliquer pour afficher)
def sacadosBB(v,p,c,i,valeur,poids,meilleure,potentiel): global nbappels nbappels += 1 n = len(v) meilleure = max(meilleure,valeur) if i == n: if poids > c: return 0 else: return valeur elif valeur + potentiel[i] < meilleure: return valeur else: valeurAvec = valeur + v[i] poidsAvec = poids + p[i] sol = sacadosBB_sol(v,p,c,i+1,valeur,poids,meilleure,potentiel) if poidsAvec <= c: sol = max(sol,sacadosBB_sol(v,p,c,i+1,valeurAvec,poidsAvec,meilleure,potentiel)) return solOn obtient ainsi $2334$ (l'algorithme glouton avait, lui, trouvé $2145$, ce qui n'est pas loin du tout et permet donc d'élaguer une grosse partie de l'arbre !).v = [i for i in range(1,201)] p = [2*i for i in range(200,0,-1)] c = 156 nbappels = 0 print(sacadosBB(v,p,c,0,0,0,meilleure,potentiel))
Déterminez aussi (grâce à une variable globale) le nombre d’appels récursifs passés.
Correction (cliquer pour afficher)
print(nbappels) nous donne 64317, ce qui n'est vraiment pas énorme comparé au nombre d'appels qu'il faudrait à l'algo sans élagage.